4.5 Теорема сложения ускорений

Возьмем производную по времени от векторного равенства (4.11), зная, что постоянными являются только вектора по правилам высшей математики.

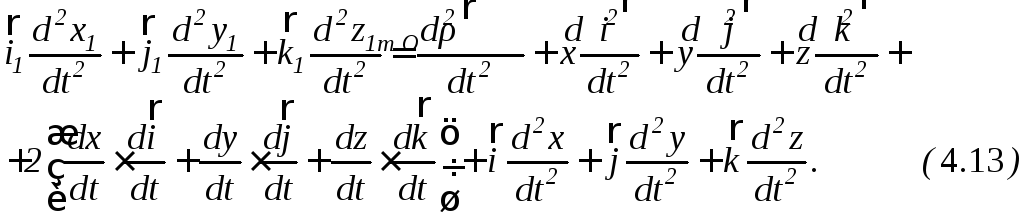
Сравнив слагаемые, входящие в формулу (4.13) с формулами (4.5), (4.7), (4.9), видим, что только выражение не имеет названия. Его называютКориолисовым или поворотным ускорением; названо в честь французского механика Гюстава Гаспара Кориолиса (1792–1843 гг.), который в 1833 г. вывел теорему сложения ускорений ^*). Итак, ускорение Кориолиса равно:

. (4.14)

Векторное равенство (4.13), учитывая названия входящих в него слагаемых, согласно формулам (4.5), (4.7), (4.9), (4.14), имеет вид:

. (4.15)

Эта формула выражает теорему Кориолиса о сложении ускорений.

Абсолютное ускорение точки, совершающей сложное движение, равняется геометрической сумме ее переносного, относительного и Кориолисового ускорений.

Рассмотрим случай, когда переносное движение поступательное. Тогда оси не меняют свою ориентацию (рис. 4.3), можно их выбрать так, что они остаются параллельными осям. В этом случае ускорение Кориолиса равно нулю, т. к.в формуле (4.14).

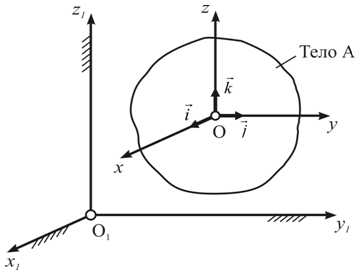
Рисунок 4.3

Теорема сложения ускорений при переносном поступательном движении формулируется так: при переносном поступательном движении абсолютное ускорение точки равно геометрической сумме двух ускорений: переносного и относительного

. (4.16)

4.6 Ускорение Кориолиса и его физический смысл

В предыдущем пункте для ускорения Кориолиса получено выражение (4.14)

.

Для практического вычисления ускорения Кориолиса выполним некоторые преобразования. Так как вектора изменяются только по направлению, рассмотрим частный случай, когдапереносное движение – вращательное вокруг оси с угловой скоростью . Осисвязаны с телом (рис. 4.4).

Изучим, чему равна производная от орта , т. е.. Векторможно рассматривать как радиус-вектор точкиА, т. е. есть скорость точкиA.

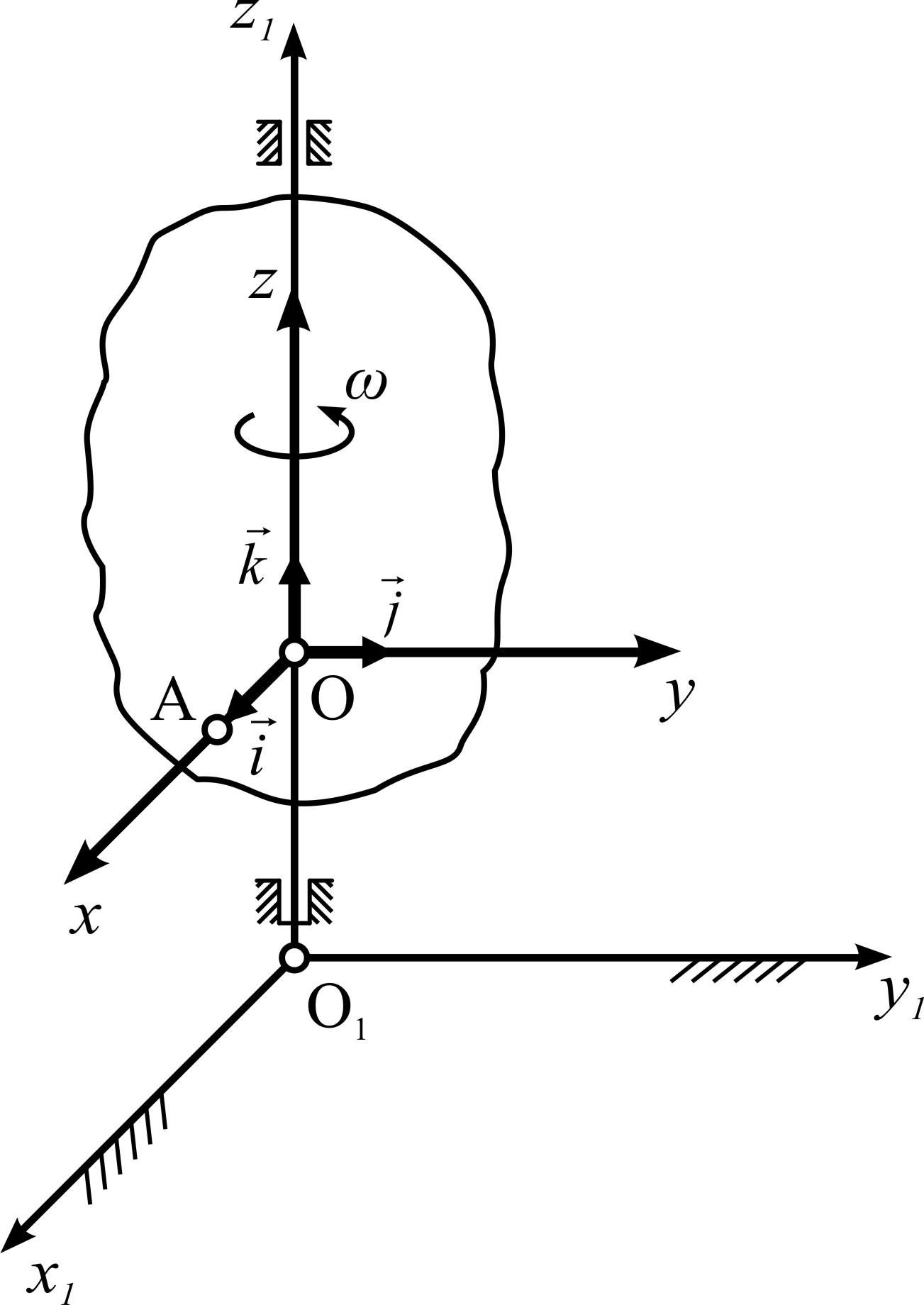
Рисунок 4.4

Применив формулу Эйлера (2.16), имеем скорость точки А: , т.е.. Аналогично, можно убедиться в том, что производная от ортабудет равна. Если ось вращенияне совпадает с неподвижной осью, а тоже движется, то можно убедиться в том, что.

Подставив значения производных от единичных векторов в формулу (4.14), получим . Скобка, стоящая в этой формуле, – это относительная скорость (формула (4.4)). Поэтому

. (4.17)

Вектор ускорения Кориолиса геометрически равняется удвоенному векторному произведению вектора переносной угловой скорости на вектор относительной скорости точки.

Эта формула дает возможность определить как модуль, так и направление ускорения Кориолиса. Исходя из свойств векторного произведения, имеем:

1) модуль ускорения Кориолиса равен:

. (4.18)

2) вектор ускорения направлен перпендикулярно плоскости, в которой расположены вектораи в сторону, откуда поворот вектора к вектору по меньшему углу (чтобы их совместить) видим против хода часовой стрелки (рис. 4.5).

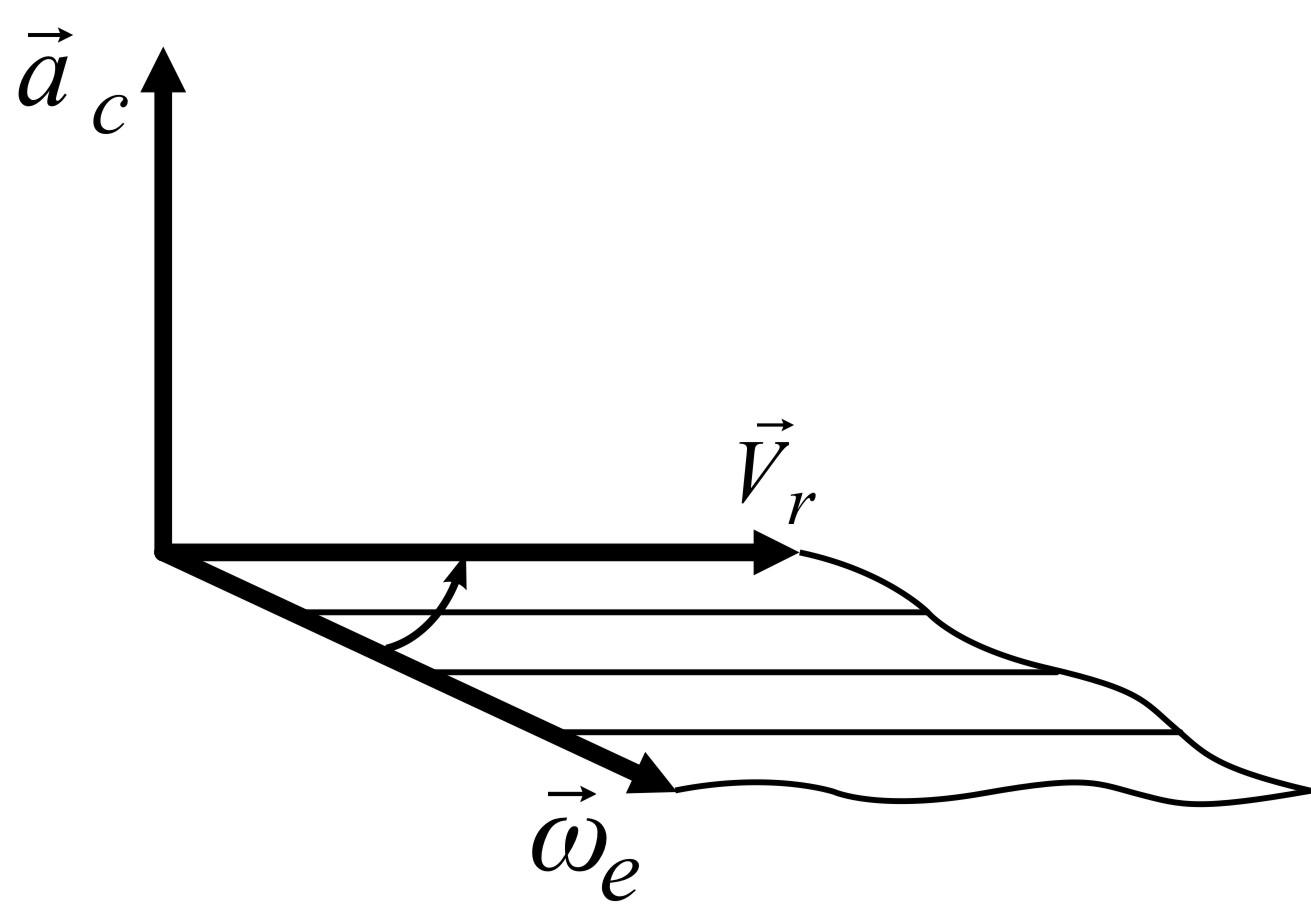
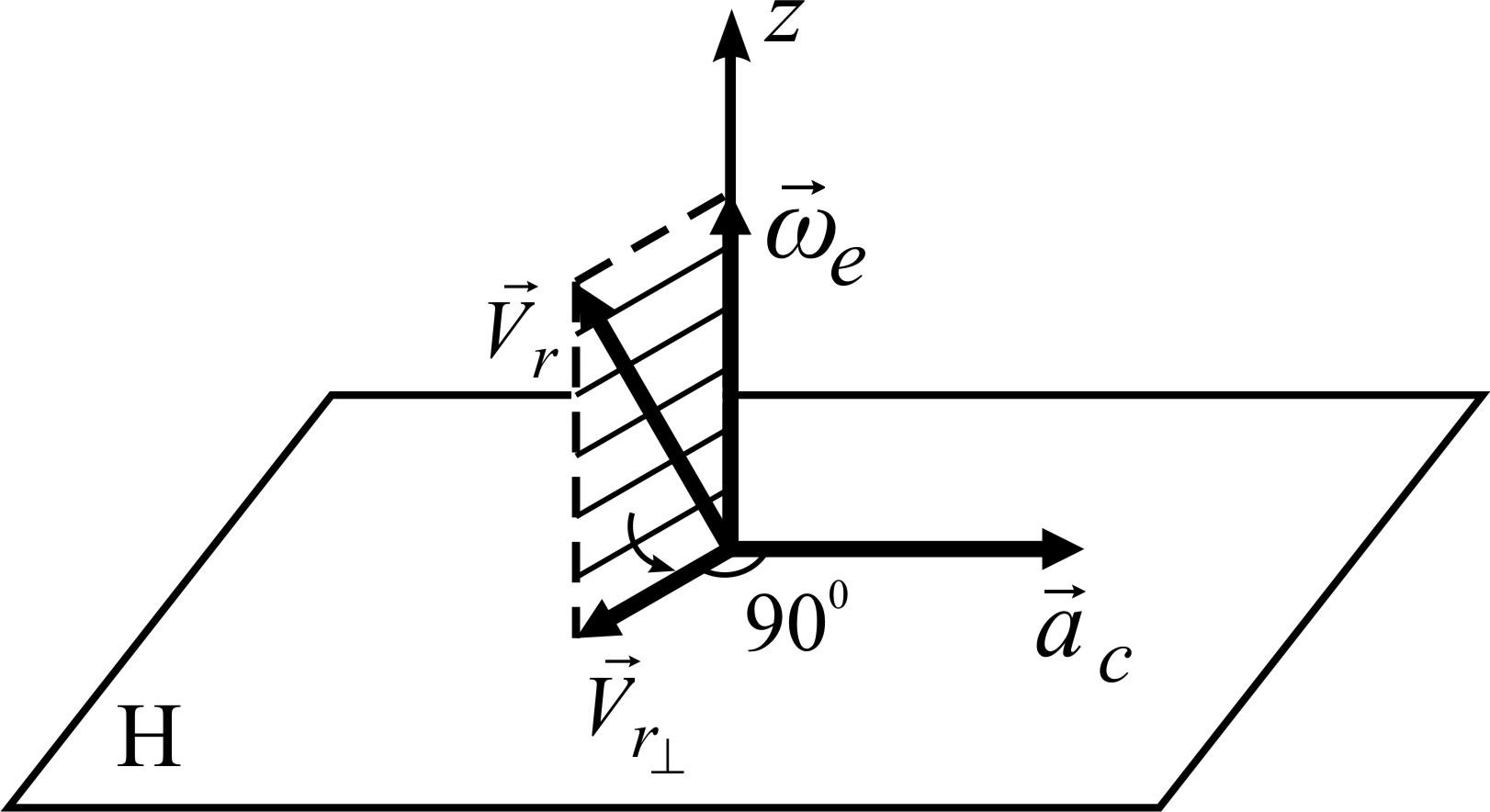
Направление вектора ускорения Кориолиса можно определять по правилу Н. Е. Жуковского^). Для этого необходимо вектор относительной скорости (рис. 4.6) спроецировать на плоскость H, перпендикулярную к оси переносного вращения и полученную проекцию в плоскостиH повернуть на угол 90° в сторону переносного вращения. Это продемонстрировано на рисунке 4.6.

Рисунок 4.5

Рисунок 4.6

Для выяснения физического смысла ускорения Кориолиса рассмотрим такой пример. Диск вращается вокруг оси , перпендикулярной к плоскости диска с постоянной угловой скоростью(рис. 4.7,а). По диску от его центра к ободу с постоянной скоростью движется точка M.

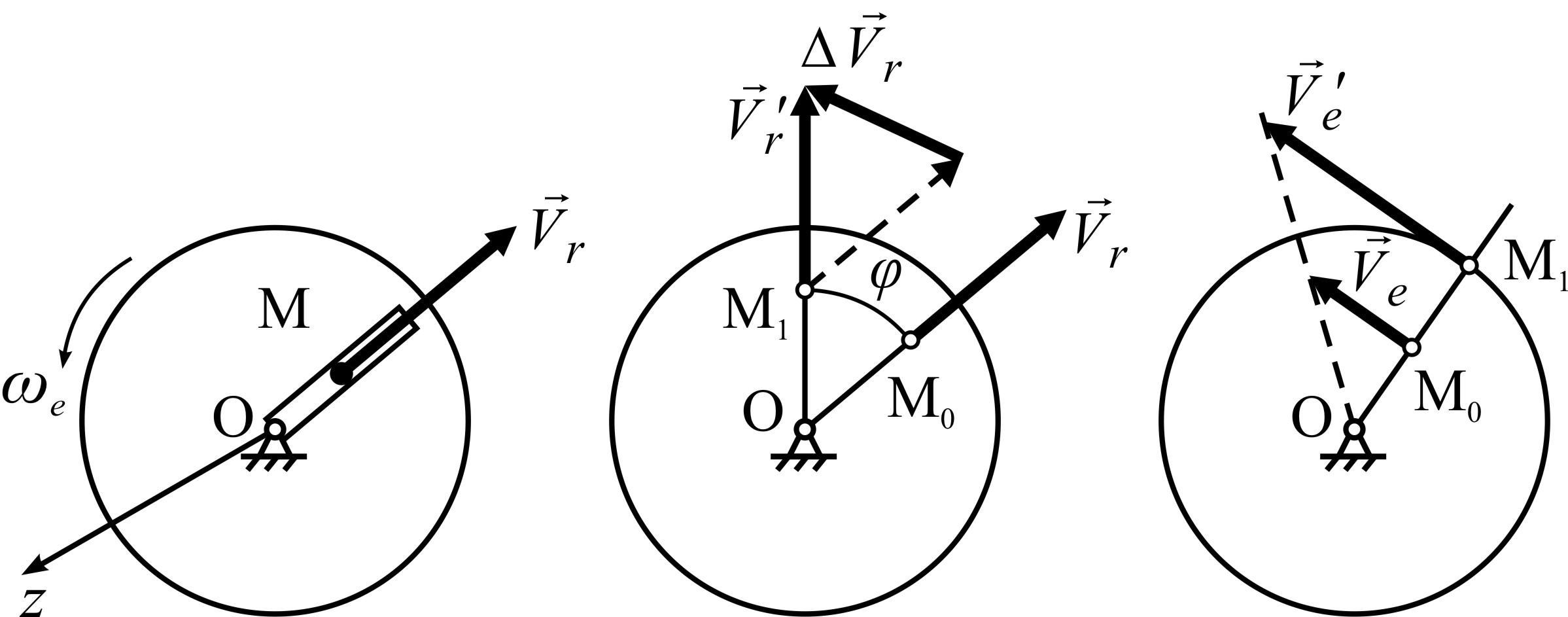
а) б) в)

Рисунок 4.7

Представим себе, что для изучения относительного и переносного движений имеется два разных секундомера.

1. Включим секундомер для изучения переносного движения. Выясним, как изменится относительная скорость при остановленном относительном секундомере за время . Тогда вектор в положении сохранит свой модуль, но приложен будет в точке, куда переместится точказа время(рис. 4.7,б). Модуль разности векторов и равен , где– угол поворота диска за время, т.е.

. (4.19)

Изменилась относительная скорость только за счет переносного движения (т. к. ).

2. Включим секундомер для изучения относительного движения. Выясним, как изменится переносная скорость , если точка переместилась из положения в положениена расстояние(рис. 4.7,в). Переносная скорость точки равна, переносная скорость точкиравна. Модуль разности векторови равен

. (4.20)

Изменилась переносная скорость только за счет относительного движения за время (т. к.).

3. На самом деле нет двух секундомеров для изучения относительного и переносного движений. Есть один секундомер и оба движения происходят одновременно. Выясним, какое ускорение получила точка М на самом деле.

Учитывая формулы (4.19) и (4.20), оно равно

. (4.21)

Если определить ускорение Кориолиса в данном примере по формуле (4.18), получим:

. (4.21')

Значит, полученное точкой в данном примере ускорение, есть ускорение Кориолиса.

Имеем физический смысл ускорения Кориолиса: ускорение Кориолиса измеряет изменение вектора относительной скорости в переносном движении и изменение вектора переносной скорости в относительном движении.

Ускорение Кориолиса еще называют поворотным; при переносном поступательном движении оно не возникает. Есть еще один случай сложного движения, при котором ускорение Кориолиса равно нулю: если векторы и параллельны, т. к. ,.

В качестве примера, иллюстрирующего определение ускорения Кориолиса, рассмотрим вопрос о том, почему правый берег реки Волга более крутой, чем левый?

Пример. Некоторая частица воды М движется со скоростью (рис. 4.8) по меридиану Земли с севера на юг. Определить величину и направление ускорения Кориолиса этой частицы, зная угловую скорость вращения Земли вокруг вертикальной оси.

Зная угловую скорость вращения Земли вокруг вертикальной оси

и географическую широту местоположения точки М, а также скорость , с которой движется частица по Земле, можно найти величину ускорения Кориолиса по формуле (4.18). Направлен вектор ускорения Кориолиса перпендикулярно медиональной плоскости по параллели с запада на восток.

В разделе «Динамика» будет доказано, что в относительном движении по поверхности Земли ускорению Кориолиса соответствует сила Кориолиса, направленная в сторону, противоположную этому ускорению. В нашем примере частицы воды будут прижиматься к правому берегу реки. Наблюдающееся в двухколесных железных дорогах преимущественное истирание правого рельса также объясняется действием Кориолисовой силы.

В этом заключается известный закон Бэра: Кориолисова сила вызывает дополнительное давление частиц воды к правому берегу в северном полушарии и к левому берегу в южном полушарии.