4.2 Способ наблюдения движений

Выясним, как наблюдать эти три движения. Представим себе плот, плывущий по реке со скоростью (рис. 4.2). ПассажирМ идет по плоту со скоростью , которая перпендикулярна скорости.

Рисунок 4.2

Имеем две системы координат:

– оси , связанные с плотом, наблюдатель I находится в точкеО;

– оси , связанные с берегом, наблюдатель II находится в точкеО₁.

Согласно данным выше определениям, давайте выясним, кто наблюдает движения: относительное, переносное, абсолютное?

Ответы:

1) Относительное движение наблюдает первый наблюдатель. Если события происходят ночью и пассажир М несет фонарь, то наблюдатель I увидит траекторию – прямую от одного берега к другому.

2) Что увидит второй наблюдатель? При постоянных скоростях ион увидит прямую, совпадающую с диагональю прямоугольника, построенного на векторахи. Это будетабсолютное движение.

3) Увидеть переносное движение не удастся ни одному из наблюдателей, т. к. надо представить себе, что в каждый миг мы остановим пассажира на плоту, т. е. наблюдаем за той точкой плота, с которой в данный момент совпадают подошвы пассажира.

Выводы:

1) Относительное движение точки наблюдают с подвижной системы отсчета.

2) Абсолютное движение точки наблюдают с неподвижной системы отсчета.

3) Переносное движение «наблюдают» с неподвижной системы отсчета, «остановив» относительное движение.

Прежде чем решить основную задачу установления зависимостей между кинематическими характеристиками движений, получим формулы, по которым они определяются.

4.3 Формулы для определения скоростей и ускорений точки

Относительная скорость точки равна первой производной от уравнения относительного движения, относительное ускорение точки равно второй производной по времени от уравнения относительного движения.

Берем производные по времени от формулы (4.1), помня о том, что координаты x, y, z – функции времени, а вектора .

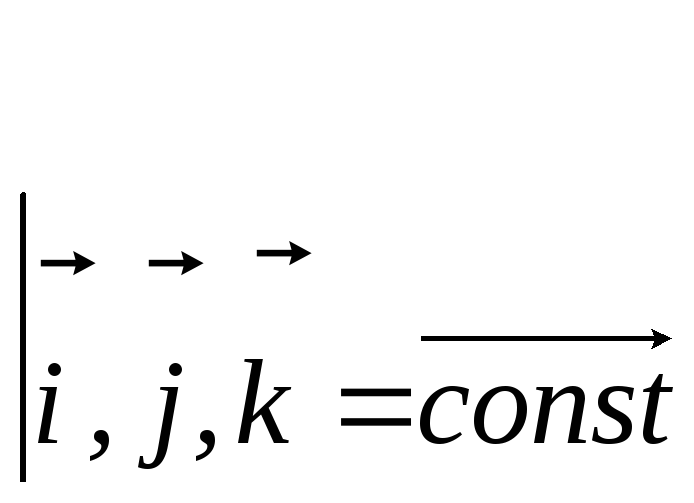, ; (4.4)

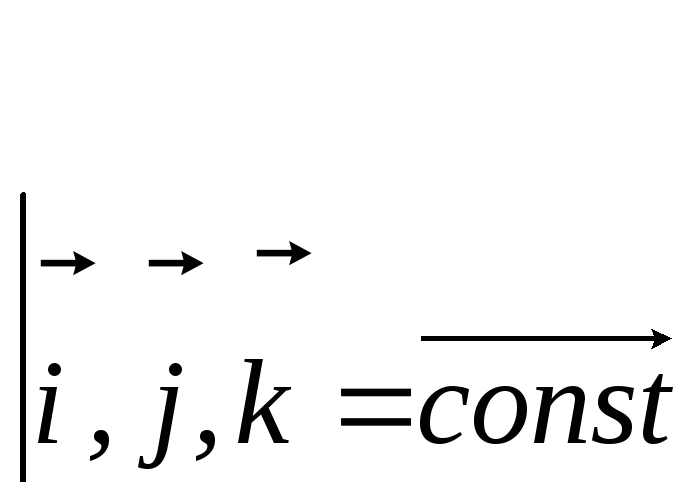, . (4.5)

Переносная скорость точки равна первой производной от уравнения переносного движения, переносное ускорение точки равно второй производной от уравнения переносного движения.

Берем производные по времени от формулы (4.2), помня о том, что теперь координаты x, y, z – фиксированы, а единичные вектора, оставаясь постоянными по модулю, при движении носителя меняют свои направления. Поэтому имеем:

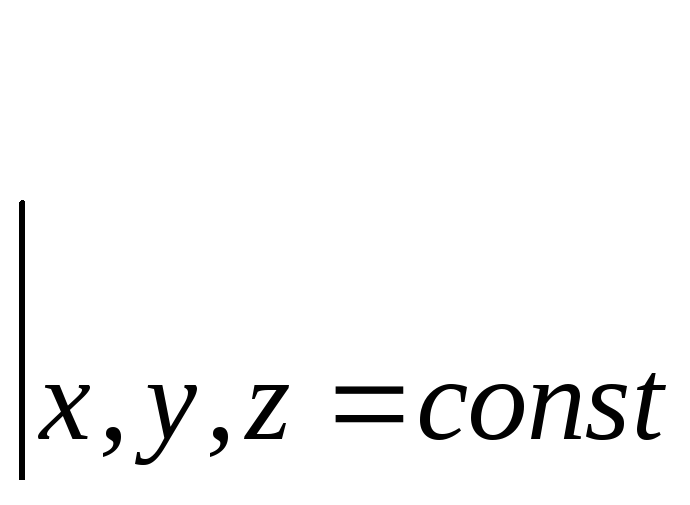, ; (4.6)

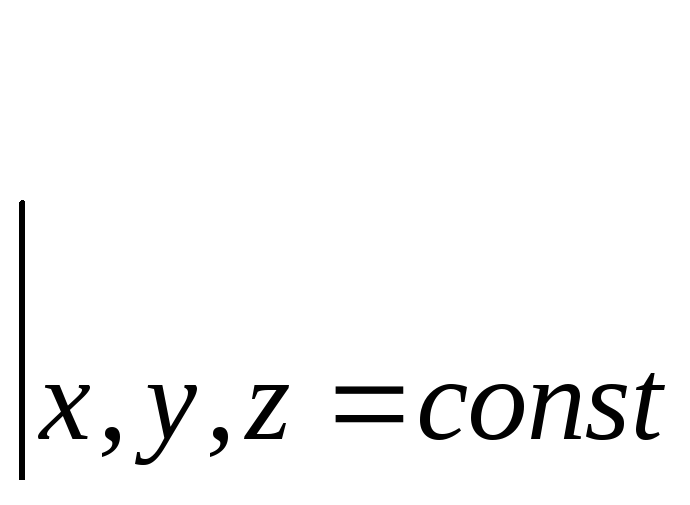, . (4.7)

Абсолютная скорость точки равна производной по времени от уравнения ее абсолютного движения.

Следовательно, берем производную от формулы (4.3), считая, естественно, что единичные вектора .

, . (4.8)

Абсолютное ускорение точки равно производной по времени от абсолютной скорости.

Следовательно, берем производную от формулы (4.8).

, . (4.9)

4.4 Теорема сложения скоростей

Вернемся к рисунку (4.1) и вспомним связь между радиусами-векторами ,и:, т.е.

. (4.10)

Возьмем производную по времени от векторного равенства (4.10) по правилам высшей математики, не накладывая никаких ограничений на координаты и единичные вектора . Помним только, что.

. (4.11)

Сравнив слагаемые, входящие в формулу (4.11) с формулами (4.4), (4.6), (4.8), получим

. (4.12)

Доказана теорема: абсолютная скорость точки, совершающей сложное движение, равна геометрической сумме переносной и относительной скоростей.