3.12 Методические указания к решению задач на тему «Плоское движение тела»

Задачи на эту тему можно подразделить на два основных типа, т.к. во многих практически важных задачах достаточно ограничиться определением скоростей и ускорений различных точек и всего тела в фиксированном положении плоского механизма.

Первый тип. Определение скоростей точек и мгновенных угловых скоростей звеньев, из которых состоит механизм.

Второй тип. Определение ускорений точек и мгновенных угловых ускорений звеньев, из которых состоит механизм.

Вэтих случаях наиболее распространенными и эффективными являютсяграфоаналитические методы определения скоростей (рис. 3.26).

Эти методы применяются для конкретного положения механизма, если известна (или легко определяется из условия задачи) скорость одной точки звена, а также известна прямая, на которой находится вектор скорости другой точки этого звена.

Рассмотрим первый метод. Как известно, связь между скоростями двух точек звена выражается основной теоремой (3.5): . Точка, скорость которой известна (например, точкаА), называется полюсом. Величина вращательной скорости точки В вокруг точки А определяется формулой . Векторвсегда направлен перпендикулярно отрезкуАВ.  – угловая скорость звена, которому принадлежат точки А и В.

Последовательность действий следующая:

1. Изучив, как движутся звенья механизма, определяем, какие звенья совершают плоское движение. На одном из звеньев выбираем полюс. Например, точка А – полюс. Необходимо найти скорости точек В и С этого звена и его угловую скорость.

2. Исходя из особенностей движения механизма, определяем линию, на которой лежит вектор искомой скорости – вектор скорости точки В. Из точки В проводим первую прямую, совпадающую с вектором .

3. Из точки В откладываем известный вектор скорости точки А – вектор .

4. Из конца вектора проводимвторую прямую, перпендикулярную отрезку АВ. На этой прямой будет расположен вектор вращательной скорости . Первую и вторую прямые проводим до их пересечения. В результате получаем треугольник скоростей, выражающий векторное равенство (3.5).

5. Решаем этот треугольник по известной стороне (длина известна) и трем углам. Решать этот треугольник можно тремя способами:

– с помощью теоремы синусов;

– проецируем стороны треугольника сперва на прямую, соединяющую точки А и В, а затем на прямую, перпендикулярную к отрезку АВ. В результате получим два скалярных уравнения с двумя неизвестными и, которые нужно решить.

– если треугольник скоростей построить в масштабе, то длины его сторон равны величинам скоростей (п. 3.6).

6. Значение мгновенной угловой скорости рассматриваемого звена определим по формуле 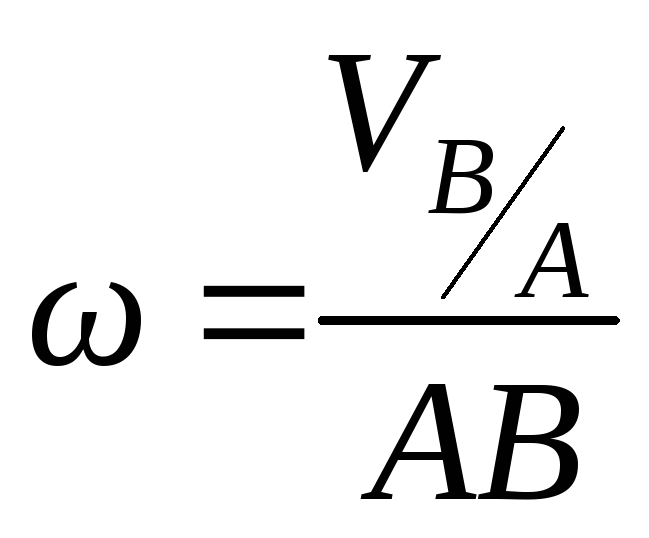и покажем дуговой стрелкой, направление которой зависит от направления вектора.

7. Затем можно найти аналогично скорость любой точки (например, точки С), для которой неизвестна линия расположения вектора . Используем ту же основную теорему , где– уже известная величина. Вектор изображаем перпендикулярно отрезкуСА по направлению дуговой стрелки .

Рассмотрим второй метод. С помощью мгновенного центра скоростей (м.ц.с.) определяются скорости точек звена, если уже определили положение м.ц.с., точки Р, одним из методов, изложенным в п. 3.8.

Далее последовательность действий такова:

1. На рассматриваемом звене надо найти точку, скорость которой либо известна, либо найдена из условия задачи. Например, скорость точки А, .

2. Соединив точку А и точку В, скорость которой нужно определить, с точкой Р, необходимо найти значения мгновенных радиусов вращения этих точек, т.е. расстояния АР и ВР.

3. Согласно формуле (3.11), выражающей закон распределения скоростей точек плоской фигуры (в нашем случае звена), определяем скорость точки В и мгновенное значение угловой скорости 

. (3.27)

У каждого звена многозвенного механизма, совершающего плоское движение, свой мгновенный центр скоростей!

Рассмотрим третий метод. Теорема Грасгофа о проекциях скоростей двух точек на соединяющую их прямую применяется тогда, когда известен вектор скорости одной точки, например, , а определить нужно скорость другой точки, например, точкиВ. При этом прямая, на которой расположен вектор , известна. Если и β – углы, которые образуют вектора ис осьюАВx, то согласно (3.8) имеем , или. Отсюда,.

Угловую скорость звена в этом случае можно найти по формуле (3.27) только после того, как построим м.ц.с. звена, точку Р, на пересечении перпендикуляров к скоростям и.

Рассмотрим графоаналитические методы определения ускорений (рис. 3.27).

Первый метод применяется для конкретного положения механизма, если известно (или легко определяется из условия задачи) ускорение одной точки, например, точки А (точку А назовем полюсом), и прямая, на которой расположен вектор другой точки, например, точки В. Согласно основной теореме для ускорений точек плоской фигуры имеем векторное равенство (3.15): .

Последовательность действий следующая:

1. Изучив, как движутся звенья механизма, определяем, какие звенья совершают плоское движение. На одном из звеньев выбираем полюс. Например, точка А – полюс. Необходимо найти ускорения точек В и С этого звена и его угловое ускорение.

2. Исходя из особенностей движения механизма, определяем линию, на которой лежит вектор искомого ускорения – вектор ускорения точки В. Из точки В проводим первую прямую, совпадающую с вектором .

3. Поскольку, решая задачу о скоростях, мы научились определять угловую скорость звена , находим нормальное ускорение при вращении радиуса ВА вокруг полюса А . Направлен этот вектор от точкиВ к точке А.

4. Из точки В откладываем известный вектор ускорения точки А, вектор .Из конца этого вектора откладываем вектор .

5. Из конца вектора проводимвторую прямую, перпендикулярную к вектору . На этой прямой будет расположен вектор вращательного ускорения. Первую и вторую прямые проводим до его их пересечения. В результате получаем многоугольник ускорений, выражающий векторное равенство (3.15).

6. Решаем этот многоугольник: две его стороны известны – и , а две неизвестны –и. Величиныиможно определить двумя способами: аналитическим и графическим.

Аналитический способ. Для этого нужно спроецировать векторное равенство (3.15) на две взаимно перпендикулярные оси координат. Одну ось Вх направим по прямой, которая перпендикулярна к вектору . Проекция равенства (3.15) на эту ось даст следующее уравнение: . В этом уравнении одна неизвестная величина – . Определяем ее.

Проецируя векторное равенство (3.15), а, значит, стороны многоугольника ускорений, на ось Ву, которая совпадает с вектором . Получим. В этом уравнении тоже одна неизвестная величина.Определяем ее.

Графический способ. Необходимо построить многоугольник ускорений по формуле (3.15), отложив известные ускорения ив масштабе, а неизвестныеипровести под известными углами. Тогда длины сторон многоугольника ускорений равны величинам ускорений (п. 3.11).

7. Значение мгновенного ускорения рассматриваемого звена определим по формуле и покажем дуговой стрелкой его направление в зависимости от направления вектора.

8. Теперь уже можно найти ускорения всех точек звена. Найдем, например, ускорение точки С, для которой неизвестна прямая расположения искомого вектора . Применим основную теорему, взяв за полюс точкуА.

. (3.28)

Величины и направления всех векторов, входящих в правую часть формулы (3.28), известны:

– . Этот вектор направлен от точкиС к точке А;

– . Этот вектор направлен перпендикулярноАС по дуговой стрелке углового ускорения ε.

Изображаем вектора ,ив точкеС, а затем, выбрав произвольные оси координат Сх и Су, проецируем векторное равенство (3.28) на эти оси. Проекции искомого вектора инайдены. Модуль ускорения определим по теореме Пифагора

. (3.29)

Направление вектора найдем по направляющим косинусам

. (3.30)

Если построить многоугольник ускорений, выражающий векторное равенство (3.28) в масштабе, получим искомый вектор .

Второй метод. Этим методом целесообразно воспользоваться, если известны:

– ускорение одной точки, например, точки А;

– значение мгновенной угловой скорости звена ;

– значение мгновенного углового ускорения звена ε.

Воспользуемся формулами (3.18) и (3.19), с помощью которых находим положение мгновенного центра ускорений (точки Q). Ускорения всех точек звена находятся из пропорции (3.21). Например, для точки С имеем

.

Вектор изображаем под угломμ (3.18) к мгновенному радиусу CQ в зависимости от направления углового ускорения ε (рис. 3.24).

Примечания.

1. Особенностью задач, в которых колесо совершает плоское движение, является следующий факт. При качении без скольжения колеса по неподвижной поверхности расстояние от центра колеса, точки С, до мгновенного центра скоростей, точки Р, в процессе движения остается неизменным. Поэтому угловое ускорение колеса можно искать по формуле

. (3.31)

2. При плоском движении мгновенный центр скоростей плоской фигуры никогда не совпадает с мгновенным центром ускорений. Если т. Q ≡ т. Р ≡ т. О, то эти точки неподвижные, а, значит, плоская фигура вращается вокруг неподвижной оси, проходящей через точку О.

Самостоятельно

Дано:

Условие 1 Кривошип ОА (рис. 3.28, звено 1) механизма, изображенного на рисунке, вращается с постоянной угловой скоростью ω1. В данный момент времени кривошип составляет с горизонтом угол α, а шатун АВ (звено 2) составляет с горизонтом угол β = 45°. Колесо 3 катится по горизонтали без скольжения. Заданы величины: α = 15о, ω1 = 2 с-1, АО = l1 = 0,2 м, АВ = l2 = 0,6 м.	Рисунок 3.28
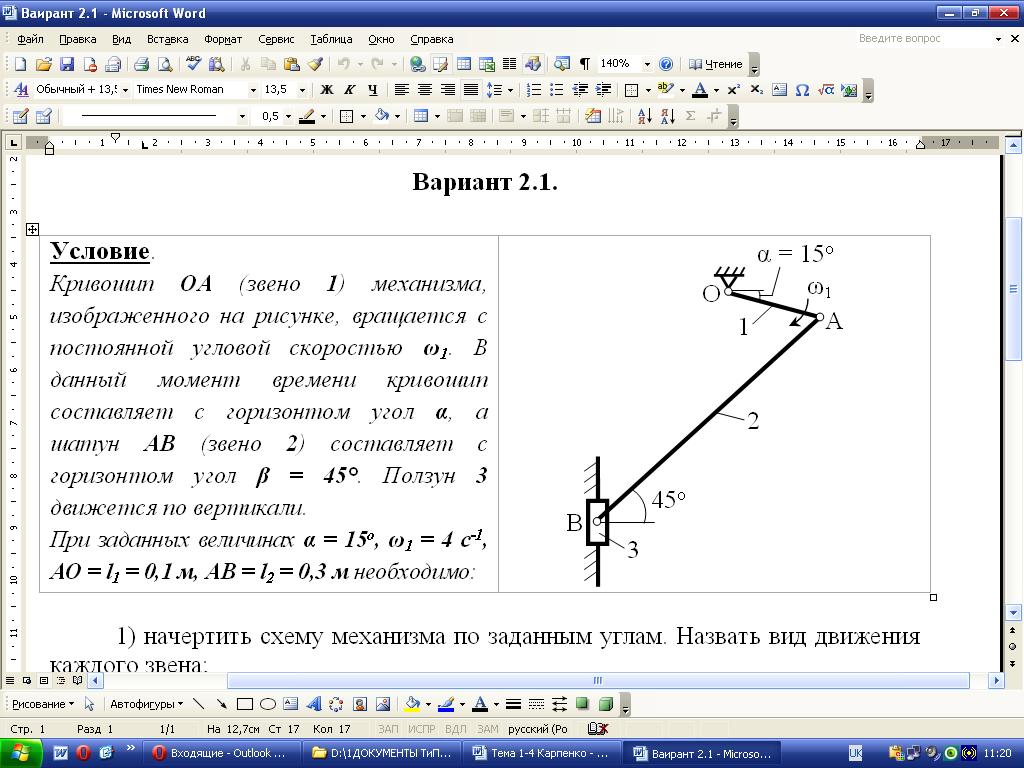
Условие 2 Кривошип ОА (рис. 3.29, звено 1) механизма, изображенного на рисунке, вращается с постоянной угловой скоростью ω1. В данный момент времени кривошип составляет с горизонтом угол α, а шатун АВ (звено 2) составляет с горизонтом угол β = 45°. Ползун 3 движется по вертикали. Заданы величины: α = 15о, ω1 = 4 с-1, АО = l1 = 0,1 м, АВ = l2 = 0,3 м.	Рисунок 3.29

Необходимо:

1) начертить схему механизма по заданным углам. Назвать вид движения каждого звена;

2) определить величину скорости и ускорения точки А. изобразить на рисунке вектор скорости и вектор ускорения.

3) определить величину и направление скорости точки В двумя способами:

– взяв за полюс точку А, записать векторную формулу скорости точки В; дать геометрическую интерпретацию этой формулы. Построить в масштабе план скоростей;

– определить положение мгновенного центра скоростей звена АВ (м.ц.с.) – точку Р. Записать формулу пропорциональности скоростей точек А и В (отношение расстояний до м.ц.с. получить с помощью теоремы синусов);

4) определить мгновенную угловую скорость звена АВ (ω₂) двумя способами:

– с помощью плана скоростей,

– с помощью м.ц.с.

Изобразить угловую скорость ω₂ на рисунке дуговой стрелкой.

5) определить величину и направление ускорения точки В двумя способами:

– взяв на полюс точку А, записать векторную формулу ускорения точки В. Построить эту формулу, найдя предварительно ускорение нормальное ;

– спроецировав векторную формулу для определения ускорения точки на оси Ву и Вх, найти и.

6) определить угловое ускорение звена АВ (ε₂); изобразить ε₂ на рисунке дуговой стрелкой.

Вопросы для самоконтроля

1. Какое движение твердого тела называется плоско-параллельным?

2. Записать кинематические уравнения движения плоской фигуры.

3. Назовите кинематические характеристики движения тела, совершающего плоское движение. Какая из них не зависит от выбора полюса?

4. Сформулируйте основную теорему для определения скорости любой точки плоской фигуры.

5. Сформулируйте основную теорему для определения ускорения любой точки плоской фигуры.

6. Что такое мгновенный центр скоростей? Приведите примеры нахождения положения м.ц.с.

7. Сформулируйте и запишите формулой закон распределения скоростей точек по отношению к м.ц.с.

8. Сформулируйте и запишите формулой закон распределения ускорений точек по отношению к м.ц.у.

9. Что называют планом скоростей? Какие необходимы данные для построения плана скоростей?

10. Что такое мгновенный центр ускорений? Как определить его положение?

11. Доказать, что векторы ипри плоском движении не зависят от выбора полюса.

12. Чему равны и как направлены вектора и?

13. Совпадают ли м.ц.с. и м.ц.у. в случае плоского движения тела?