4.7 Методические указания к решению задач на тему «Сложное движение точки»

При решении задач по данной теме применяется следующая последовательность действий:

1. Четкая формулировка составляющих сложного движения точки.

Остановив мысленно переносное движение, отвечаем на вопрос: что будет траекторией и каковы кинематические характеристики относительного движения точки.

Остановив мысленно относительное движение, т.е. закрепив точку на теле, связанном с подвижной системой координат, отвечаем на вопрос: каковы кинематические характеристики переносного движения точки.

2. В зависимости от вида траекторий составляющих движений применить формулы, полученные в темах 1, 2 и 3 для определения скоростей и ускорений точки.

3. Скорости точки при ее сложном движении связаны между собой теоремой сложения скоростей (4.12). Ускорения точки связаны между собой теоремами сложения ускорений:

– в случае криволинейной траектории переносного движения точки – формулой (4.15), в которой ускорение Кориолиса определяется формулами (4.17), (4.18);

– в случае переносного поступательного движения – формулой (4.16).

Найденные составляющие скоростей и ускорений точки изобразить на рисунке.

4. Указанные выше теоремы на практике можно реализовать двумя способами: аналитическим и графическим.

Аналитический метод (метод проекций). Для этого нужно выбрать Декартовы оси координат таким образом, чтобы были известны углы между осями координат и векторами, входящими в формулы (4.12), (4.15) или (4.16). Затем спроецировать векторные равенства, выраженные этими формулами, на оси координат и определить искомые величины.

Графический метод. Методом пользуются в случае, если точка движется на плоскости. Строят треугольник скоростей по формуле (4.12) и многоугольник скоростей по формулам (4.15) или (4.16) с последующим определением их сторон.

Рассмотрим применение теоремы сложения скоростей на примерах.

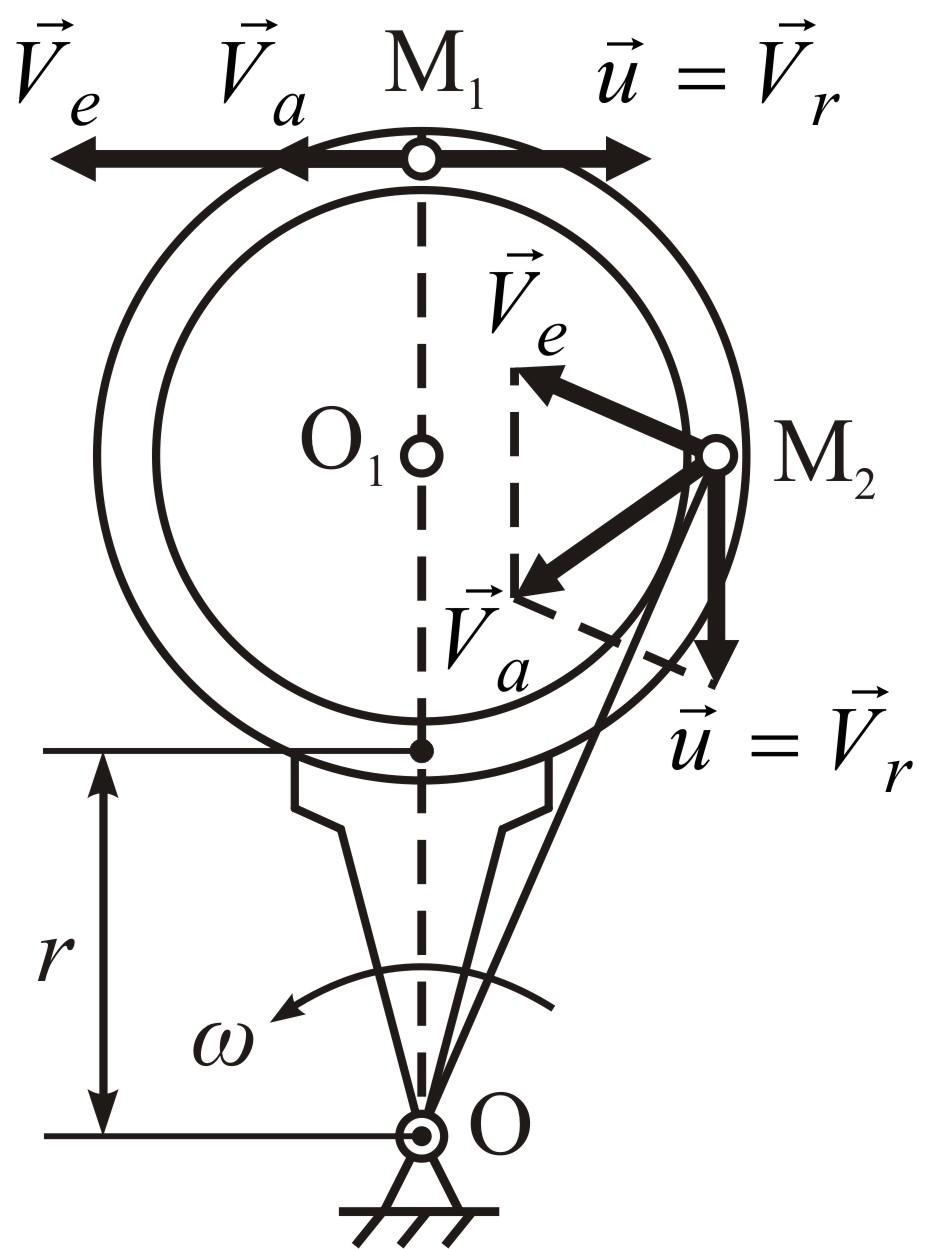
Пример 1. Полое кольцо радиуса жестко соединено с валом O так, что ось вала перпендикулярна к плоскости кольца (рис. 4.9). По кольцу движется шарик в направлении стрелки со скоростью . Вал вращается с угловой скоростью. Изобразить формулу сложения скоростей для точекМ1 и М2. Для решения любой задачи на тему «Сложное движение точки» надо определиться с тем, какое движение точки является относительным, переносным, абсолютным.

Рисунок 4.9

В данном примере относительное – движение шарика со скоростью по окружности с центром в точкеО₁ . Значит, для любого положения шарика. Переносное – движение шарика, скрепленного с кольцом, т.е. радиус окружности переносного движения в точкеМ₁  , в точкеМ₂ . Поэтому переносные скорости в точкахМ₁ и М₂ разные.

, направлена по , т. е. влево.

, направлена перпендикулярно к радиусу ОМ₂ по .

Вектор абсолютной скорости точки М₁ равен разности , если. Вектор абсолютной скорости точкиМ₂ равен геометрической сумме векторов и, т.е. направлен по диагонали параллелограмма, построенного на векторахи.

Пример 2. В кривошипно-кулисном механизме с поступательно движущейся кулисой ВС кривошип ОА вращается со скоростью (рис. 4.10). Концом А, соединенным шарнирно с поршнем, скользящим в прорези кулисы, он сообщает кулисе ВС возвратно-поступательное движение. Изобразить для ползуна А формулу сложения скоростей в заданном положении механизма.

Определимся с движениями точки А:

– относительное – движение точки А вдоль кулисы; по горизонтали направлена относительная скорость ;

– переносное – движение точки А вместе с кулисой по вертикали; переносная скорость направлена или вверх, или вниз по вертикали;

– абсолютное – движение точки А по окружности радиуса ОА; абсолютная скорость направлена по направлению угловой скорости перпендикулярноОА.

Изобразим абсолютную скорость , а векторы и подберем так, чтобы имела место формула .

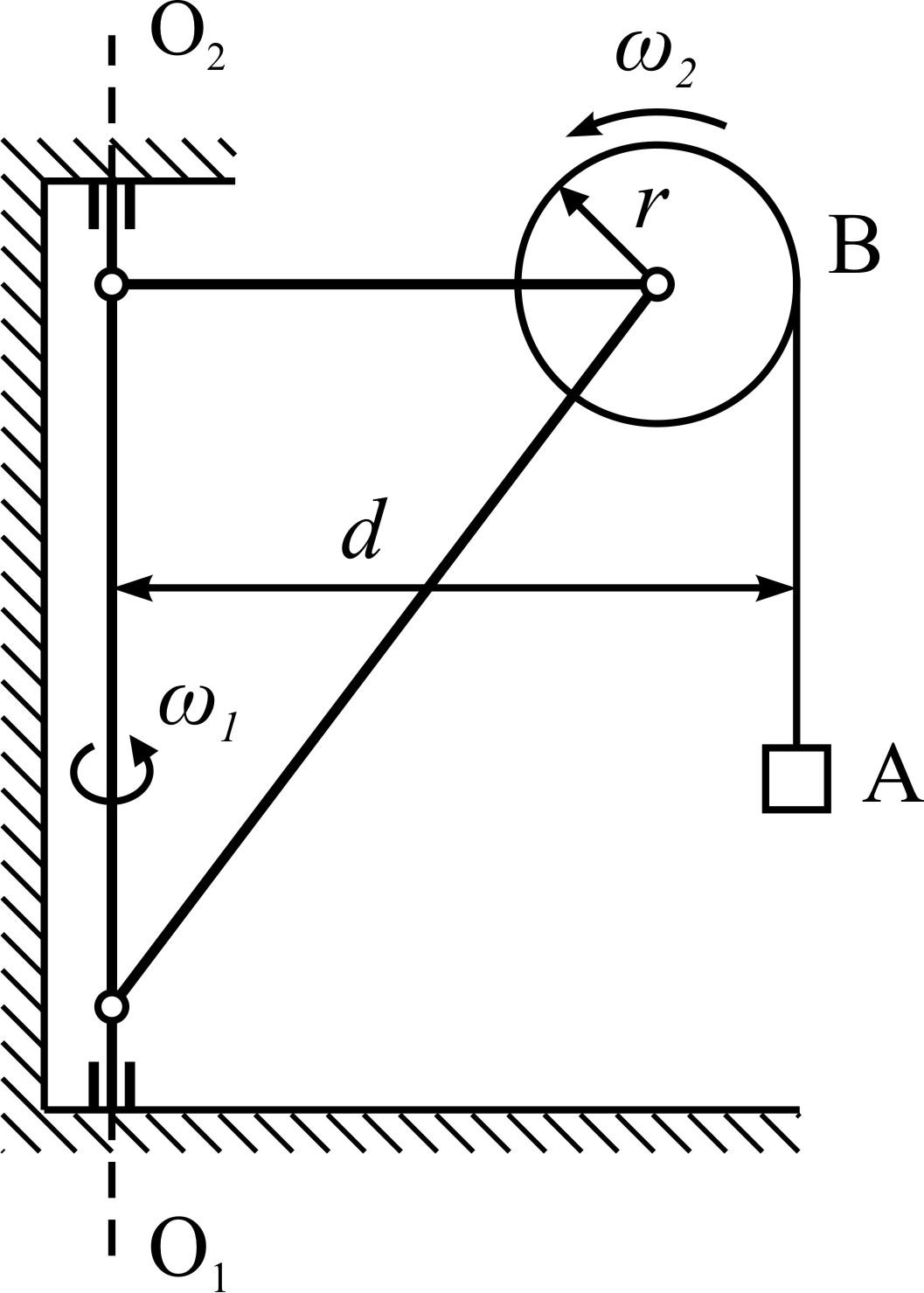
Пример 3. При вращении поворотного крана вокруг оси О1О2 с угловой скоростью грузА поднимается вверх посредством каната, навернутого на барабан В, который вращается с угловой скоростью (рис. 4.11). Изобразить формулу сложения скоростей. Определимся с движениями точки А (самостоятельно): – относительное – …?…, относительная скорость направлена …?…; – переносное – …?…, переносная скорость направлена …?…; – вектор абсолютной скорости направлен по диагонали прямоугольника со сторонами и (изобразить самостоятельно).

Рисунок 4.11

Пример 4. Ускорительный механизм строгального станка состоит из двух параллельных валов О и О₁ , кривошипа ОА и кулисы О₁В. Конец кривошипа ОА соединен шарнирно с ползуном, скользящим вдоль прорези в кулисе О₁В (рис. 4.12).

Изобразить формулу сложения скоростей для положения, изображенного на рисунке, при известной скорости вращения кривошипа .

Определимся с движениями точки А:

– относительное – …?…

– переносное – …?…

– вектор абсолютной скорости направлен перпендикулярно ОА по направлению .

Самостоятельно. Имея направление вектора , подобрать направления векторови.

Вопросы для самоконтроля

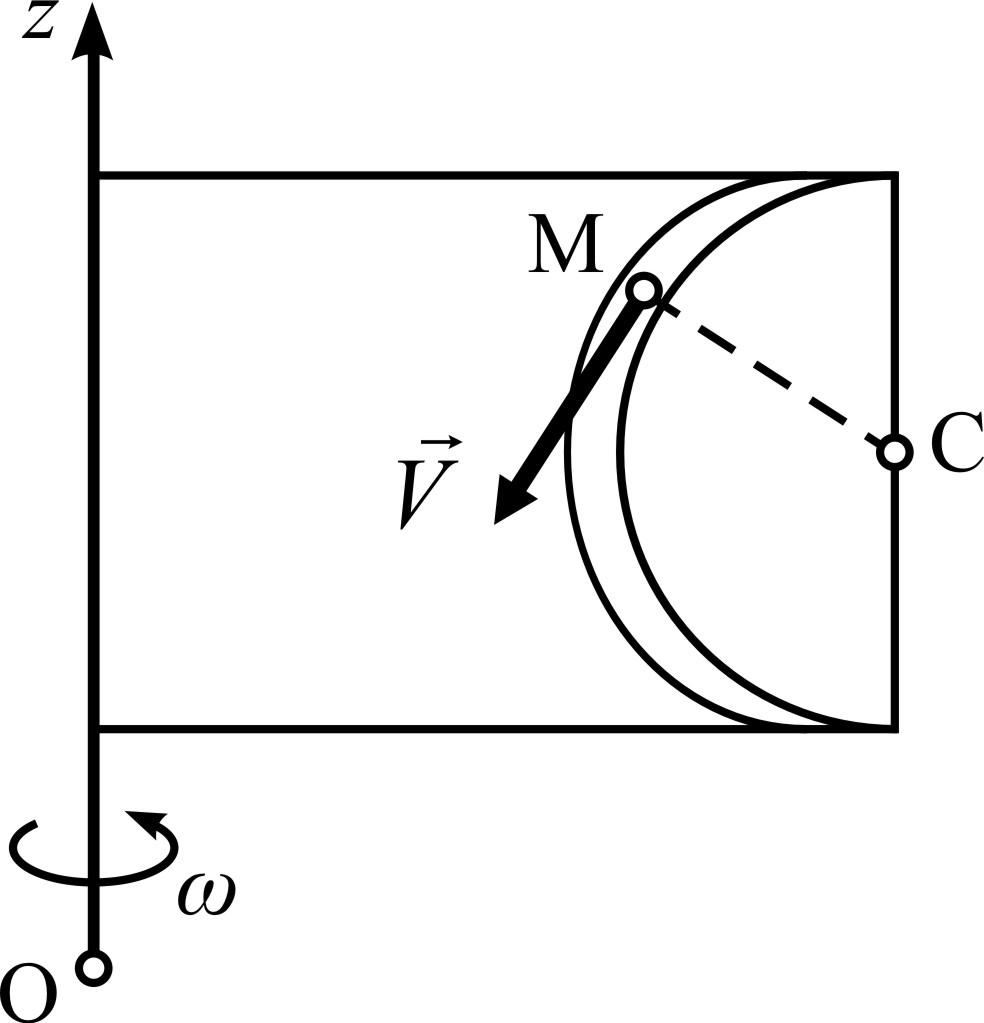
Рисунок 4.13

1. Сколько составляющих ускорений имеет точка М? Назовите эти составляющие. Пластинка вращается с постоянным угловым ускорением вокруг оси. По пластинке в прямолинейном канале с постоянной скоростьюдвижется точкаМ (рис. 4.13).

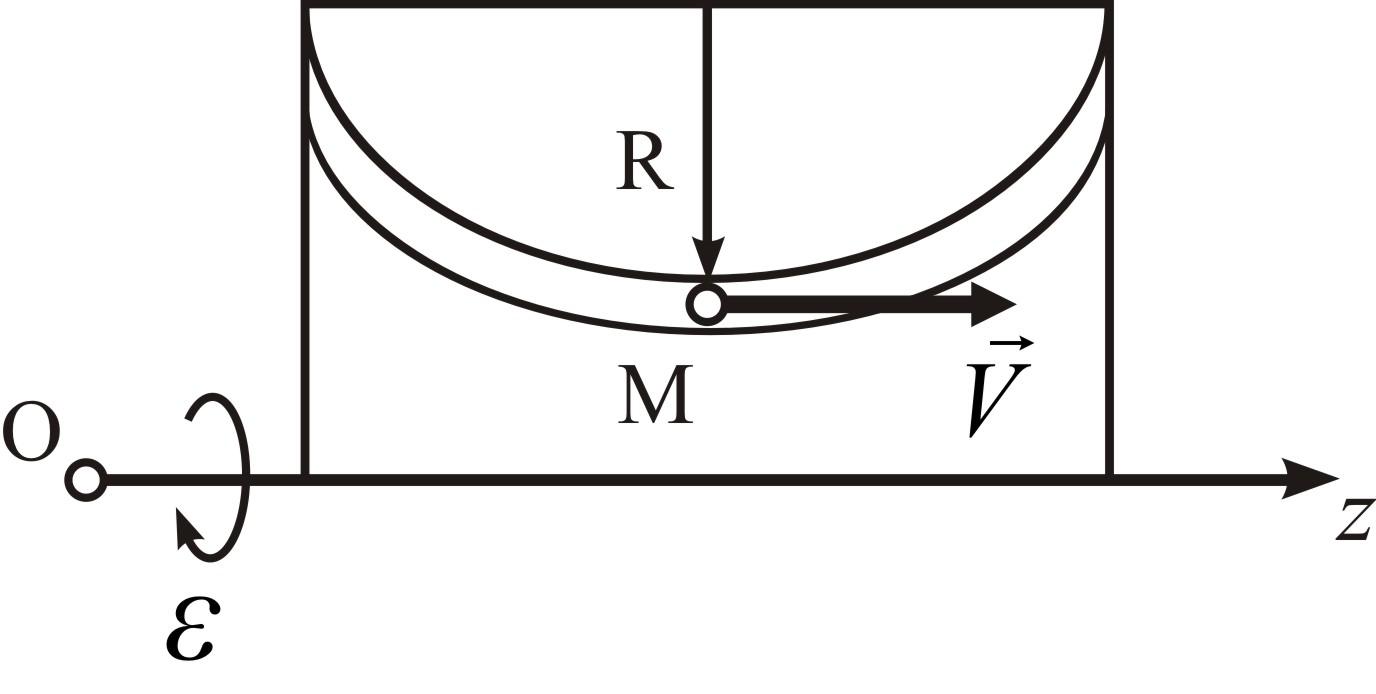
2. Сколько составляющих ускорений имеет точка М? Назовите эти составляющие. Пластинка вращается с постоянным угловым ускорением вокруг оси. По пластинке в прямолинейном канале с постоянной скоростьюдвижется точкаМ (рис. 4.14).				Рисунок 4.14
Рисунок 4.15	3. Сколько составляющих ускорений имеет точка М? Назовите эти составляющие. Пластинка вращается с постоянной угловой скоростью вокруг оси . По пластинке в криволинейном канале движется точка М с постоянной скоростью . Радиус кривизны канала R (рис. 4.15).
4. Сколько составляющих ускорений имеет точка М? Назовите эти составляющие. Пластинка вращается с постоянной угловой скоростью вокруг оси . По пластинке в криволинейном канале движется точкаМ с постоянной скоростью . Радиус кривизны канала R (рис. 4.16).			Рисунок 4.16
5. Сколько составляющих ускорений имеет точка М? Назовите эти составляющие. Пластинка вращается с постоянным угловым ускорением  вокруг оси . По пластинке в криволинейном канале движется точка с постоянной скоростью . Радиус кривизны канала R (рис. 4.17).		Рисунок 4.17

Рисунок 4.18

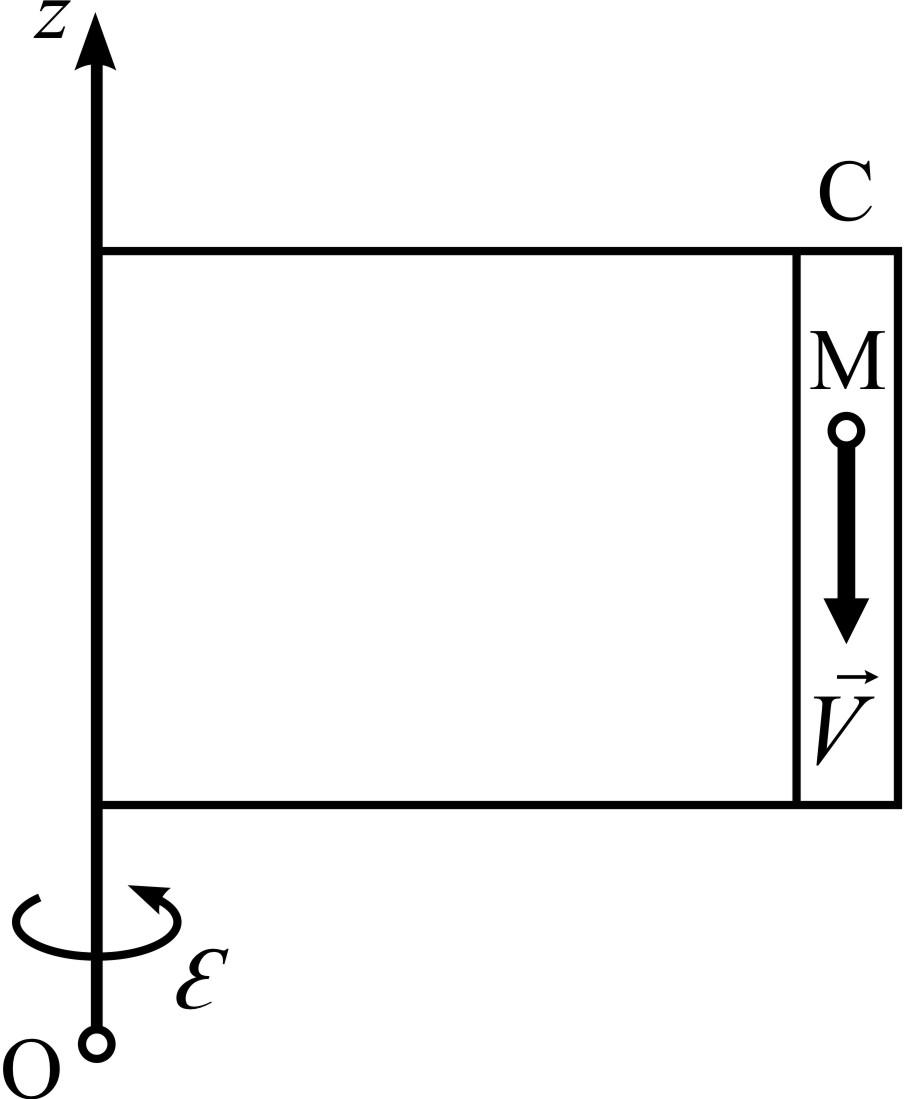
6. На тележке, движущейся по горизонтали вправо с ускорением , установлен электрический мотор, ротор которого вращается по закону(рис. 4.18). Сколько составляющих ускорений имеет точкаА, лежащая на ободе ротора? Назовите эти составляющие.

7. Какое движение точки называется относительным?

8. Какое движение точки называется переносным?

9. Какое движение точки называется абсолютным?

10. Сформулируйте теорему Кориолиса в случае переносного поступательного движения. Запишите формулу.

11. Сформулируйте теорему о сложении скоростей точки при сложном движении. Запишите формулу.

12. Запишите формулы, по которым определяется вектор и величина ускорения Кориолиса.

13. Сформулируйте теорему Кориолиса в случае переносного вращательного движения. Запишите формулу.

14. В некоторый момент времени точка имеет относительную скорость 3 м/с, переносную скорость 4 м/с. Определить абсолютную скорость точки в случаях, если угол между скоростями .

15. Как определяется направление ускорения Кориолиса (два способа)?