3.9 Определение ускорений точек плоской фигуры. Основная теорема

Имеем задачу: по данным уравнениям движения плоской фигуры S определить ускорения всех ее точек (рис. 3.20). Дано:

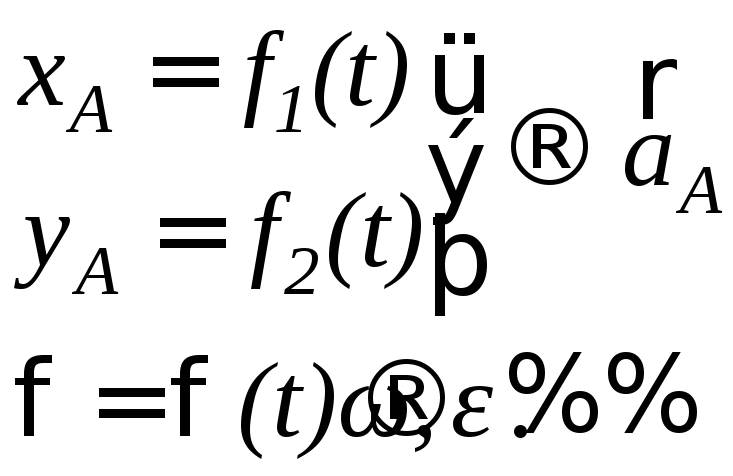
Определить: ускорение произ­вольной точки В.

В п. 3.3 мы определили ускорение точки А и угловую скорость и угловое ускорениеплоской фигурыS.

Для определения ускорения произвольной точки В плоской фи­гуры за полюс возьмем точку А. Найдем производную по времени от вектора скорости этой точки.

Имеем, согласно формуле (3.7), , и, следовательно,

. (3.12)

Рассмотрим слагаемые, входящие в формулу (3.12).

Первое слагаемое – ускорение полюсаА.

Второе слагаемое, обозначим его , –касательное или вращатель­ное ускорение точки В вокруг полюса А, равно .

Величина этого вектора равна

. (3.13)

Этот вектор перпендикулярный к вектору и направлен в ту же сто­рону, что и вектор вращательной скорости точкиВ вокруг полюса А, , или в противоположную сторону, сообразно тому, будет ли вращение фи­гуры ускоренным или замедленным. На рис. 3.20 векторнаправлен по направлению дуговой стрелки углового ускоренияε.

Третье слагаемое, которое обозначим , –нормальное или центрост­ремительное ускорение точки В вокруг полюса А

.

Определим двойное векторное произведение по формуле

.

Учитывая, что векторы ивзаимно перпендикулярны, имеем ска­лярное произведение, равно нулю. Следовательно,

.

Т.е. ускорение направлено от точки В к полюсу А и равно по величине

. (3.14)

Итак, вместо формулы (3.12), имеем:

(3.15)

. (3.16)

Таким образом, ускорение любой точки тела при плоском движе­нии равно геометрической сумме трех ускорений: – ускорения полюса (за полюс можно взять любую точку); – вращательного (касательного) ускорения точки во­круг полюса; – центростремительного (нормального) ускорения точки к полюсу.

На рис. 3.20 рассмотрен случай ускоренного вращения плоской фигуры. В случае за­медленного вращения покажем построение слагаемых ускорений на рис. 3.21.

Рисунок 3.21

Формулы (3.15) и (3.16) отражают основную теорему, по которой определяется ускорение любой точки плоской фигуры.

Замечая, что ускоре­ния ивзаимно перпен­дикулярны, получим:

. (3.17)

Угол µ, образуемый векто­ром и вектором, будет вычисляться по формуле

. (3.18)

3.10 Мгновенный центр ускорений. Определение ускорений точек с помощью мгновенного центра ускорений

Докажем, что в любой момент времени существуетточка плоской фигуры – назовем ее мгновенным центром ускорений, – ускорение кото­рой в этот момент времени равно нулю. Чтобы убедиться в существовании такой точки, проведем через произвольную точку А, ускорение которой известно , полупрямуюAL (рис. 3.22) под углом µ, который определяется по формуле (3.18). Откладываем угол µ в сторону, куда показывает дуговая стрелочка углового ускоре­ния фигуры ε.

Отложим на AL отрезок AQ, который равен:

. (3.19)

Определим ускорение точки Q согласно формуле (3.16):

,

где согласно формулам (3.17) и (3.19) .

При этом по построению вектор противоположен по направле­нию вектору, т.к. он составляет тот же уголµ (формула (3.18)) с векто­ром . Складывая вектораи, получим, что и требова­лось доказать.

Покажем, как построить мгно­венный центр ускорений, зная ускоре­ния двух точеки(рис. 3.23). В этом слу­чае отложим, кроме лучаAL (рис.3.22), луч ВМ под углом µ к вектору ускоре­ния в сторону, куда показывает дуговая стрелочкаε (рис. 3.23).

На пересечении лучей AL и ВМ будет находиться мгновенный центр ускорений (м.ц.у.) – точка Q.

Имея мгновенный центр ускоре­ний, точку Q, получаем весьма нагляд­ную картину распределения ускорений всех точек плоской фигуры. Действительно, применяя формулу (3.16) и замечая, что по определению ускорение точки Q равно нулю, взяв за полюс точку Q, получим ускорение некоторой точки С:

,

где вектор ускорения направим перпендикулярно к радиусуCQ (рис. 3.24), показав направление углового ускорения ε вокруг полюса Q; а вектор ускорения направим от точкиС к точке Q. Геометрическая сумма векторов ипо величине равна:

(3.20)

Ускорение любой точки плоской фигуры по величине пропорционально ее рас­стоянию до мгновенного центра ус­корений и направлено под углом µ (3.18) к радиусу–вектору, соединяющему рассматриваемую точку с мгновен­ным центром ускорений. Этот угол одинаков для всех точек плоской фигуры S.

Имеет место закон распределе­ния ускорений точек плоской фигуры: ускорения точек прямо пропорцио­нальны расстояниям от этих точек до мгновенного центра ускорений (фор­мула (3.21)):

(3.21)

Этот закон напоминает закон распределения ускорений точек тела, вращающегося вокруг оси, проходящей через точку Q и перпендикулярной к плоскости, в которой движется плоская фигура.