3.8 Способы определения положения мгновенного центра скоростей

1-й случай. Допустим, что заданы на­правления скоростей двух точек плоской фигуры и (рис. 3.13, он же 3.12). Вспомним, где находилась точкаР в п. 3.7 (рис. 3.11)? – на перпендикуляре, восста­новленном к вектору скорости . Точно также можно было доказать, что точкаР находится на перпендикуляре, восстанов­ленном к вектору скорости точки В. Отсюда вывод: в точке пересечения перпендикуляров к скоростям двух точек плоской фигуры находится мгновенный центр скоростей

Рисунок 3.13

2-й случай. Скорости двух точек плоской фигуры параллельны, точки лежат на общем перпендикуляре к скоростям этих точек (рис. 3.14,а; 3.14,б).

а)

б)

Рисунок 3.14

Т. к. имеет место формула (3.10), т. е. скорости точек прямо пропорциональны их расстояниям до м.ц.с., имеем следующее: точка Р находится на пересечении перпендикуляров к скоростям то­чек А и В с линией, соединяющей концы векторов и, изображенных в масштабе.

Иллюстрация таких случаев представлена на рис. 3.15. На рис. 3.15,а диск 3 находится между досками 1 и 2, которые движутся с известными скоростями и. На рис. 3.15,б диск 3 находится между двумя тросами, которые намотаны на колеса 1 и 2, вращающимися с разными угловыми скоростями ω₁ и ω₂.

Самостоятельно.Найти положение мгновенного центра скоростей диска 3.

3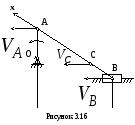-й случай. Скорости двух точек плоской фигуры параллельны, точки не лежат на одном перпендикуляре к скоростям этих точек. Проиллюстрируем это на кривошипно-шатунном механизме (рис. 3.16).

Восстановим перпендику­ляры к векторам и, они будут параллельны, т.е. не пере­секутся, а, значит,в данный мо­мент времени мгновенного цен­тра скоростей нет.

Применив теорему о про­екциях скоростей точекА и В на направление соединяющего их отрезка, на ось Вх (формула (3.8)), убе­димся в том, что , т.е. согласно формуле (3.5) скорость, а, значит,мгновенная угловая скорость звена АВ равна нулю. Такое движение называется мгновенно-поступательное в смысле распределения скоростей. (Скорость любой точки С звена АВ равна скоростям точек А и В; ускорения точек звена АВ при этом не будут одинаковы!).

4-й случай. Если колесо катится по непод­вижной поверхности без скольжения (рис. 3.17), то мгновенный центр скоростей находится в точке Р – точке касания колеса с неподвижной поверхностью.

Эта точка принадлежит одновременно и колесу, и неподвижной поверхности; поэтому ее скорость в данный момент времени равна нулю.

Самостоятельно:

1) Покажите направления скоростей точек В и D при известной ско­рости центра колеса (рис. 3.18).

2) При известной угловой скорости ω₁ кривошипа ОА найдите направ­ление угловой скорости звена 2 (с помощью мгновенного центра скоростей) (рис. 3.19).