
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Уравнение
вида
![]() ,
где
,
где![]() и
и![]() – некоторые действительные числа,
называетсялинейным однородным
дифференциальным уравнением второго
порядка с постоянными коэффициентами.
– некоторые действительные числа,
называетсялинейным однородным
дифференциальным уравнением второго
порядка с постоянными коэффициентами.
Частное
решение этого уравнения будем искать
в виде
![]() ,
где
,
где![]() – постоянное число, которое необходимо
определить. Дифференцируя
– постоянное число, которое необходимо
определить. Дифференцируя![]() ,
получаем
,
получаем![]() и
и![]() .
Подставим полученные выражения в
исходное уравнение:
.
Подставим полученные выражения в
исходное уравнение:
![]() .
.
Множитель
![]() отличен от нуля, поэтому можно разделить
на него обе части уравнения и получить
эквивалентное уравнение
отличен от нуля, поэтому можно разделить
на него обе части уравнения и получить
эквивалентное уравнение![]() ,
из которого можно определить значения
параметра
,
из которого можно определить значения
параметра![]() .
Уравнение
.
Уравнение![]() называется характеристическим уравнением
линейного дифференциального уравнения
второго порядка с постоянными
коэффициентами
называется характеристическим уравнением
линейного дифференциального уравнения
второго порядка с постоянными
коэффициентами![]() .
Для построения характеристического
уравнения достаточно в дифференциальном
уравнении производные
.
Для построения характеристического
уравнения достаточно в дифференциальном
уравнении производные![]() ,
,![]() и функцию
и функцию![]() заменить на соответствующие степени
параметра
заменить на соответствующие степени
параметра![]() ,
рассматривая при этом функцию
,
рассматривая при этом функцию![]() как производную нулевого порядка.
как производную нулевого порядка.
Теорема.
Если
![]() и
и![]() ‑ частные решения уравнения
‑ частные решения уравнения![]() ,
то
,
то![]() есть общее решение этого уравнения.
есть общее решение этого уравнения.
Для
определения частных решений
![]() и
и![]() следует предварительно решитьхарактеристическое уравнение:
следует предварительно решитьхарактеристическое уравнение:
![]() .
.
Корни
характеристического уравнения равны
![]() .
.
При решении данного квадратного уравнения возможны три случая:
1.![]() ,
тогда характеристическое уравнение
имеет два различных корня
,
тогда характеристическое уравнение
имеет два различных корня![]() и
и![]() .
При
.
При![]() эти функции являются линейно-независимыми.
Действительно, если допустить обратное,
то должно выполняться соотношение
эти функции являются линейно-независимыми.
Действительно, если допустить обратное,
то должно выполняться соотношение![]() ,
где хотя бы один из коэффициентов
,
где хотя бы один из коэффициентов![]() или
или![]() отличен от нуля. Следовательно, можно
получить тождество
отличен от нуля. Следовательно, можно
получить тождество![]() ,
что противоречит здравому смыслу,
поскольку левая часть равенства
изменяется с изменением
,
что противоречит здравому смыслу,
поскольку левая часть равенства
изменяется с изменением![]() ,
в то время как правая часть постоянна.
Таким образом, общее решение для этого
случая имеет вид
,
в то время как правая часть постоянна.
Таким образом, общее решение для этого
случая имеет вид![]() .
.
2.![]() ,
тогда характеристическое уравнение
имеет единственный кратный корень
,
тогда характеристическое уравнение
имеет единственный кратный корень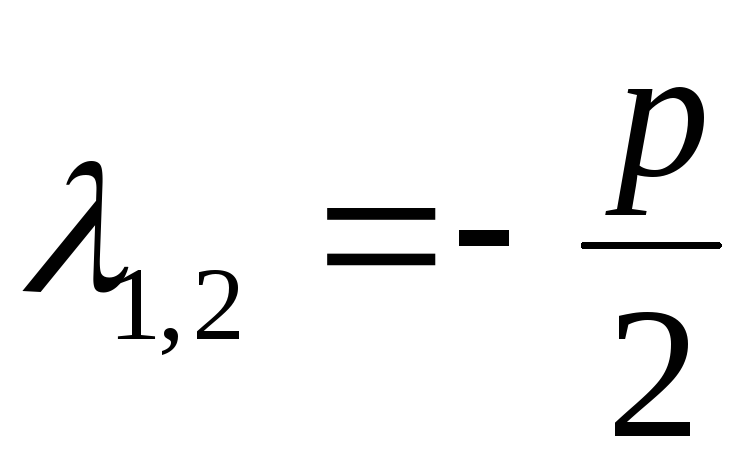 .
Поэтому частное решение дифференциального
уравнения будет иметь вид
.
Поэтому частное решение дифференциального
уравнения будет иметь вид![]() .
Всякое другое частное решение
.
Всякое другое частное решение![]() линейно независимое с
линейно независимое с![]() будет иметь вид
будет иметь вид![]() ,
где
,
где![]() – некоторая функция от
– некоторая функция от![]() ,
не являющаяся тождественно постоянной.
В результате дифференцирования
,
не являющаяся тождественно постоянной.
В результате дифференцирования![]() получаем:
получаем:

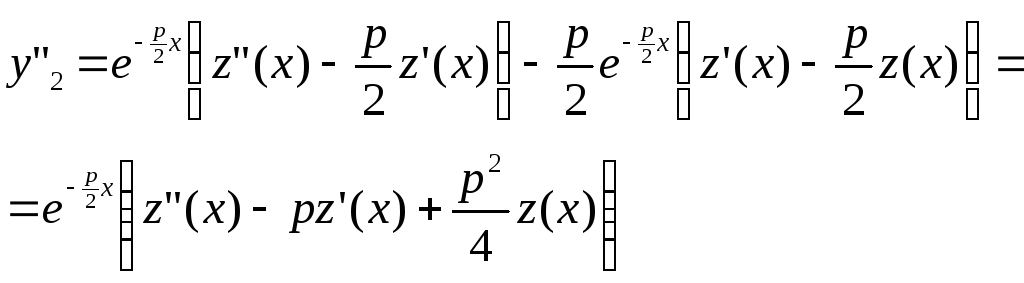
Подставляя
![]() ,
,![]() и
и![]() в исходное уравнение
в исходное уравнение![]() после сокращения на общий множитель
после сокращения на общий множитель![]() ,
получим
,
получим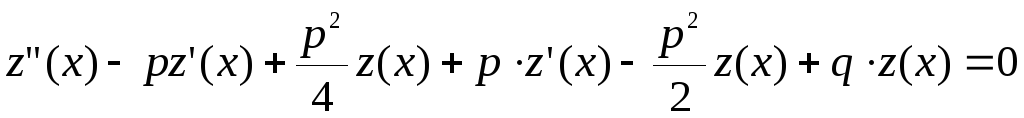 или
или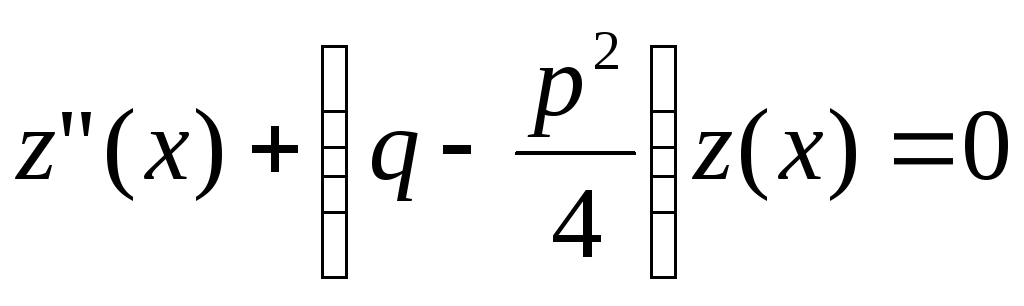 .
Поскольку, по условию
.
Поскольку, по условию![]() ,
получаем
,
получаем![]() .
Отсюда
.
Отсюда![]() и
и![]() ,
где
,
где![]() и
и![]() – произвольные постоянные. Следовательно,
– произвольные постоянные. Следовательно,![]() .
Поскольку,
.
Поскольку,![]() является частным решением и постоянные
является частным решением и постоянные![]() и
и![]() являются произвольными, можно принять
являются произвольными, можно принять![]() и
и![]() ,
при этом
,
при этом![]() .
.
Таким
образом, общее решение уравнения
![]() имеет вид:
имеет вид:![]() .
.
3.![]() ,
тогда характеристическое уравнение
имеет комплексно-сопряженные корни
,
тогда характеристическое уравнение
имеет комплексно-сопряженные корни![]() .
В этом случае частные решения
дифференциального уравнения будут
иметь вид
.
В этом случае частные решения
дифференциального уравнения будут
иметь вид![]() и
и![]() ,
а общее –
,
а общее –![]() .
.
|
Корни характеристического уравнения |
Частные решения |
Общее решение |
|
Действительные
|
|
|
|
Действительные
|
|
|
|
Комплексно-сопряженные
|
|
|
Пример.Найти общее решение дифференциального
уравнения
![]() .
.
Составим
характеристическое уравнение:
![]() .
Корни этого уравнения различные и
действительные
.
Корни этого уравнения различные и
действительные![]() и
и![]() ,
поэтому
,
поэтому![]() ‑ частные решения этого уравнения,
тогда
‑ частные решения этого уравнения,
тогда![]() ‑ общее решение данного уравнения.
‑ общее решение данного уравнения.
Пример.Найти частное решение дифференциального
уравнения
![]() ,
удовлетворяющее начальным условиям:
,
удовлетворяющее начальным условиям:![]() .
.
Корни
характеристического уравнения
![]() ‑ действительные и равные:
‑ действительные и равные:![]() ,
поэтому частные решения ‑
,
поэтому частные решения ‑![]() .
Тогда общее решение уравнения:
.
Тогда общее решение уравнения:![]() .
.
Для
определения частного решения в равенства
![]() и
и![]() подставим начальные условия.
подставим начальные условия.
Получим:
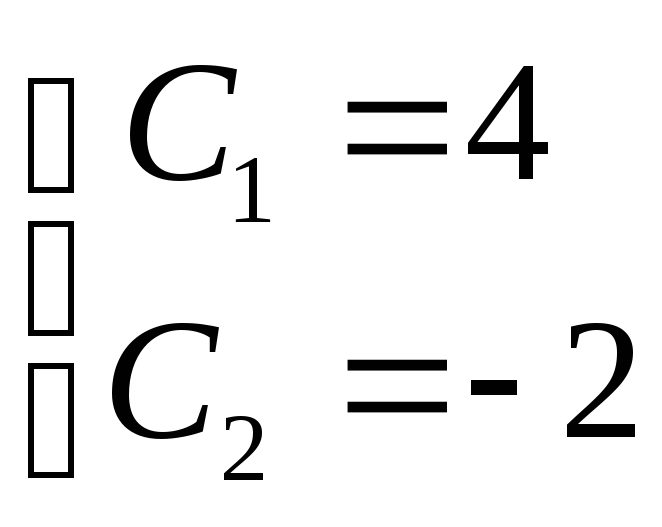 .
.
Подставив
эти значения в общее решение, найдем
частное
![]() .
.
Пример.Найти общее решение дифференциального
уравнения
![]() .
.
Корни
характеристического уравнения
![]() комплексно-сопряженные:
комплексно-сопряженные:![]() .
В этом случае
.
В этом случае![]() .
Общее решение будет:
.
Общее решение будет:![]() .
.
