Знакочередующиеся ряды

Ряд вида:

(6)

называют знакочередующимся.

• Признак Лейбница.Если последовательность стремится к нулю монотонно, то ряд (6) сходится.

Пример.Рассмотрим ряд . Для него , причем, , т.е. последовательность монотонно убывает и. Поэтому ряд сходится.

Для исследования монотонности последовательности удобно ввести некоторую вспомогательную (дифференцируемую) функциютакую, что, и исследовать функциюна монотонность, воспользовавшись критерием монотонности дифференцируемой функции.

Пример.Для ряда последовательностьпри.Для исследования монотонности последовательностирассмотрим вспомогательную функцию. Заметим, что. Поскольку. Дляфункцияубывает. Значит,, т.е.. Следовательно, последовательностьубывает и. По признаку Лейбница ряд сходится.

Абсолютная сходимость

Рассмотрим произвольный числовой ряд:

(7)

(никаких предположений о знаках членов не делаем). Ряд (7) называютабсолютно сходящимся, если сходится ряд

.

(8)

Пример.Ряд не является абсолютно сходящимся (хотя и сходится), так как ряд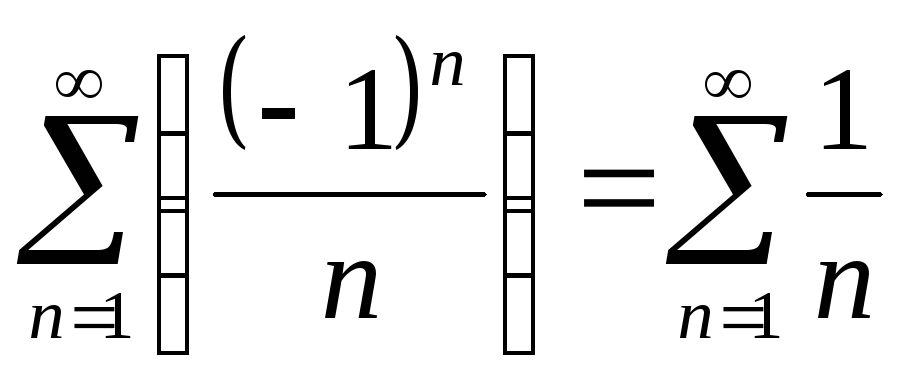расходится.

Пример.Ряд сходится абсолютно, т.к. рядсходится.

Теорема.Если ряд сходится абсолютно, то он сходится (в обычном смысле).

Это означает, что если сходится ряд (8), то сходится и ряд (7). Поскольку ряд ‑ положительный, то для его исследования можно использовать любой признак сходимости положительных рядов.

Функциональные ряды

В каждой точке определения функций если принять, тофункциональный ряд:

преобразуется в числовой ряд:

, который может оказаться как сходящимся, так и расходящимся.

Совокупность значений при которых функциональный ряд сходится, называетсяобластью сходимостиэтого ряда.

Суммой ряданазывается функция, определенная в каждой точке области сходимости ряда.

По определению предела означает, что_.

В общем случае зависит как от, так и от. Интерес представляют ряды, для которыхзависит только от.

Последовательность функций сходится равномернокна множестве, если.

Ряд сходится равномерно на множествеXк сумме, если последовательность его частичных суммсходится равномерно на множествек функции.

Теорема.Для того чтобы ряд 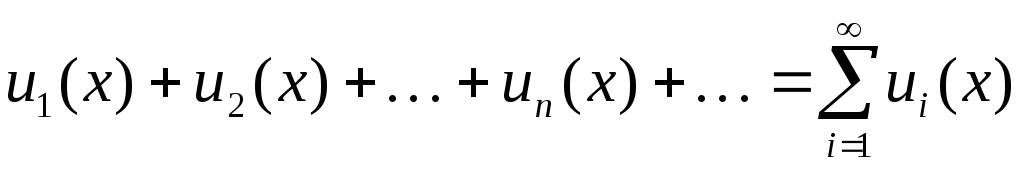сходился равномерно на множествеX, необходимо и достаточно, чтобы .

Для установления на практике равномерной сходимости рядов пользуются достаточными признаками.

• Признак равномерной сходимости, основанный на сравнении функционального ряда со сходящимся числовым.

Теорема. Если члены ряда удовлетворяют неравенствам, где, ачисла, не зависящие от, и, если рядсходится, то рядсходится равномерно на множествеX.

• Достаточные условия непрерывности суммы ряда.

Теорема. Если функции определены и непрерывны на множествеX и ряд сходится равномерно к суммеS(x) , то эта сумма будет непрерывна на множествеX.

• Свойства равномерно сходящихся рядов.

Теорема. Если функции определены и непрерывны на отрезкеи рядсходится равномерно нак сумме, то его можно почленно интегрировать на этом отрезке

.

Теорема. Если функции определены на отрезкеи существуют непрерывные производныена интервале, а рядсходится наи равномерно сходится ряд, то суммарядаимеет на интерваленепрерывную производную, причем,.

Таким образом, ряд можно почленно дифференцировать.