
- •Академия управления при Президенте Республики Беларусь
- •Содержание
- •Тема 4. Функции 9
- •Тема 5. Дифференциальное исчисление функций одной переменной 34
- •Тема 6. Исследование функций 45
- •Тема 7. Пространство 66
- •Тема 8. Неопределенные интегралы 100
- •Тема 9. Определенные интегралы 114
- •Тема 10. Понятие кратного интеграла 132
- •Тема 11. Ряды 140
- •Тема 12. Дифференциальные уравнения 171
- •Тема 4. Функции Лекция 15. Функции
- •Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
- •Контрольные вопросы к теме №4
- •Тема 5. Дифференциальное исчисление функций одной переменной Лекция 16. Дифференциальное исчисление функций одной переменной
- •Определение и смысл производной
- •Построение касательной к графику функции
- •Экономический смысл производной
- •Эластичность функции
- •Дифференцируемость функции
- •Правила дифференцирования
- •Производная сложной функции
- •Производная обратной функции
- •Дифференциал
- •Приближенные вычисления
- •Свойства дифференцируемых функций
- •Правила Лопиталя
- •Монотонность функции
- •Локальный экстремум
- •Исследование стационарных точек
- •Глобальный экстремум
- •Выпуклость и перегибы графика функции
- •Исследование функции и построение графика
- •Интерполяция и аппроксимация функций
- •Интерполяционный полином Лагранжа
- •Формула Тейлора
- •Основные разложения
- •Понятие об эмпирических формулах
- •Контрольные вопросы к теме №6
- •Тема 7. Пространство Лекция 18. Пространство
- •Точки, расстояние. Множества в
- •Последовательности в. Сходимость
- •Функции в. Предел. Теорема Гейне
- •Непрерывность функции в
- •Непрерывность на множестве
- •Теоремы о непрерывности
- •Дифференцируемость функций в. Частные производные
- •Дифференциал функции нескольких переменных
- •Необходимые условия дифференцируемости. Достаточные условия
- •Дифференцирование функции, заданной неявно и композиции функций
- •Полные дифференциалы и частные производные высших порядков. Признак полного дифференциала
- •Формула Тейлора
- •Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек
- •Условный экстремум функций нескольких переменных. Глобальный экстремум
- •Метод наименьших квадратов
- •Контрольные вопросы к теме №7
- •Свойства неопределенного интеграла
- •Замена переменных
- •Интегрирование по частям
- •Интегрирование рациональных функций. Метод рационализации
- •Вычисление
- •Вычисление
- •Вычисление
- •Вычисление
- •Контрольные вопросы к теме №8
- •Тема 9. Определенные интегралы Лекция 20. Определенные интегралы
- •Интегральные суммы
- •Необходимое и достаточное условие интегрируемости
- •Равномерно непрерывные функции
- •Интегрируемость непрерывных, разрывных и монотонных функций
- •Основные свойства определенного интеграла
- •Оценки интегралов. Формулы среднего значения
- •Основные правила интегрирования
- •Приложения определенного интеграла Площадь плоской фигуры
- •. Объемы тел вращения
- •Несобственные интегралы
- •Интегрирование неограниченных функций
- •Интегрирование по бесконечному промежутку
- •Приближенное вычисление определенных интегралов
- •Формула прямоугольников
- •Формула трапеций
- •Контрольные вопросы к теме №9
- •Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
- •Интегрирование функций многих переменных
- •Свойствакратного интеграла
- •Контрольные вопросы к теме №10
- •Тема 11. Ряды Лекция 22. Ряды
- •Основные понятия
- •Положительные ряды
- •Знакочередующиеся ряды
- •Абсолютная сходимость
- •Функциональные ряды
- •Степенной ряд
- •Ряды Фурье
- •Ряды Фурье четных и нечетных функций
- •Понятие о рядах Фурье непериодических функций
- •Контрольные вопросы к теме №11
- •Тема 12. Дифференциальные уравнения Лекция 23. Дифференциальные уравнения
- •Основные понятия
- •Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения семейства кривых
- •Геометрическое истолкование дифференциального уравнения
- •Задача Коши
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения
- •Метод Эйлера приближенного решения дифференциальных уравнений
- •Дифференциальные уравнения второго порядка
- •Задача Коши
- •Интегрируемые типы дифференциальных уравнений второго порядка
- •Случаи понижения порядка
- •Общие свойства решений линейных однородных дифференциальных уравнений второго порядка
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные уравнения второго порядка с постоянными коэффициентами
- •Линейные дифференциальные уравнения-го порядка
- •Контрольные вопросы к теме №12
- •Вопросы к экзамену
- •Литература
- •Высшая математика
- •220007, Г. Минск, ул. Московская, 17.
Формула прямоугольников
Вычисление
интеграла методом прямоугольников
заключается в определении суммы площадей
элементарных прямоугольников, на которые
делится площадь под кривой при делении
интервала интегрирования
![]() на
на![]() участков. При этом точность вычисления
будет тем больше, чем больше
участков. При этом точность вычисления
будет тем больше, чем больше![]() ,
однако при этом требуемое время вычисления
также увеличится.
,
однако при этом требуемое время вычисления
также увеличится.
Если за высоту прямоугольника принимается левая ордината участка, то метод вычисления называется методом левых прямоугольников, а если правая – методом правых прямоугольников.


Метод прямоугольников можно пояснить наглядно.
Формула вычисления интеграла методом левых прямоугольников имеют вид:
 ,
где
,
где

Аналогично
для правых прямоугольников:

Начальные
значения
![]() равны:
равны:
|
|
- для метода левых прямоугольников; |
|
- для метода правых прямоугольников. |
Формула трапеций
В
методе трапеций выполняется линейное
интерполирование функции
![]() .
На каждом интервале разбиения участок
кривой
.
На каждом интервале разбиения участок
кривой![]() заменяется хордой, стягивающей концевые
точки, а интеграл функции на участке
разбиения – площадью трапеции:
заменяется хордой, стягивающей концевые
точки, а интеграл функции на участке
разбиения – площадью трапеции: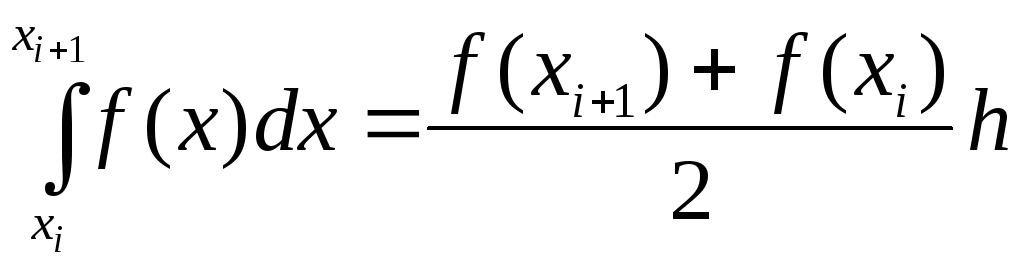 .
.
Тогда:

Контрольные вопросы к теме №9
Понятия интегральной суммы и определенного интеграла.
Верхняя и нижняя суммы Дарбу, их сходимость.
Понятие равномерной сходимости функции.
Приложения определенного интеграла.
Методы приближенного вычисления определенных интегралов.
Тема 10. Понятие кратного интеграла Лекция 21. Понятие кратного интеграла
Основные понятия:
двумерная интегральная сумма; двойной интеграл; повторное интегрирование; стандартная область интегрирования; кратный интеграл.
В
теории определенного интеграла для
нахождения площади криволинейной
трапеции вводится понятие интегральной
суммы, пределом которой является
определенный интеграл. Определенный
интеграл существует для трех типов
функций: непрерывных, кусочно-непрерывных
и монотонных. Задача интегрирования
может быть также сформулирована и для
функции
![]() переменных, заданной в ограниченной
области
переменных, заданной в ограниченной
области![]() с измеримым объемом
с измеримым объемом![]() .
В этом случае не удается ввести простого
понятия первообразной и неопределенного
интеграла. Кратный интеграл вводится
аналогично определенному интегралу
как суммирование бесконечного числа
бесконечно малых величин, т.е. через
понятие
.
В этом случае не удается ввести простого
понятия первообразной и неопределенного
интеграла. Кратный интеграл вводится
аналогично определенному интегралу
как суммирование бесконечного числа
бесконечно малых величин, т.е. через
понятие![]() мерной
интегральной суммы, пределом которой
является
мерной
интегральной суммы, пределом которой
является![]() мерный
интеграл.
мерный
интеграл.
Интегрирование функций многих переменных
Понятие двумерной интегральной суммы, пределом которой является двойной интеграл, можно ввести на основе задачи об объеме тела.
Задача:Найти объем тела, ограниченного сверху
непрерывной поверхностью
![]() ,
снизу – конечной замкнутой областью
,
снизу – конечной замкнутой областью![]() плоскости
плоскости![]() и с боков – прямой цилиндрической
поверхностью, построенной на границе
объекта
и с боков – прямой цилиндрической
поверхностью, построенной на границе
объекта![]() и имеющей образующие, перпендикулярные
плоскости
и имеющей образующие, перпендикулярные
плоскости![]() .
.
Для
этого разобьем основание
![]() на конечное число элементарных ячеек
на конечное число элементарных ячеек![]() и в каждой из этих ячеек выберем точку
и в каждой из этих ячеек выберем точку![]() .
Объем такого элемента равен
.
Объем такого элемента равен![]() .
Объем всей фигуры можно приближенно
найти как сумму
.
Объем всей фигуры можно приближенно
найти как сумму с любой степенью точности в зависимости
от числа ячеек
с любой степенью точности в зависимости
от числа ячеек![]() и, соответственно, их размера. Если
предположить, что число элементарных
ячеек
и, соответственно, их размера. Если
предположить, что число элементарных
ячеек![]() бесконечно возрастает, а их диаметр при
этом является величиной бесконечно
малой, то можно получить точное выражение
для объема всей фигуры:
бесконечно возрастает, а их диаметр при
этом является величиной бесконечно
малой, то можно получить точное выражение
для объема всей фигуры:

Таким
образом, двойной интеграл имеет простой
геометрический смысл, он выражает
объем криволинейного цилиндрического
бруса, ограниченного сверху непрерывной
поверхностью![]() ,
снизу – конечной замкнутой областью
,
снизу – конечной замкнутой областью![]() плоскости
плоскости![]() и с боков – прямой цилиндрической
поверхностью, построенной на границе
объекта
и с боков – прямой цилиндрической
поверхностью, построенной на границе
объекта![]() и имеющей образующие, перпендикулярные
плоскости
и имеющей образующие, перпендикулярные
плоскости![]() .
.
Двумерной
интегральной суммой от данной
функции
![]() ,
определенной на области
,
определенной на области![]() называется сумма парных произведений
площадей элементарных ячеек
называется сумма парных произведений
площадей элементарных ячеек![]() области
области![]() на значения функции
на значения функции![]() в точке
в точке![]() .
.
Двойным
интегралом от функции
![]() определенной на области
определенной на области![]() называется предел соответствующей
двумерной интегральной суммы при
неограниченном возрастании числа
называется предел соответствующей
двумерной интегральной суммы при
неограниченном возрастании числа![]() элементарных ячеек
элементарных ячеек![]() и стремлении к нулю их наибольшего
диаметра
и стремлении к нулю их наибольшего
диаметра![]() при условии, что этот предел существует
и не зависит от способа разбиения области
при условии, что этот предел существует
и не зависит от способа разбиения области![]() на элементарные ячейки
на элементарные ячейки![]() и выбора точек
и выбора точек![]() в них.
в них.
Теорема.
Если область
![]() с кусочно-непрерывной границей
с кусочно-непрерывной границей![]() ограничена и замкнута, а функция
ограничена и замкнута, а функция![]() непрерывна в области
непрерывна в области![]() ,
то двойной интеграл
,
то двойной интеграл т.е. предел соответствующей двумерной
интегральной суммы существует и не
зависит от способа разбиения области
т.е. предел соответствующей двумерной
интегральной суммы существует и не
зависит от способа разбиения области![]() на элементарные ячейки
на элементарные ячейки![]() и выбора точек
и выбора точек![]() в них.
в них.
Так
как значение двойного интеграла не
зависит от вида элементарных ячеек, то
в дальнейшем целесообразно пользоваться
наиболее удобным для декартовой системы
координат разбиением на прямоугольную
сетку, образованную пересечением двух
систем прямых, параллельных соответственно
координатным осям
![]() и
и![]() .
В этом случае элементарными ячейками
являются прямоугольники, со сторонами
.
В этом случае элементарными ячейками
являются прямоугольники, со сторонами![]() и
и![]() .
Таким образом, в обозначении интеграла
можно учесть что
.
Таким образом, в обозначении интеграла
можно учесть что![]() .
Тогда:
.
Тогда:
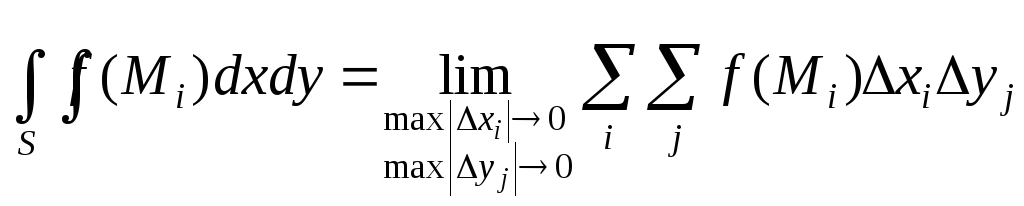 .
.
Для вычисления двойного интеграла применяется процедура повторного интегрирования.
Предположим
для определенности, что область
интегрирования
![]() представляет собой криволинейную
трапецию:
представляет собой криволинейную
трапецию:
![]() ,
,
![]() ,
,
где
![]() и
и![]() – однозначные непрерывные функции на
отрезке
– однозначные непрерывные функции на
отрезке![]() .
Важно отметить, что вертикаль, проходящая
через любую точку
.
Важно отметить, что вертикаль, проходящая
через любую точку![]() на отрезке
на отрезке![]() оси
оси![]() ,
пересекает границу области интегрирования
,
пересекает границу области интегрирования![]() только в двух точках: в точке входа
только в двух точках: в точке входа![]() и в точке выхода
и в точке выхода![]() .
Такая область называетсястандартнойотносительно оси
.
Такая область называетсястандартнойотносительно оси![]() .
.

Теорема.
Если для функции
![]() определенной в области
определенной в области![]() (стандартной относительно
оси
(стандартной относительно
оси
![]() ),
существует двойной интеграл
),
существует двойной интеграл
![]() и существует интеграл
и существует интеграл ,
то
,
то
При
этом, интеграл
 называетсяповторным. Таким образом,
вычисление двойного интеграла сводится
к вычислению двух интегралов: вначале
находится внутренний интеграл по
переменной
называетсяповторным. Таким образом,
вычисление двойного интеграла сводится
к вычислению двух интегралов: вначале
находится внутренний интеграл по
переменной![]() (при этом переменная
(при этом переменная![]() рассматривается как постоянная величина);
после этого полученное выражение
повторно интегрируется по переменной
рассматривается как постоянная величина);
после этого полученное выражение
повторно интегрируется по переменной![]() .
.
Задача
вычисления кратного интеграла может
быть обобщена на
![]() мерный
случай и аналогично решена путем сведения
кратного интеграла к повторному. Пусть
функция
мерный
случай и аналогично решена путем сведения
кратного интеграла к повторному. Пусть
функция![]() определена и ограничена в замкнутой
области
определена и ограничена в замкнутой
области![]() .
Область
.
Область![]() разбивается на
разбивается на![]() элементарных частей
элементарных частей![]() ,
таких что
,
таких что ,
пересечением любой пары элементарных
частей будет множество точек, размерность
которого не превышает
,
пересечением любой пары элементарных
частей будет множество точек, размерность
которого не превышает![]() .
.
В
каждой элементарной части выбирается
точка
![]() и составляется интегральная сумма:
и составляется интегральная сумма:
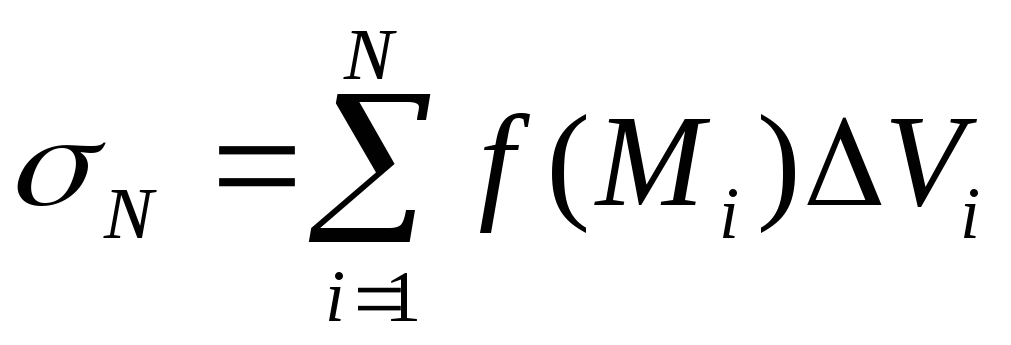 ,
,
 ,
,
где ![]() объемная
мера области
объемная
мера области![]() ;
;
![]() объемная
мера области
объемная
мера области![]() .
.
Для
того чтобы вычислить интегральную
сумму, необходимо, чтобы элементарные
части
![]() допускали исчисление объемной меры в
достаточно простой и редуктируемой
форме.
допускали исчисление объемной меры в
достаточно простой и редуктируемой
форме.
![]() кратным
интегралом функции
кратным
интегралом функции
![]() по области
по области![]() называется предел интегральной суммы
называется предел интегральной суммы![]() при
при![]() и, соответственно,
и, соответственно,![]() .
.![]() – наибольшая протяженность элементарной
области
– наибольшая протяженность элементарной
области![]() для данного разбиения.
для данного разбиения.
Этот
предел не должен зависеть от способов
разбиения
![]() на части и от выбора точек
на части и от выбора точек![]() в каждой из них. Указанный интеграл
можно представить в следующим образом:
в каждой из них. Указанный интеграл
можно представить в следующим образом:

По
форме этот интеграл сходен с определенным
интегралом
 ,
который также является пределом
интегральной суммы:
,
который также является пределом
интегральной суммы:
 ,
,
где
 ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Очевидно,
что в
![]() кратном
интеграле, как и в случае определенного
интеграла, интегральные суммы ограничены
снизу и сверху значениями сумм Дарбу
кратном
интеграле, как и в случае определенного
интеграла, интегральные суммы ограничены
снизу и сверху значениями сумм Дарбу![]() и
и![]() :
:
 ,
,
где
![]() ,
,![]() .
.
Свойствами
одномерных сумм Дарбу обладают и
![]() мерные
суммы. При этом для любой ограниченной
функции:
мерные
суммы. При этом для любой ограниченной
функции:
 и
и
 ,
,![]() .
.
Необходимым
и достаточным условием интегрируемости
функции является условие
![]() ,
что эквивалентно выражению:
,
что эквивалентно выражению:
 при
при
![]() .
.
Величина
![]() называетсяколебанием функции в
элементарной области
называетсяколебанием функции в
элементарной области![]() и является величиной положительной при
любом
и является величиной положительной при
любом![]() .
.
В
результате можно установить, что к числу
интегрируемых функций будут относиться
функции, непрерывные на замкнутой
области
![]() .
При вычислении
.
При вычислении![]() кратный
интеграл сводится к повторному интегралу,
т.е. вычислению обычного интеграла от
внутреннего интеграла кратности
кратный
интеграл сводится к повторному интегралу,
т.е. вычислению обычного интеграла от
внутреннего интеграла кратности![]() .
.

