Основные правила интегрирования

Теорема:Любая непрерывная на интервале функцияимеет на этом интервале первообразную. Одной из первообразных является функция:

,

где - любая фиксированная точка интервала_.

Так как две первообразные данной функции отличаются на постоянную, то согласно теореме, любая первообразнаянепрерывной на сегментефункцииимеет вид:

где - некоторая постоянная.

Полагая в последней формуле сначала , затем_, и используя первое свойства определенного интеграла, получим:

, .

Из этих равенств вытекает соотношение:

,

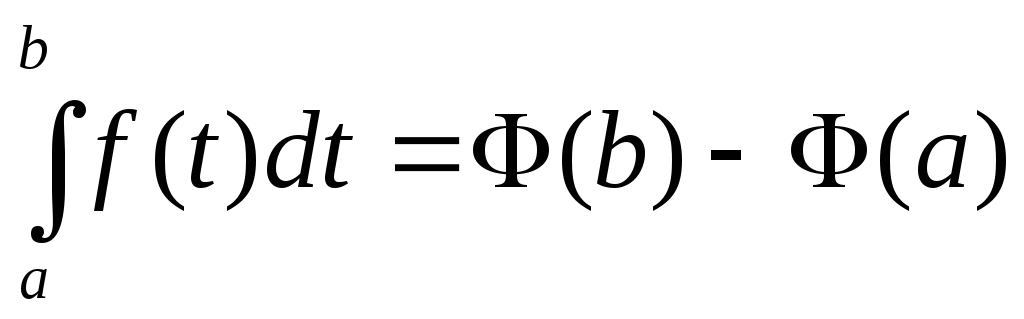которое называется основной формулой интегрального исчисления или формулой Ньютона – Лейбница.

Пусть выполнены следующие условия:

1) Функция непрерывна на отрезке;

2) отрезок является множеством значений некоторой функции, определенной на отрезкеи имеющей на этом отрезке непрерывную производную;

3) ,.

При этих условиях справедлива формула:

Указанная формула называется формулой замены переменной в определенном интеграле.

Пусть функции иимеют непрерывные производные на сегменте. Тогда имеет место следующая формула интегрирования по частям для определенных интегралов:

.

Так как и, то эту формулу можно записать следующим образом:

.

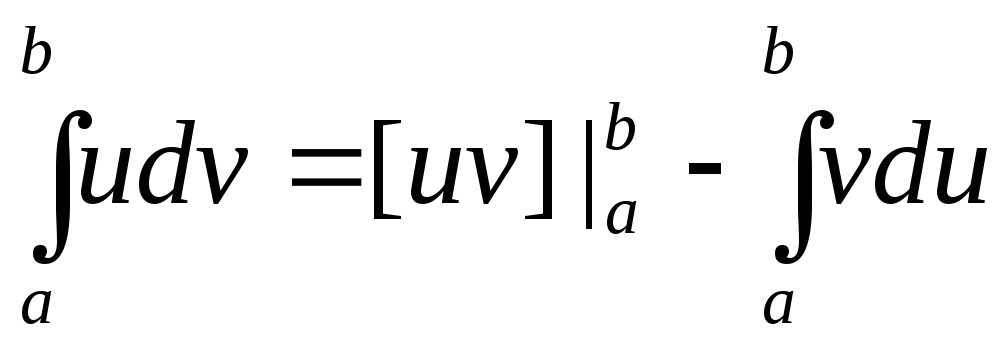Приложения определенного интеграла Площадь плоской фигуры

Определение: Плоская фигура – часть плоскости, ограниченная простой замкнутой кривой, при этом криваяназывается границей фигуры.

Определение: Мы будем говорить, что многоугольник вписан в фигуру , если каждая точка этого многоугольника принадлежит фигуреили ее границе.

Определение: Если все точки плоской фигуры и ее границы принадлежат некоторому многоугольнику, то мы будем говорить, что указанный многоугольник описан вокруг фигуры .

Замечание: Площадь любого вписанного в фигуру многоугольника не больше площади любого описанного вокруг фигурымногоугольника.

Пусть - числовое множество площадей вписанных в плоскую фигурумногоугольников, а- числовое множество площадей описанных вокруг плоской фигурымногоугольников. Очевидно, что множествоограничено сверху (площадью любого описанного вокруг фигурымногоугольника), а множествоограничено снизу (например, числом нуль).

Обозначим через точную верхнюю грань множества, черезточную нижнюю грань множества.

Числа иназываются соответственнонижнейплощадью иверхнейплощадью фигуры

Замечание: Нижняя площадь фигурыне больше верхней площади, т. е..

Определение. Плоская фигура называетсяквадрируемой, если верхняя площадь этой фигуры совпадает с ее нижней площадью. При этом число называетсяплощадью фигуры .

Теорема:Для того чтобы плоская фигура была квадирируемой, необходимо и достаточно, чтобы для любого положительного числаможно было указать такой описанный вокруг фигурымногоугольник и такой вписанный в фигурумногоугольник, что разностьплощадей которых была бы меньше,.

Определение:Криволинейной трапецией называется фигура, ограниченная графиком заданной на сегменте непрерывной и неотрицательной функции, ординатами, проведенными в точкахи, и отрезком осимежду точкамии.

Теорема: Криволинейная трапеция представляет собой квадрируемую фигуру, площадь которой может быть вычислена по формуле:

. Объемы тел вращения

Пусть - некоторое конечное тело. Рассмотрим всевозможные многогранники, вписанные в тело, и всевозможные многогранники, описанные вокруг тела.

Пусть - числовое множество объемов вписанных в тело, а- числовое множество объемов описанных вокругмногогранников. Множествоограничено сверху (объемом любого описанного многогранника), а множествоограничено снизу (например, числом нуль).

Обозначим через точную верхнюю грань множества, а черезточную нижнюю грань множества.

Числа иназываются соответственнонижним объемом и верхним объемомтела.

Замечание:Нижний объемтелане больше верхнего объемаэтого тела, т. е..

Определение:Тело называется кубируемым, если верхний объемэтот тела совпадает с нижним объемом. При этом числоназывается объемом тела.

Теорема: Для того чтобы тело было кубируемым, необходимо и достаточно, чтобы для любого положительного числаможно было указать такой описанный вокруг теламногогранник и такой вписанные в теломногогранник, разностьобъемов которых была бы меньше.

Теорема: Пусть функция непрерывна на сегменте. Тогда тело, образованное вращением вокруг осикриволинейной трапеции, ограниченной графиком функции, ординатами в точкахи, и отрезком осимежду точкамии, кубируемо и его объемможет быть найден по формуле:

.