Интерполяция и аппроксимация функций

При табличной форме задания функции часто возникает ситуация, когда аргумент функции задан с большей точностью, чем позволяет таблица. В этом случае приходится прибегнуть к интерполяции (или интерполированию) – приближенному нахождению неизвестных значений функций по известным ее значениям в заданных точках.

Наиболее простым является линейное интерполирование, при котором допускается, что приращение функции пропорционально приращению аргумента. Если заданное значение лежит между приведенными в таблице значениямии, которым соответствуют значения функциии, то считают, что:

.

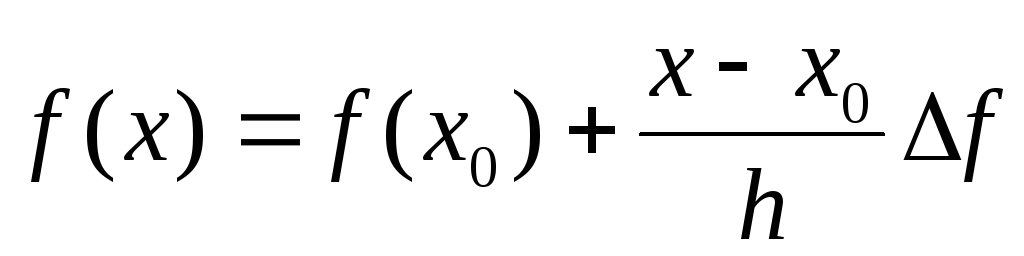Если по заданным значениям функции необходимо найти приближенное значение аргумента, то такая операция называется обратным интерполированием.

В общем виде интерполяционная задачасостоит в построении обобщенного многочлена, принимающего значения исследуемой функциина конечном множестве(область задания функции). Указанный многочлен должен удовлетворять условиям. Точкиназываютсяузлами интерполирования.

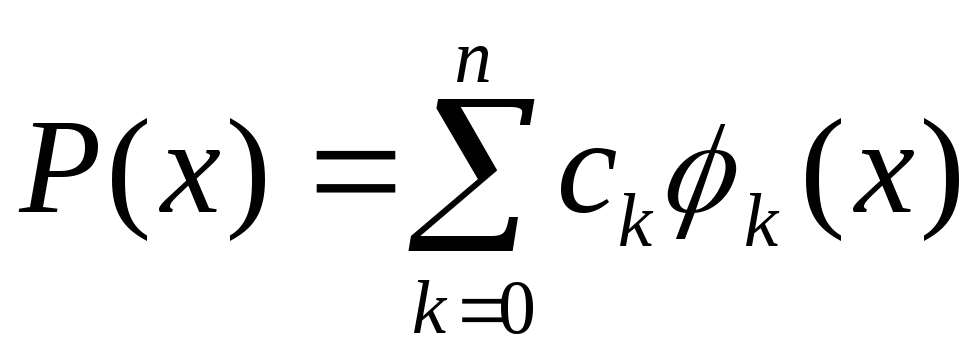В частности, если , а множество, искомый многочлен имеет линейную структуру и может быть представлен в виде, где – коэффициенты разложения, а– линейно независимые нафункции.

Условия интерполирования можно представить в виде системы уравнений:

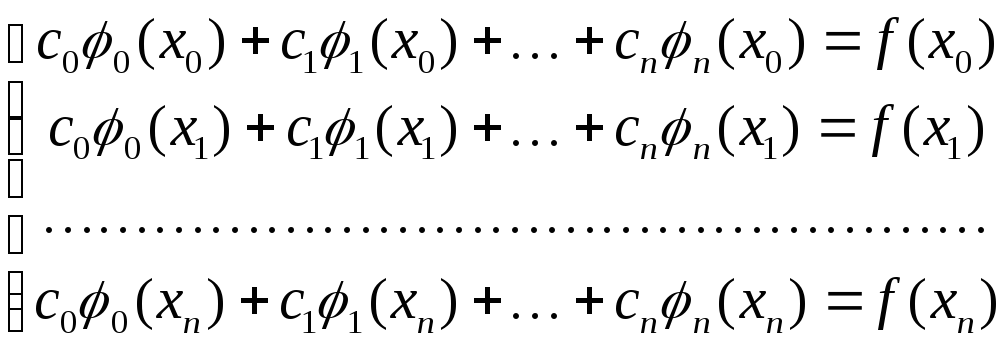
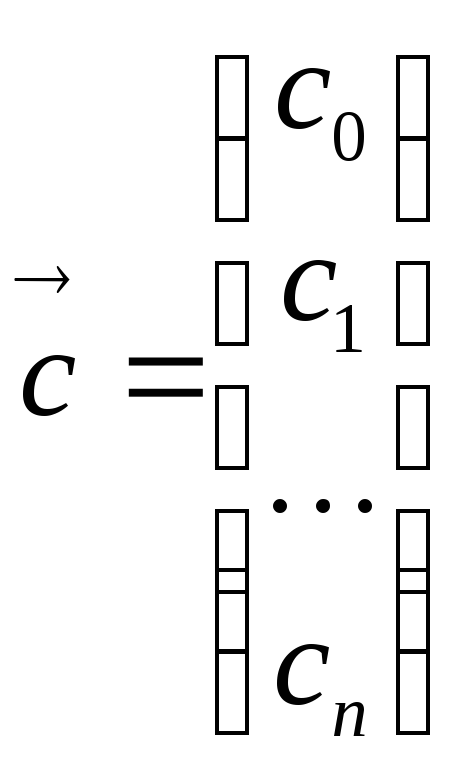
К системе можно применить векторно-матричную форму записи _, если ввести обозначения:

, ,

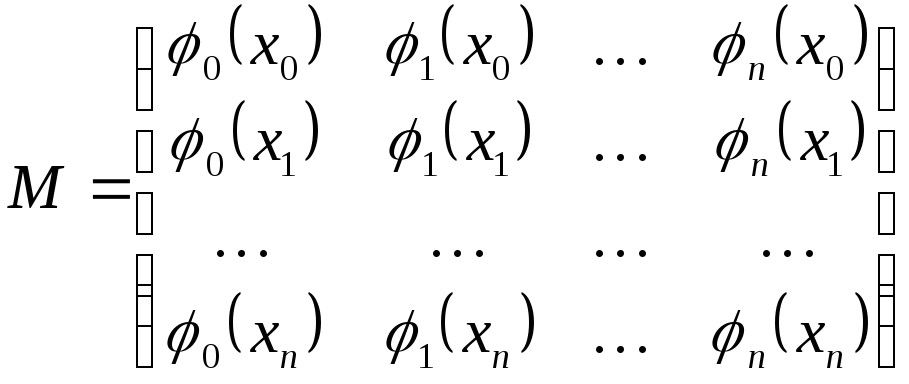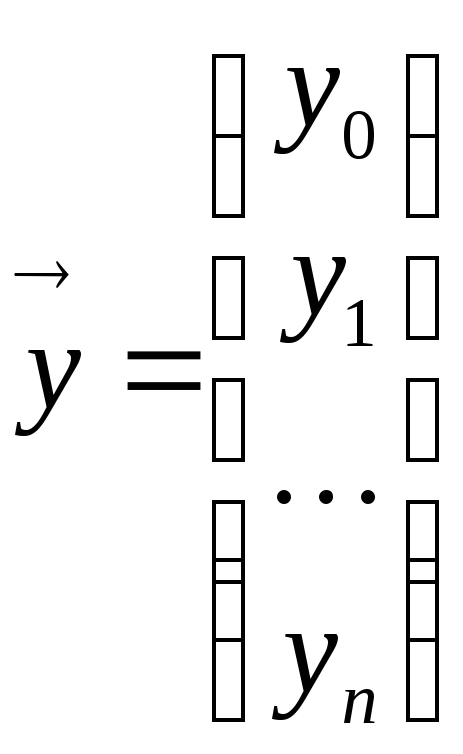
Если семейство функций составляет базис на, то условия интерполированияоднозначно удовлетворяются с помощью выбора коэффициентов. Если число узлов интерполирования не соответствует размерности базиса, то решение задачи интерполирования неоднозначно. Возникающую при этом неопределенность можно устранить путем введения дополнительных условий, налагаемых на значения коэффициентов. В частности, в узлах интерполяции можно задать не только значения функции, но и значения ее производной. В противном случае, задача интерполирования не имеет решения в общем виде, т.к. система условий может оказаться несовместной. В этом случае задача интерполирования заменяется задачей общей аппроксимации, которая заключается в построении многочлена низшей степени, наименее отклоняющегося от заданной функции.

Интерполяционный полином Лагранжа

Примером наипростейшей базисной системы функций можно считать систему ,,…,,..

Утверждение 1.Если два многочлена степени принимают одинаковые значения при различных значениях переменной, то эти многочлены равны.

Пусть многочлены истепени‑ такие попарно различные числа, что. Рассмотрим многочлен. Очевидно, что степеньне превосходитлибо‑ нулевой многочлен, причем, т.е. многочленимеетразличных корней, что невозможно. Следовательно,и.

Это утверждение позволяет доказать следующую теорему.

Теорема.Для каждого натурального числа существует один и только один многочлен степени, который принимает любые наперед заданные значения призначениях неизвестной.

Пусть ‑ различные числа‑ произвольные числа. Построим многочленстепенитакой, что. По утверждению 1, он определен однозначно:

.

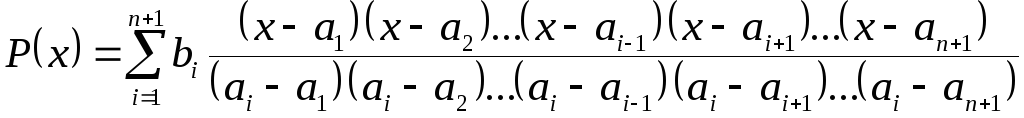Степень , и, очевидно,. Многочлен (1) называетсяинтерполяционным многочленом Лагранжа.

Пример. Построить интерполяционный многочлен Лагранжа по заданной таблице значений:

.