2.2. Вычисление двойного интеграла.

Определение 2. Правильной в направлении оси Oу областью D называется область, удовлетворяющая следующим условиям:

1. Верхняя и нижняя её границы описываются уравнениями исоответственно;

2. Прямые пересекают её верхнюю и нижнюю границы не более чем в двух точках.

Аналогично определяется правильная область в направлении осиOx.

Формулу для вычисления ДИ выведем, исходя из его геометрического смысла.

П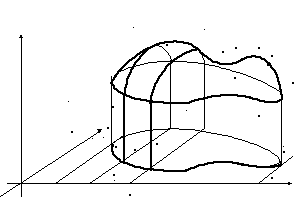усть областьD является правильной областью. Пересечем цилинд-рическое тело с нижним основанием – областью D, а верхним – поверх-ностью , плоскостямиx и :

z

y

O x

a x b

Фиксируя x, вычислим интеграл , значение которого равно площади криволинейной трапеции, полученной в сечении плоскостью. Если это выражение умножить наи проинтегрировать отa до b, то из рисунка следует, что

,

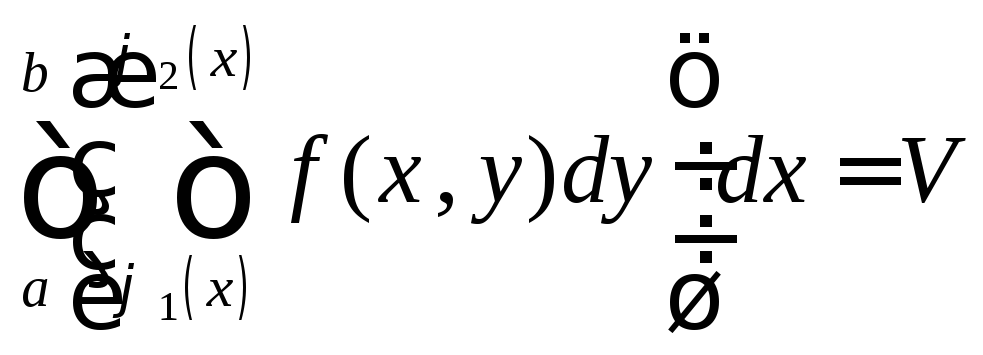где V  объём данной цилиндрической области.

Таким образом, получаем формулу для вычисления ДИ

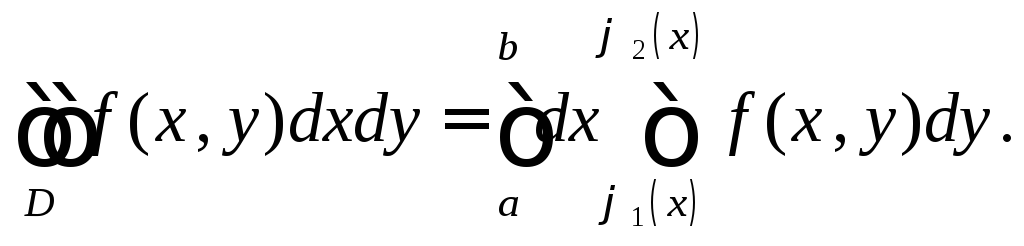(5)

Замечание 3. Если область правильная в направлении оси Ox, то

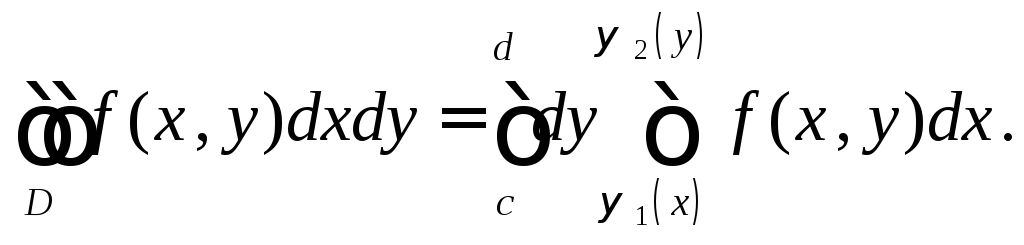(6)

у

d

c

O x

Замечание 4. Если область неправильная, то её прямыми разбивают на ряд правильных областей и тогда ДИ по такой области равен сумме двойных интегралов по правильным областям.

П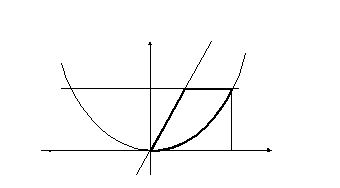ример. Вычислить ДИ по области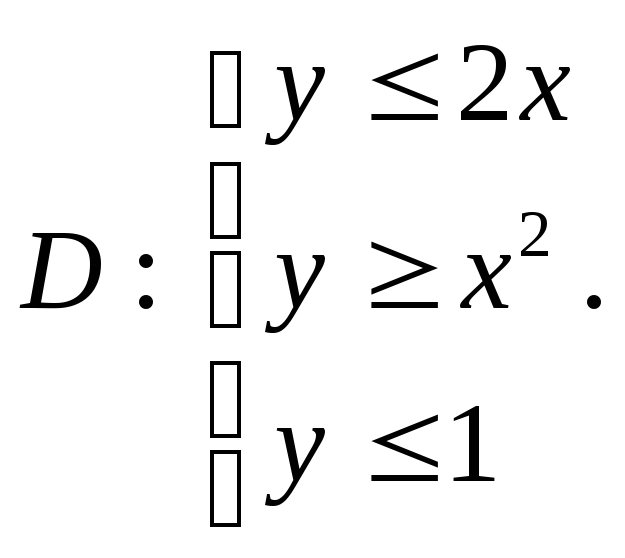

Изобразим данную область на рисунке

у

D

O 1 x

Для такой области более удобно для вычисления ДИ использовать формулу (6) (почему?)

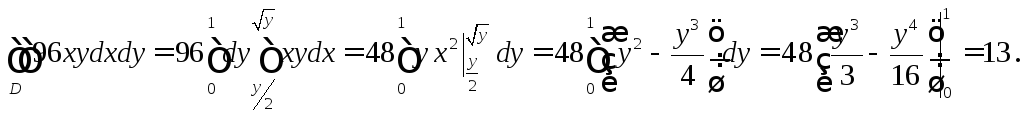
Лекция № 53

2.3. Замена переменных в двойном интеграле.

Пусть координаты х и у являются функциями новых переменных и и v:

(1)

где иоднозначные и непрерывные функции вместе со своими производными в некоторой области. По формуле (1) каждой точкесоответствует единственная точка.

Верно и обратное.

Таким образом, между областямиD и установлено взаимно однозначное соответствие. Каждой линии видасоответствуют некоторые кривые в плоскостиOxy, а прямоугольной площадке  криволинейная площадка в областиD.

v y

M

v

D

u x

O u O

Рассмотрим интегральную сумму от функции в области

(2)

В формуле (2), чтобы получить интегральную сумму по области , необходимо выразитьчерез. Если вычислять как площадь параллелограмма, то с точностью до б.м.в. более высокого порядка можно получить равенство, где определительназывается якобианом. Тогда равенство (2) принимает вид

. (3)

Переходя к пределу при в интегральных суммах (3), получаем

. (4)

Формула (4) представляет собой формулу замены переменных в ДИ.

Замечание 1. Так как 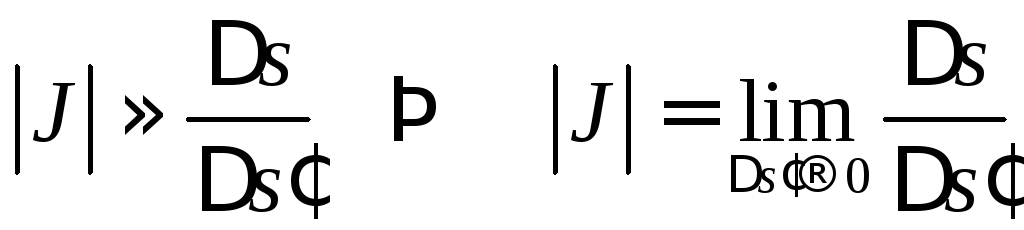, то якобиан представ-ляет собой коэффициент изменения площади элементарной площадки.