5.2. Поверхностные интегралы второго рода

Пусть в каждой точке определён некоторый вектор. Разобьём поверхность на элементарные площадкии составим интегральную сумму

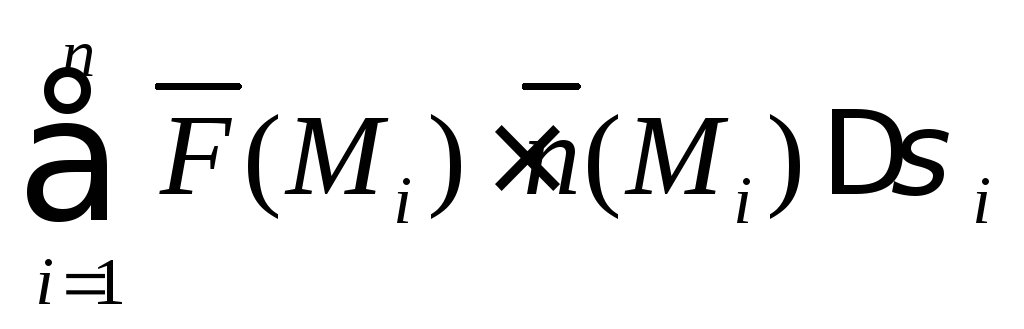, (1)

где  единичный нормальный вектор поверхности.

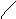
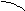
Переходя к пределу в интегральной сумме (1), получаем определение поверхностного интеграла второго рода:

.

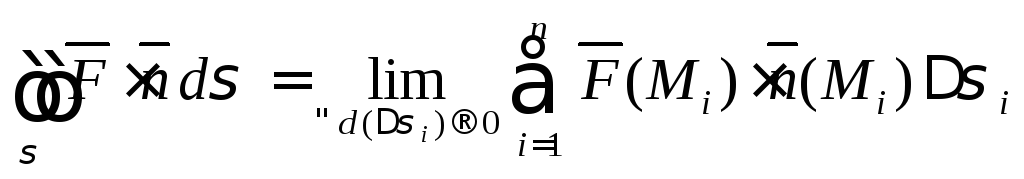Из определения поверхностного интеграла второго рода следует:

1. Свойства интеграла аналогичны свойствам 1-2 кратных интегралов.

2. При изменении стороны поверхности интеграл меняет знак, так как меняет свое направление нормальный вектор.

Так как

и , то

-

другая запись поверхностного интеграла второго рода.

Если уравнение поверхности , то

,

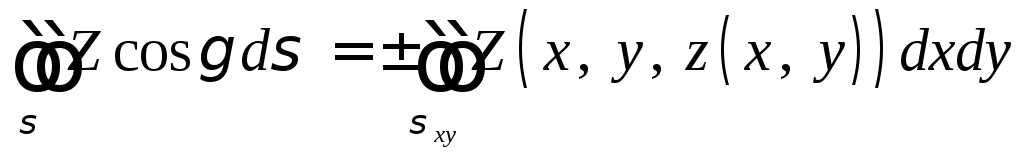где - проекцияв плоскостьОху, а знак перед интегралом берётся “+“, если и ““, если . Аналогично вычисляются инте-гралы.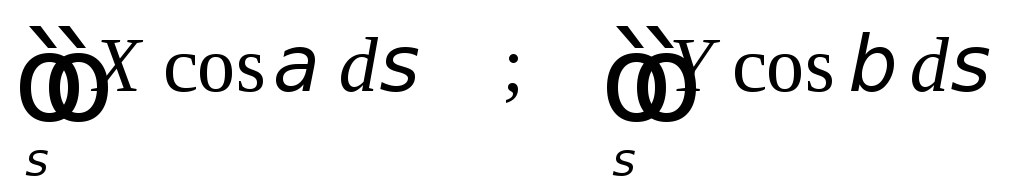

Пример 4. Вычислить , если, а поверхность грань АОС пирамиды АВСО, образованной пересече-нием плоскости с координатными плоскостями.

В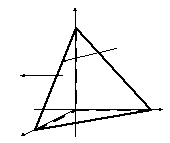этом случае.z

. С

Тогда и

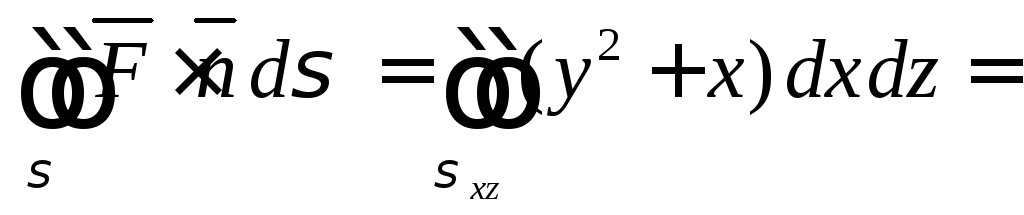
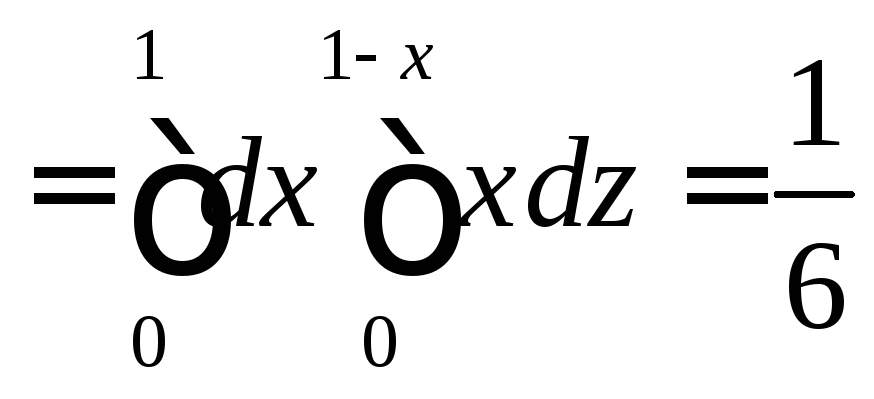. О В у

А

х

5.3. Приложения поверхностных интегралов

Приложения поверхностных интегралов первого рода к задачам гео-метрии и механики аналогичны приложениям тройных интегралов, если заменить .

Пример 5. Определить момент инерции однородной полусферы радиуса R относительно ее центра.

Так как

,

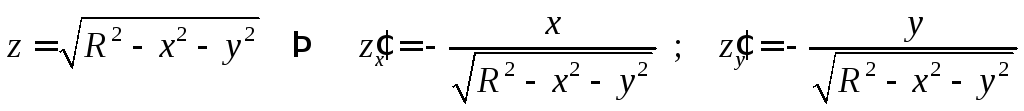то получим

,

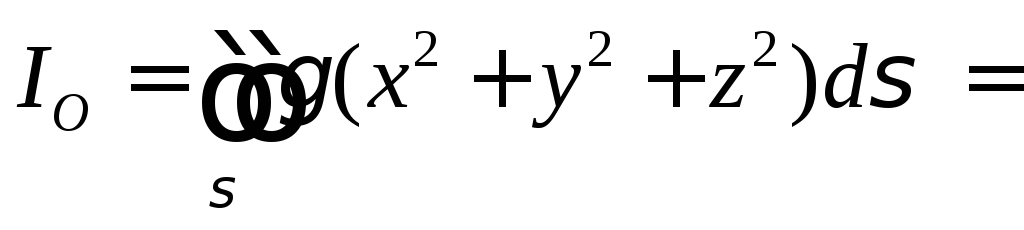
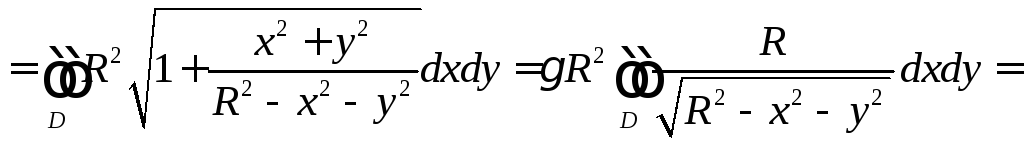
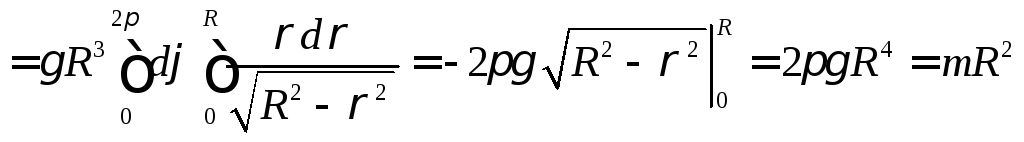где  масса полусферы.

Если  вектор скоростей жидкости, протекающей через поверхность , то интеграл

представляет собой количество жидкости, протекающей через эту поверх-ность за единицу времени (поток через поверхность) – физический смысл поверхностного интеграла второго рода.

Лекция № 58. Тема 6 : Элементы теории поля

6.1. Понятие поля

Определение 1. Полем называется область пространства, в каждой точке которой определено рассматриваемое значение физической характеристики среды.

Эти характеристики могут быть скалярными (например, температура, давление, плотность и т.д.) или векторными (скорость, сила и т.д.).

Соответственно и поля называются скалярными и векторными.

Для задания скалярного поля достаточно задать одну функцию . Для задания векторного полянеобходимо задать три скалярные функции:

Геометрические образы поля позволяют наглядно представить его структуру. Геометрическими образами скалярного поля являются поверхности уровня (в трёхмерном пространстве) или линии уровня (в двумерном пространстве). Они соответственно задаются уравнениями: ,

Для векторного поля геометрическими образами являются векторные линии – такие линии, в каждой точке которых в данный момент времени касательная совпадает с направлением вектора поля.

М

Пусть уравнение векторной линии имеет вид

Тогда из условия коллинеарности вектора касательной и поляполучаем систему дифференциальных уравнений для определения векторных линий

.

Пример 1. Найти уравнение векторных линий поля скоростей, вращающегося тела с постоянной угловой скоростью

В этом случае

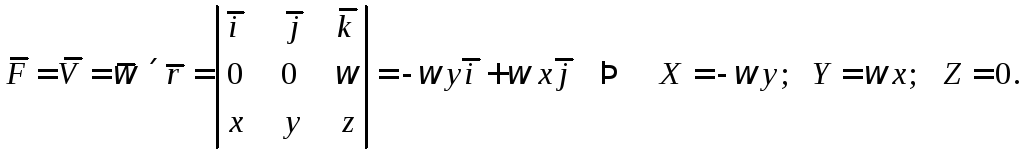
Тогда или множество концентрических окружностей,