7.2. Теорема Чебышева

Теорема. Если  независимые СВ, имеющие конечные дисперсии, т.е. , то

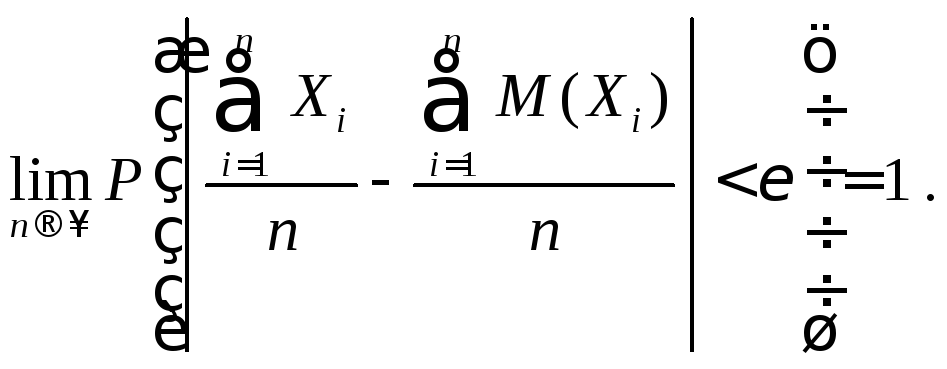
Рассмотрим новую случайную величину 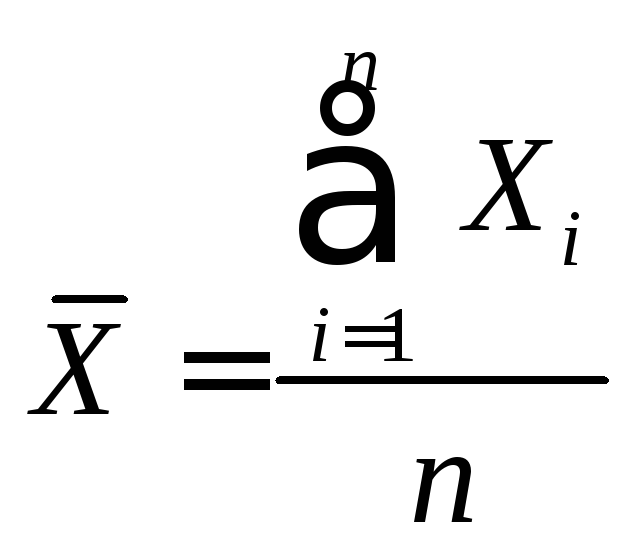и применим к ней неравенство Чебышева

.

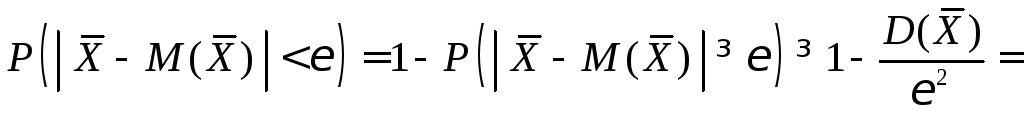
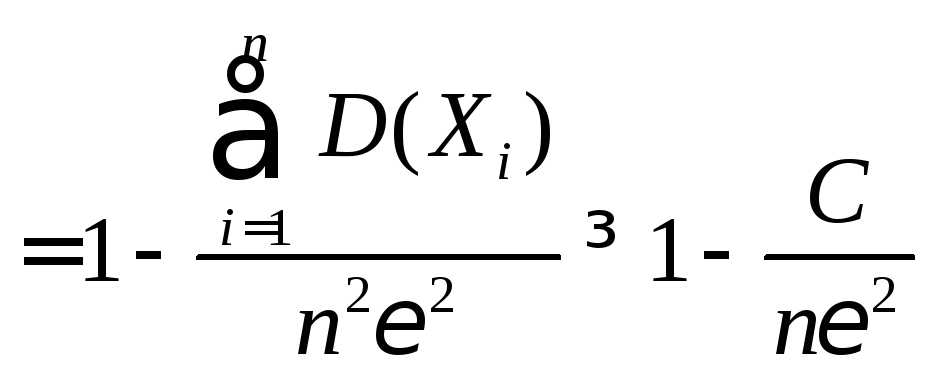Переходя к пределу при и, учитывая что, получаем теорему Чебышева.

Следствия:

1. Теорема Бернулли. Если  число наступления события А в п независимых испытаниях, а р  вероятность А, то

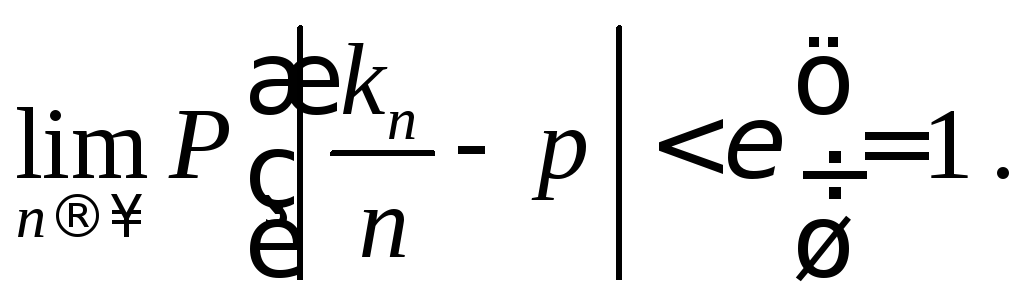
Пусть  число появления события A в одном испытании, т.е.

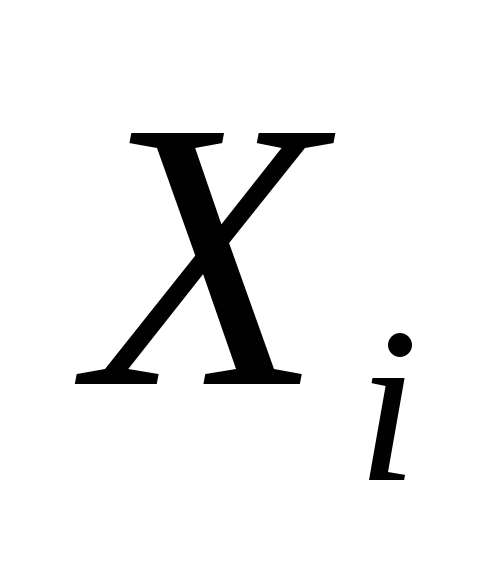
	0	1
p	q	p

Тогда и

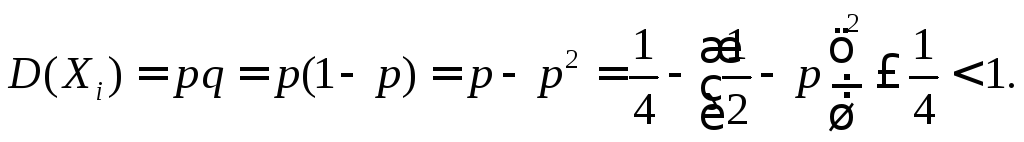
Полагая в неравенстве Чебышева соответствующие значения, получаем теорему Бернулли.

2. Если для последовательности независимых случайных величин вы-полняется равенство

,

то

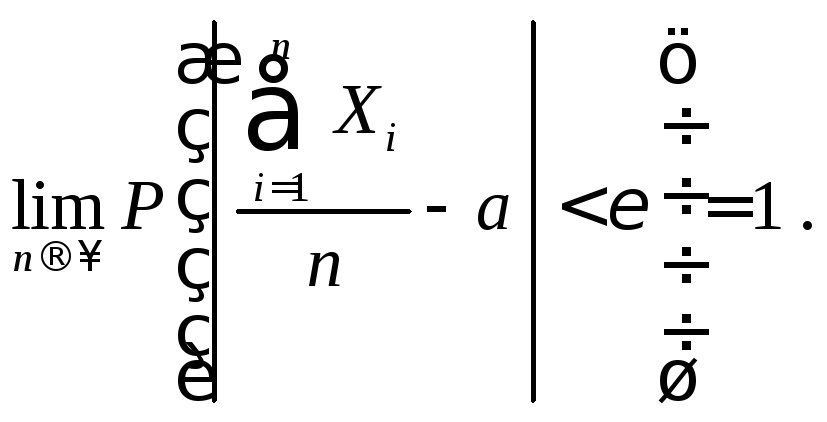
Доказательство следует из теоремы Чебышева.

Этот частный случай даёт основание правилу среднего арифмети-ческого, употребляемого в теории измерений, т.е. если результаты изме-рений: , то искомая величина.

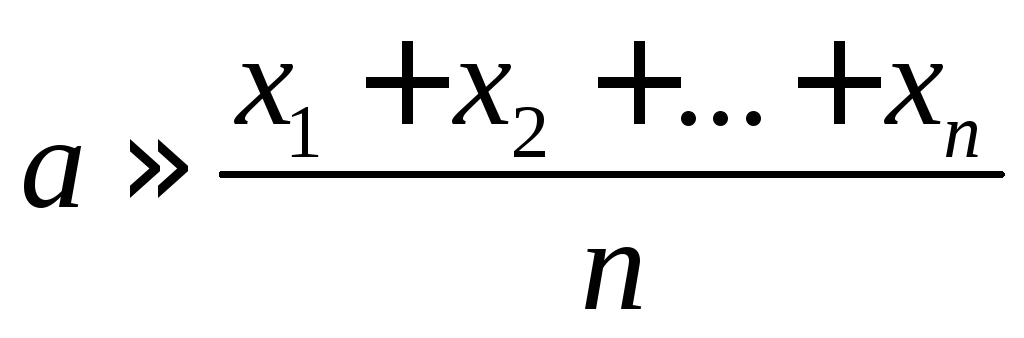Следовательно, увеличивая количество измерений, мы будем получать более надежный результат.

Пример 3. Дисперсия каждой из попарно независимых случайных величин не превышает 10. Оценить вероятность того, что отклонение среднего арифметического 16000 этих величин от среднего арифметического их математических ожиданий не превосходит 0,25.

По условию

Тогда по теореме Чебышева С = 10 и искомая вероятность

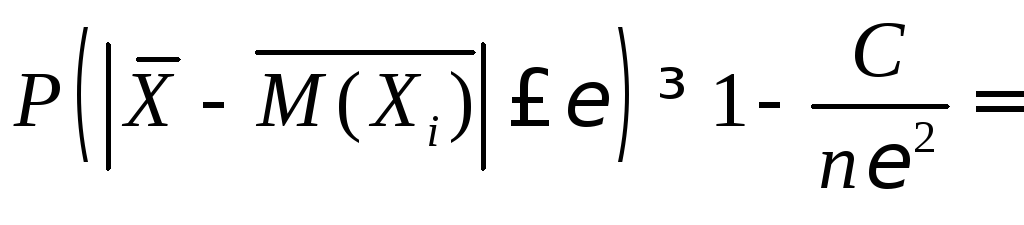
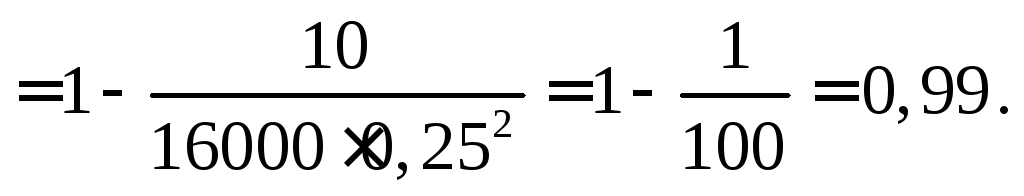
Лекция № 67. Тема 8 : Многомерные случайные величины

8.1. Многомерные св и их функции распределения

Определение 1. Многомерной случайной величиной называется вектор, координаты которого являются СВ, т.е. .

Например, координаты точки попадания при выстреле – двумерная СВ; станок производит детали длиной X, внутренним диаметром Y, внеш-ним диаметром Z - трёхмерная СВ (X, Y, Z).

Ограничимся случаем двумерной СВ (X, Y). Законом распределения дискретной двумерной СВ является перечень её возможных значений и соответствующих им вероятностей. Его удобно задавать в виде таблицы

Y X			…
			…
			…
…	…	…	…	…
			…

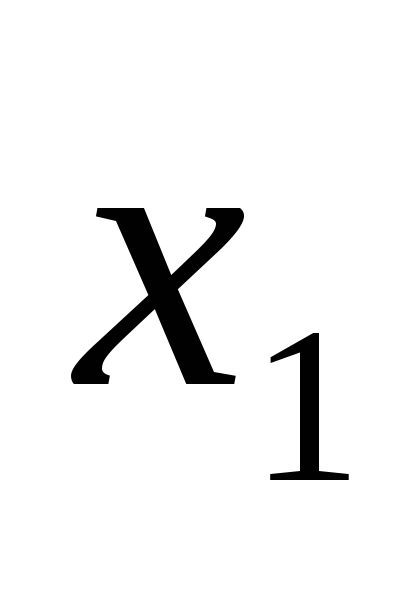
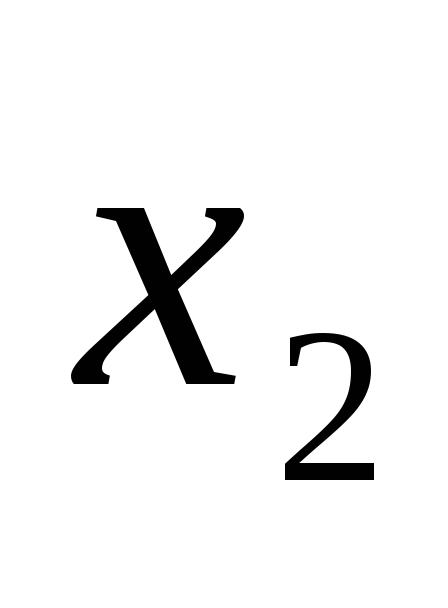
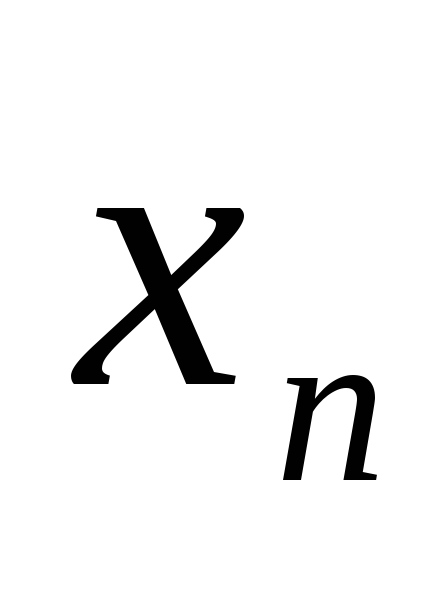
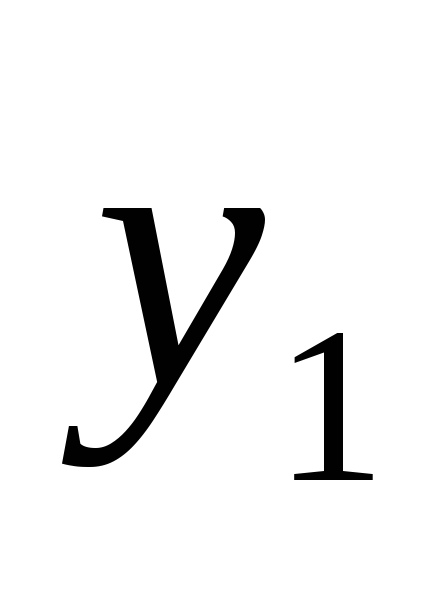
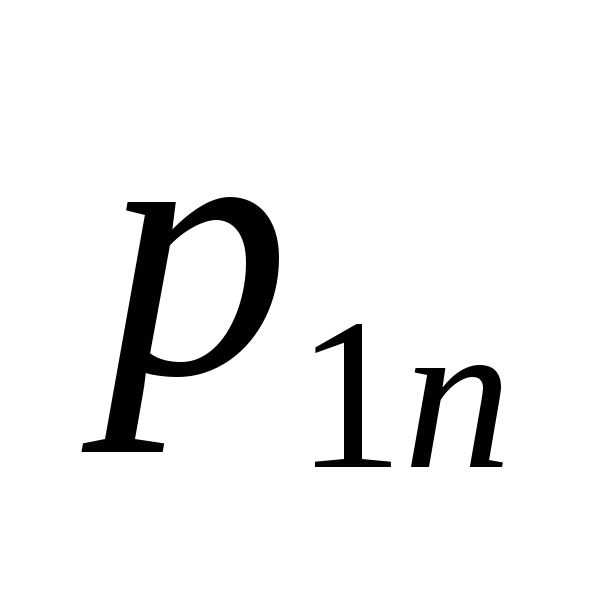
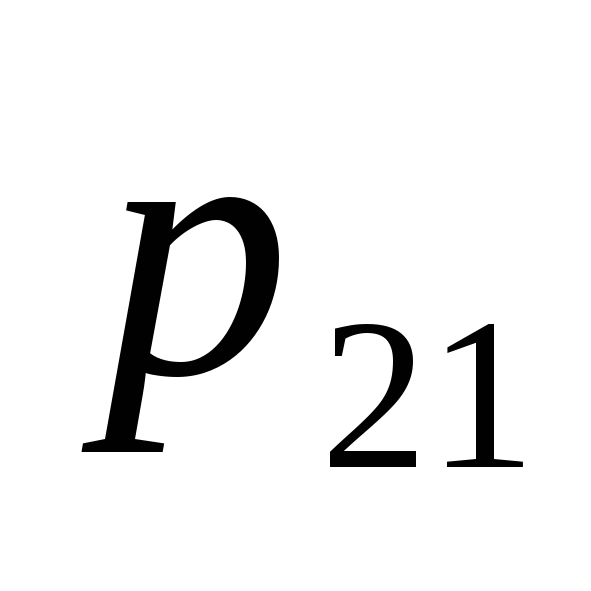
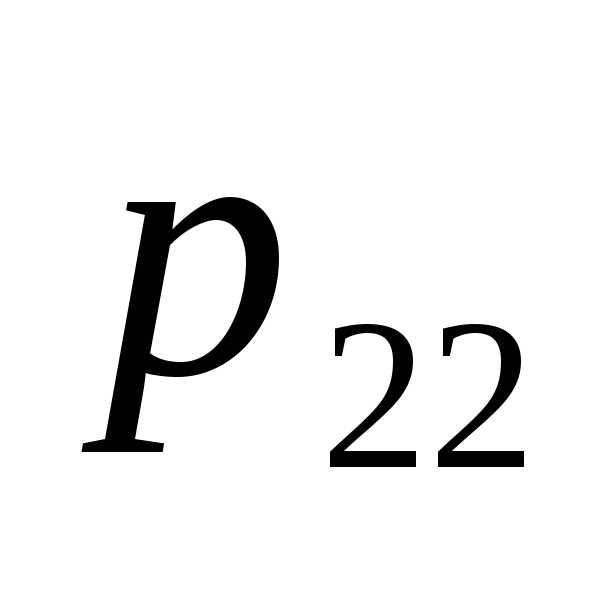
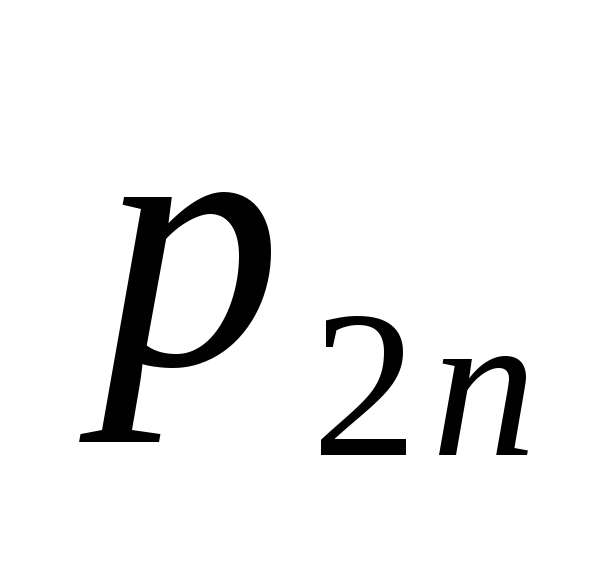
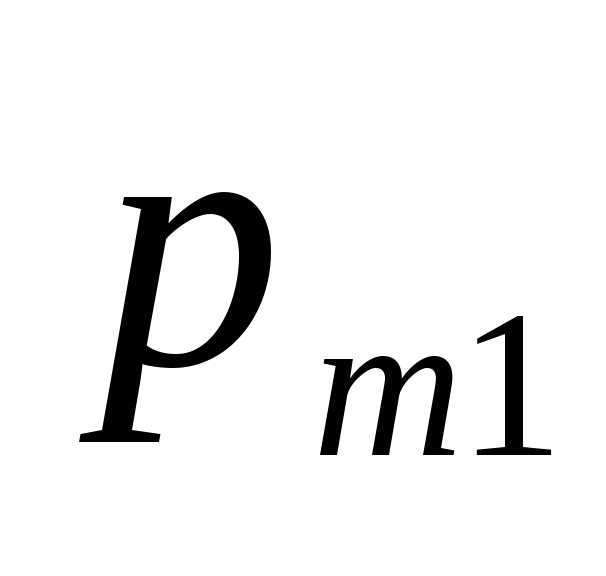
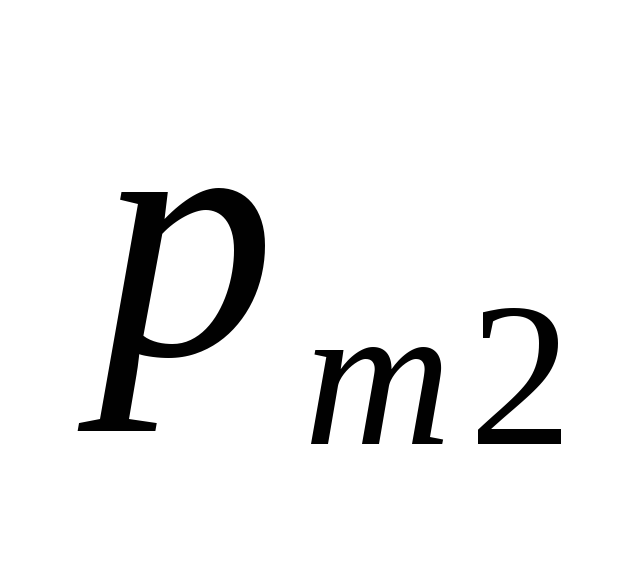
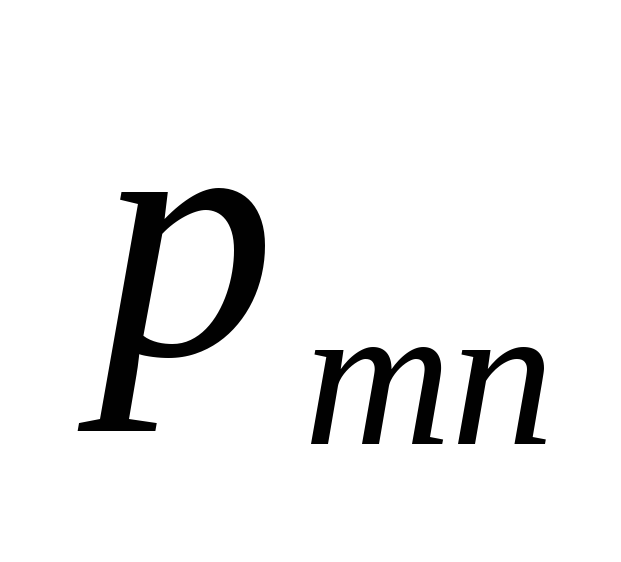
Здесь .

Аналогично, как и в случае одномерной СВ, обозначим через  множество элементарных событий, для которых одно-временно выполняются неравенства и.

Определение 2. Функцией распределения двумерной СВ называется .

Геометрически представляет собой вероятность попадания СВ (X, Y) в бесконечный квадрат с вершиной в точке (х, у).

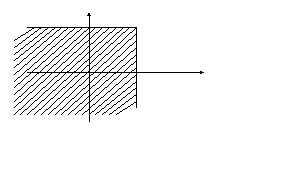
у

(х, у)

х

Из определения функции распределения следуют ее свойства.

1.

2.  неубывающая функция.

3.

4. , где и функции распределения СВ X и Y соответственно.

5.

Рассмотрим предел

.

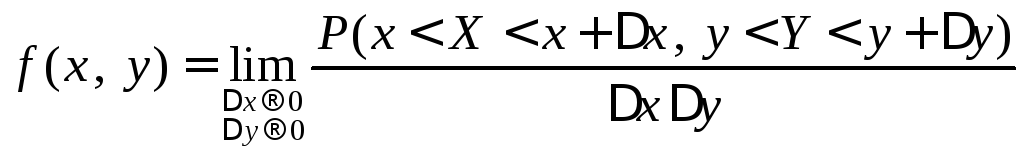Можно показать, что этот предел равен  плот-ности распределения двумерной СВ.

Свойства плотности распределения:

1. , так какнеубывающая функция.

2. Вероятность попадания СВ (X, Y) в область D равна

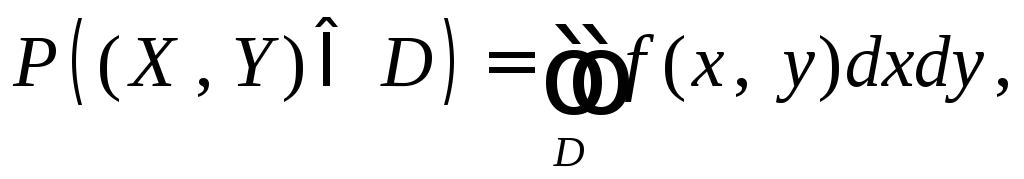
так как  вероятность попадания в прямоугольник пло-щадью .

3. 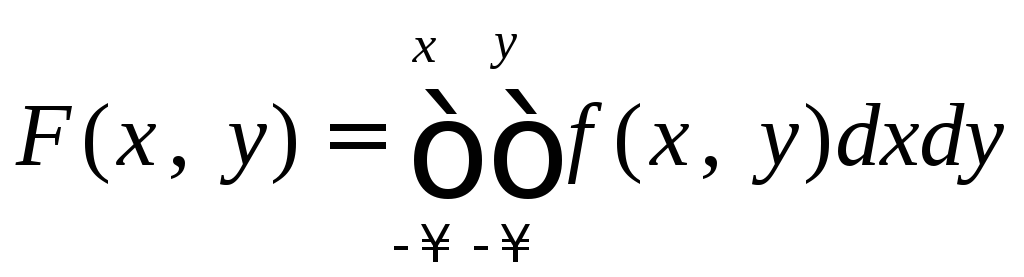, что следует из определения.

4. 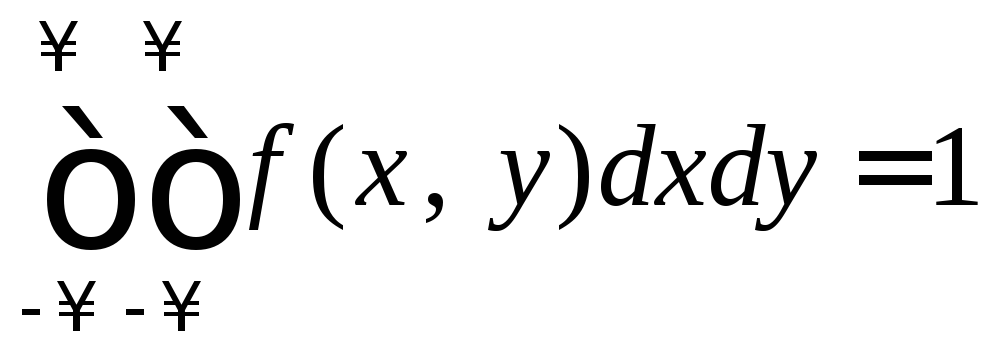, что следует из свойства3 и того, что

5.

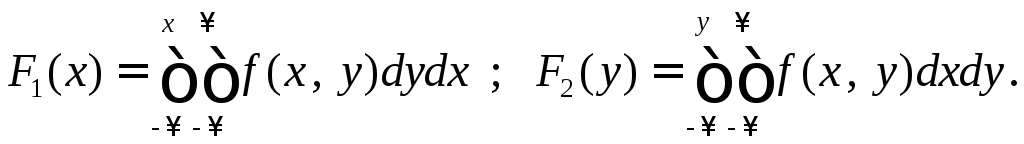
Определение 3. Случайные величины X и Y называются независи-мыми, если выполняется равенство

или

Пример 1. Определить зависимы или независимы СВ X, Y и найти вероятность их попадания в квадрат , если

.

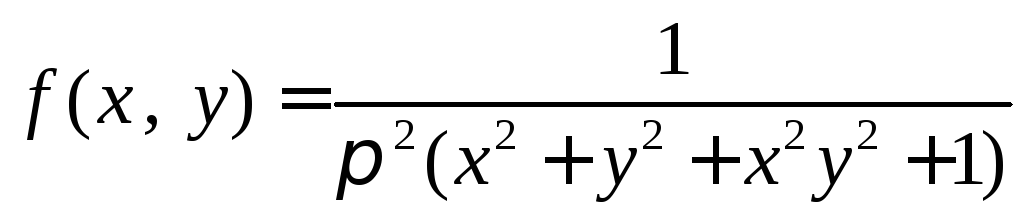Имеем

X и Y - независимые СВ.