
- •Лекция № 45. Тема 1 : Числовой ряд. Необходимый признак сходимости
- •1.2. Необходимый признак сходимости. Гармонический ряд
- •Тема 2 : Достаточные признаки сходимости рядов с положительными членами
- •2.1. Признаки сравнения
- •Лекция № 46
- •2.2. Признак Даламбера
- •2.3. Радикальный признак Коши
- •2.4. Интегральный признак Коши
- •Тема 3 : Знакопеременные ряды
- •3.1. Знакочередующиеся ряды. Теорема Лейбница
- •3.2. Абсолютная и условная сходимость
- •Лекция № 47. Тема 4 : Функциональные ряды
- •4.1. Определение функционального ряда
- •4.2. Равномерная сходимость функциональных рядов
- •Тема 5 : Степенные ряды
- •5.1. Определение степенного ряда. Теорема Абеля
- •Лекция № 48
- •5.2. Разложение функций в степенные ряды
- •5.3. Применение рядов Тейлора
- •Лекция № 49. Тема 6 : Ряды Фурье
- •6.1. Определение ряда Фурье
- •6.2. Условия разложения функции в ряд Фурье
- •Лекция № 50
- •6.4. Ряды Фурье для четных и нечетных функций
- •6.5. Разложение непериодических функций в ряд Фурье
- •6.6. Интеграл Фурье
- •Уравнения математической физики Лекция № 51.
- •1. Основные типы уравнений математической физики
- •2. Решение волнового уравнения методом Фурье
- •Кратные интегралы Лекция № 52. Тема 1: Определение кратного интеграла
- •1.1. Задачи, приводящие к понятию кратного интеграла
- •1.2. Определение кратного интеграла и его основные свойства
- •Тема 2: Двойной интеграл
- •2.1. Определение двойного интеграла (ди)
- •2.2. Вычисление двойного интеграла.
- •Лекция № 53
- •2.3. Замена переменных в двойном интеграле.
- •2.4. Ди в полярной системе координат
- •2.5. Приложения двойного интеграла
- •Лекция № 54
- •Лекция № 55. Тема 3 : Тройной интеграл
- •3.1. Определение и вычисление тройного интеграла
- •3.2. Замена переменных в тройном интеграле
- •3.3. Приложения тройного интеграла
- •Лекция № 56. Тема 4 : Криволинейные интегралы
- •4.1. Криволинейные интегралы первого рода или по длине дуги
- •4.2. Криволинейные интегралы второго рода или по координатам
- •Лекция № 58.
- •4.3. Формула Грина
- •4.4. Условие независимости криволинейного интеграла второго рода от пути интегрирования
- •Тема 5 : Поверхностные интегралы
- •5.1. Поверхностные интегралы первого рода
- •5.2. Поверхностные интегралы второго рода
- •5.3. Приложения поверхностных интегралов
- •Лекция № 58. Тема 6 : Элементы теории поля
- •6.1. Понятие поля
- •6.2. Формула Гаусса Остроградского
- •6.3. Формула Стокса
- •Теория вероятностей Лекция № 59. Тема 1 : Общие понятия
- •1.1. Предмет теории вероятностей
- •1.2. Пространство элементарных событий
- •1.3. Операции над событиями
- •1.4. Статистический подход к понятию вероятности
- •Лекция № 60
- •1.5. Элементы комбинаторики
- •1. Перестановки.
- •2. Сочетания.
- •3. Размещения.
- •1.6. Классическое определение вероятности
- •1.7. Аксиоматическое определение вероятности
- •Лекция № 61. Тема 2 : Основные теоремы теории вероятностей
- •2.1. Теорема умножения вероятностей
- •2.2. Теорема сложения вероятностей
- •2.3. Формула полной вероятности
- •2.4. Формула Бейеса
- •Лекция № 62. Тема 3 : Повторение испытаний
- •3.1. Независимые испытания. Формула Бернулли
- •3.2. Локальная теорема Муавра – Лапласа
- •3.3. Интегральная теорема Лапласа
- •3.4. Теорема Пуассона
- •3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях
- •Лекция № 63.
- •Тема 4 : Случайные величины и функции распределения
- •4.1. Случайные величины
- •4.2. Функция распределения вероятностей для дискретной св
- •4.3. Непрерывная св. Функция распределения
- •Лекция № 64. Тема 5 : Числовые характеристики св
- •5.1. Математическое ожидание св
- •5.2. Дисперсия и среднее квадратическое отклонение св
- •5.3. Понятие о моментах св
- •Лекция № 65. Тема 6 : Основные законы распределения св
- •6.1. Законы распределения дискретных случайных величин
- •6.1.1. Биномиальное распределение
- •6.1.2. Распределение Пуассона
- •6.1.3. Геометрическое распределение
- •6.2. Законы распределения непрерывных случайных величин
- •6.2.1. Равномерное распределение
- •6.2.2. Показательное распределение
- •Лекция 66
- •6.2.3. Нормальное распределение
- •Тема 7 : Закон больших чисел
- •7.1. Неравенство Чебышева
- •7.2. Теорема Чебышева
- •Лекция № 67. Тема 8 : Многомерные случайные величины
- •8.1. Многомерные св и их функции распределения
- •8.2. Числовые характеристики двумерной св
- •Элементы математической статистики Лекция № 68. Введение
- •1. Предмет математической статистики
- •Тема 1: Статистические законы распределения выборки
- •1.1. Полигон и гистограмма
- •1.2. Эмпирическая функция распределения
- •Тема 2 : Статистические оценки параметров распределения
- •2.1. Точечные оценки
- •2.2. Интервальные оценки
- •Лекция № 69
- •Тема 3 : Проверка статистических гипотез. Критерий согласия Пирсона
- •Тема 4 : Элементы теории корреляции
- •4.1. Статистические зависимости
- •4.2. Линейная регрессия
- •4.3. Корреляционная таблица
- •4.4. Выборочный коэффициент корреляции
Лекция № 47. Тема 4 : Функциональные ряды
4.1. Определение функционального ряда
Определение 1. Ряд, члены которого являются функциями, называется функциональным рядом, т.е. это ряд вида
 ,
(1)
,
(1)
где
![]() являются непрерывными функциями в
областиD.
являются непрерывными функциями в
областиD.
Определение 2. Множество значений x, при которых ряд (1) сходится, называется областью сходимости данного ряда.
Пример 1.
Найти область сходимости ряда
 .
.
Замечаем, что ряд содержит только положительные члены, поэтому применим признак Даламбера
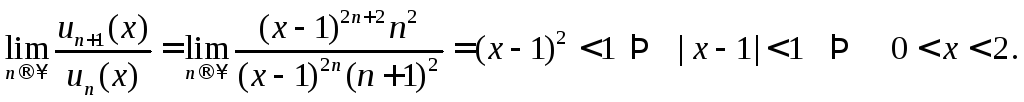
Исследуем на концах
интервала

ряд сходится. Область сходимости
ряд сходится. Область сходимости
![]() .
.
Аналогично, как и для числовых рядов, определяется сумма и остаток ряда
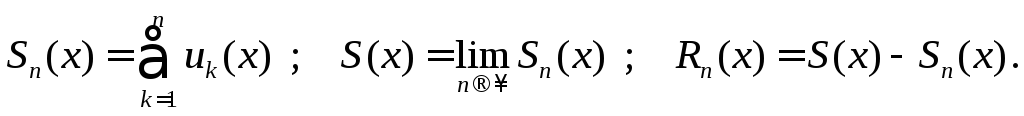
При этом, если
ряд сходится, то
![]() .
.
4.2. Равномерная сходимость функциональных рядов
Определение 3.
Функциональный ряд (1) равномерно сходится
в некоторой области D
к своей сумме
![]() ,
если
,
если![]() ,
что при
,
что при![]() для всех
для всех![]() .
.
Для определения равномерной сходимости удобно использовать
Критерий равномерной сходимости (теорема Вейерштрасса). Если все члены ряда (1) удовлетворяют неравенству
![]() (2)
(2)
для любого x
из некоторой области D
и ряд
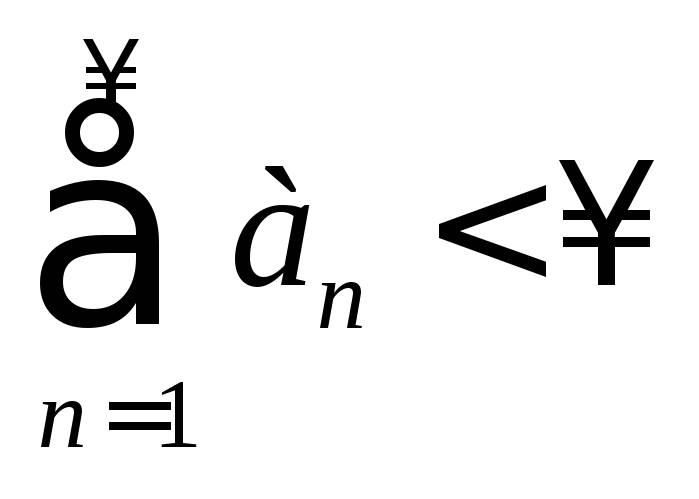 ,
то ряд (1) сходится равномерно в этой
области.
,
то ряд (1) сходится равномерно в этой
области.
Пример 2.
Исследовать на равномерную сходимость
ряд
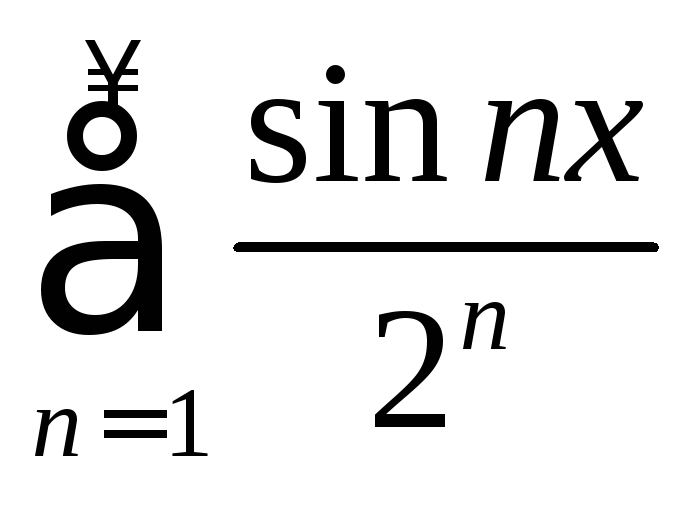 .
.
Так как
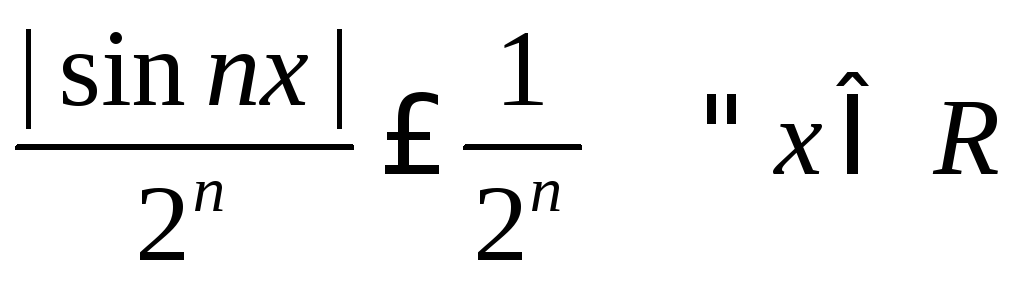 и ряд
и ряд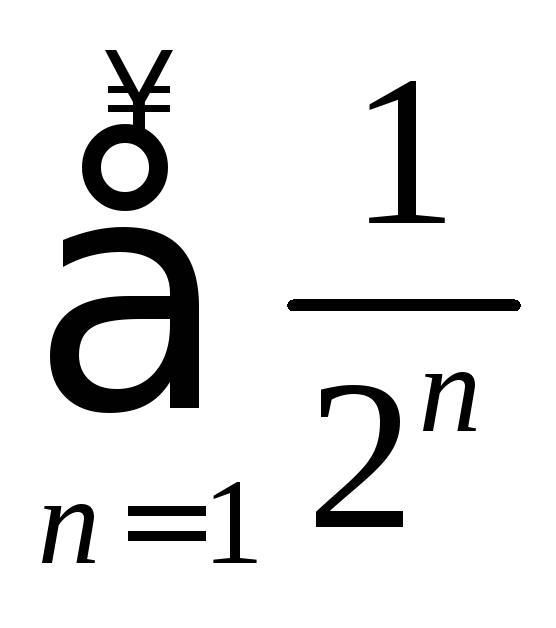 сходится, то ряд
сходится, то ряд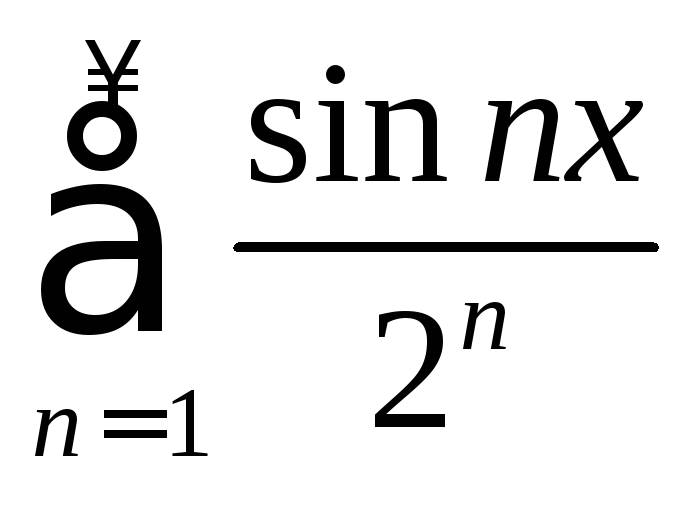 сходится равномерно
сходится равномерно![]()
Основные свойства равномерно сходящихся рядов:
1. Сумма равномерно
сходящегося ряда из непрерывных функций
на
![]() есть функция непрерывная в этой
области.
есть функция непрерывная в этой
области.
2. Равномерно
сходящийся ряд из непрерывных функций
на
![]() можно почленно интегрировать и
дифференцировать, если ряд, состав-ленный
из производных, сходится равномерно.
можно почленно интегрировать и
дифференцировать, если ряд, состав-ленный
из производных, сходится равномерно.
Тема 5 : Степенные ряды
5.1. Определение степенного ряда. Теорема Абеля
Определение 4. Функциональный ряд вида
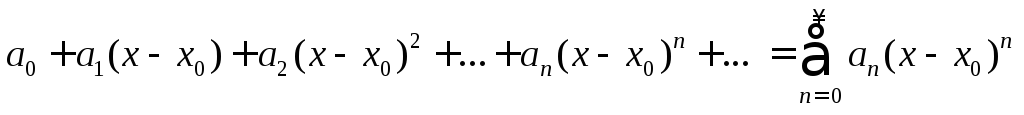 (2)
(2)
называется степенным рядом, где
![]() члены ряда;
члены ряда;
![]() коэффициенты
ряда.
коэффициенты
ряда.
Замечание 1.
Путём замены
![]() ряд (2) принимает вид
ряд (2) принимает вид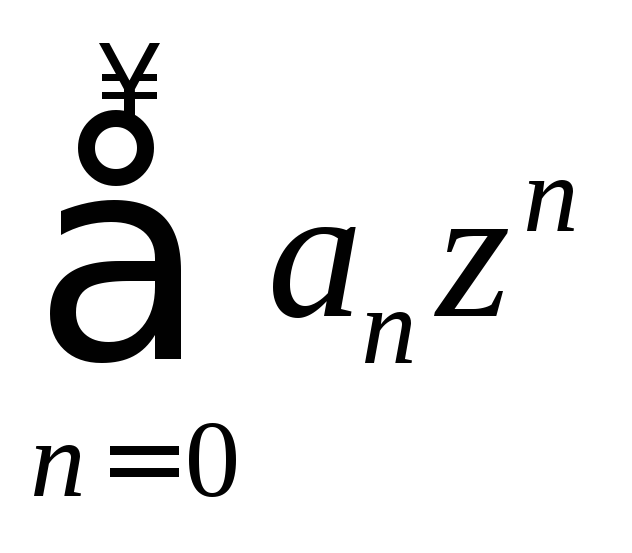 ,
поэтому в дальнейшем можно считать,
что
,
поэтому в дальнейшем можно считать,
что![]() и рассматривать ряд
и рассматривать ряд
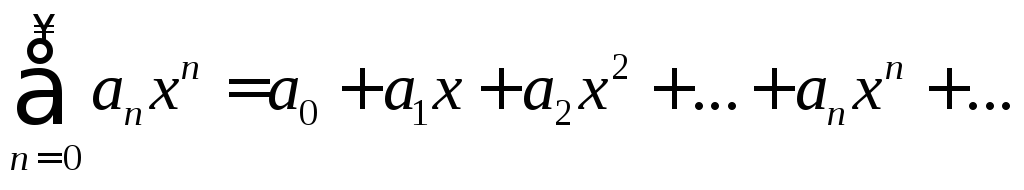 .
(3)
.
(3)
Теорема Абеля.
Если степенной ряд (3) сходится при
некотором значении
![]() ,
то он является сходящимся и причем
абсолютно
,
то он является сходящимся и причем
абсолютно![]()
- если ряд (3)
расходится при некотором
![]() ,
то он расходится
,
то он расходится![]()
Так как ряд
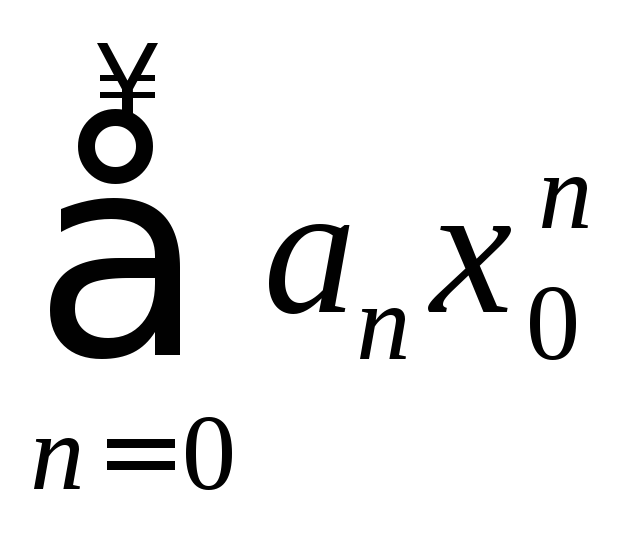 сходится, то
сходится, то![]() и
и![]() .
.
Преобразуем ряд (3):
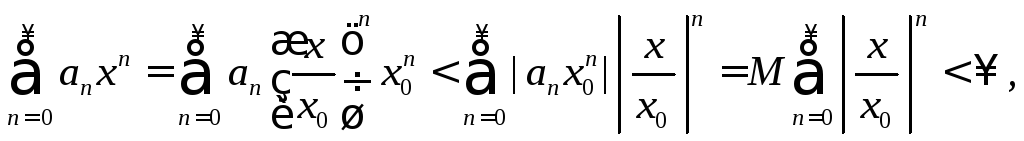
так как
 и ряд, как сумма бесконечно убывающей
геометри-ческой прогрессии, сходится
и причем абсолютно.
и ряд, как сумма бесконечно убывающей
геометри-ческой прогрессии, сходится
и причем абсолютно.
Пусть при некотором
![]() ряд (3) расходится. Тогда он будет
расходиться при
ряд (3) расходится. Тогда он будет
расходиться при![]() .
Действительно, если бы в какой либо
точке х
ряд сходился, то из выше доказанного,
он сходился бы и при
.
Действительно, если бы в какой либо
точке х
ряд сходился, то из выше доказанного,
он сходился бы и при
![]() ,
что по условию теоремы невозможно. Это
противоречие доказывает вторую часть
теоремы.
,
что по условию теоремы невозможно. Это
противоречие доказывает вторую часть
теоремы.
Следствие. Теорема Абеля позволяет определить расположение точек сходимости и расходимости степенного ряда: областью сходимости является интервал с центром в начале координат.
Определение.5.
Число
![]() называется радиусом сходимости
сте-пенного ряда, если ряд сходится при
называется радиусом сходимости
сте-пенного ряда, если ряд сходится при![]() и расходится при
и расходится при![]() ,
а интервал
,
а интервал![]() называется интервалом сходимости.
называется интервалом сходимости.
Из теоремы следует,
что интервалы сходимости рядов
 и
и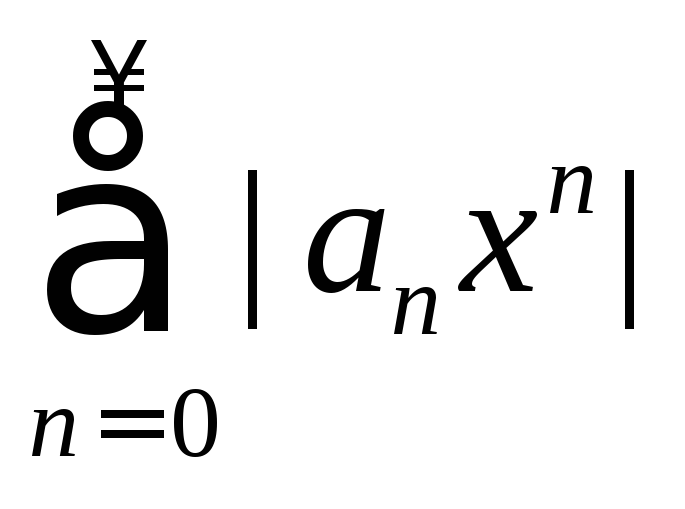 совпадают. Тогда по признаку Даламбера
получаем
совпадают. Тогда по признаку Даламбера
получаем
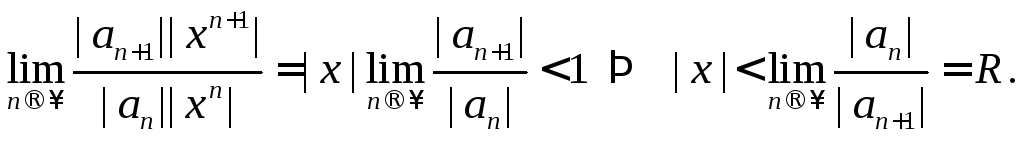
Окончательно,
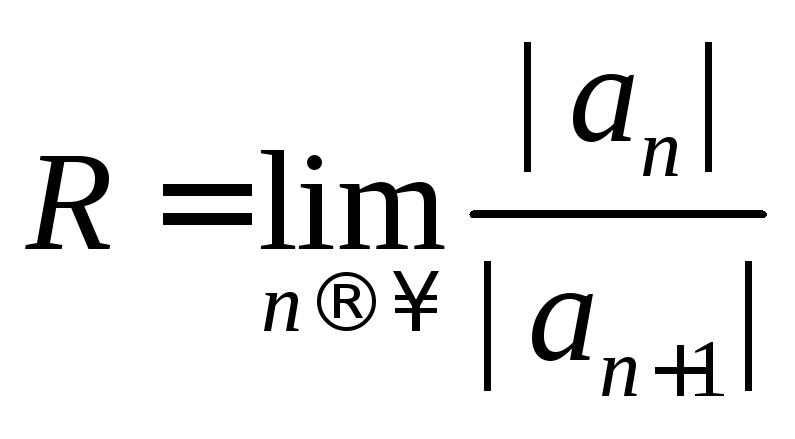 .
.
Аналогично,
используя радикальный признак Коши,
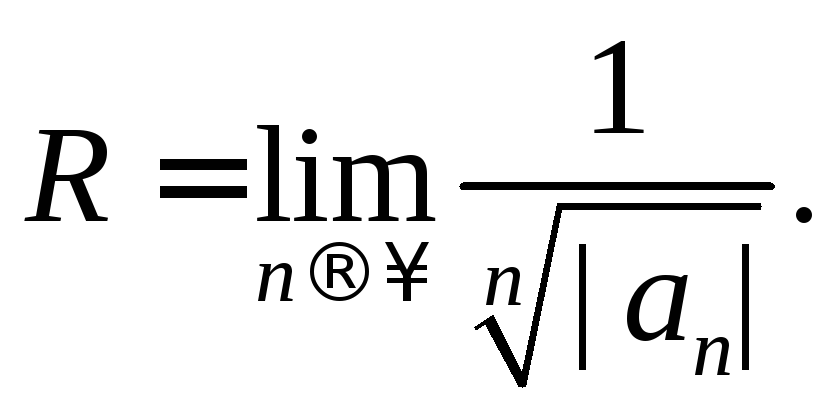
Замечание 2. Для нахождения области сходимости степенного ряда вначале необходимо найти интервал сходимости или непосредственно или по формуле вычислить радиус сходимости, а затем исследовать сходимость на концах интервала.
Из теоремы следуют свойства степенных рядов:
1. Степенной ряд сходится равномерно на любом отрезке, принад-лежащем интервалу сходимости.
2. В интервале сходимости степенной ряд сходится к непрерывной функции и его можно почленно интегрировать и дифференцировать. При этом ряд, составленный из производных, имеет тот же радиус сходимости, что и данный ряд.
Пример 3.
Найти область сходимости степенного
ряда
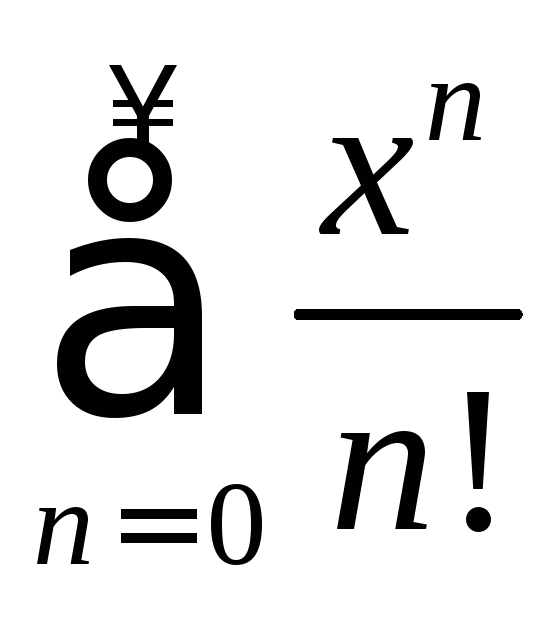 .
.
Вычислим
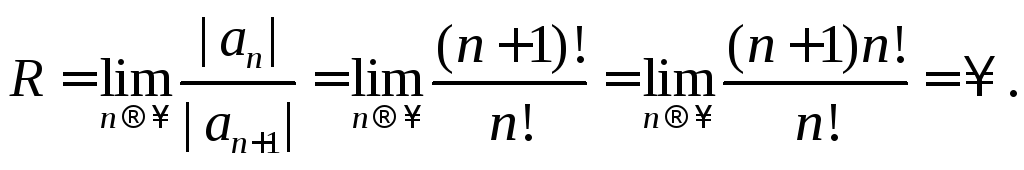
Область сходимости
совпадает с интервалом сходимости
![]()
Пример 4.
Найти область сходимости степенного
ряда
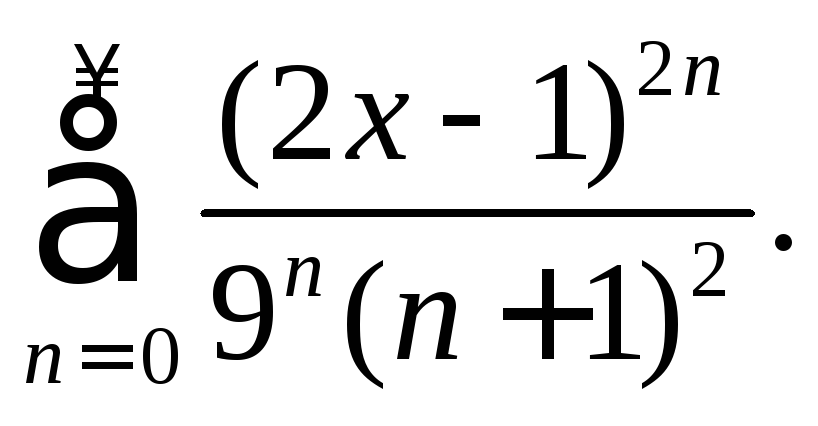
Воспользуемся общим подходом
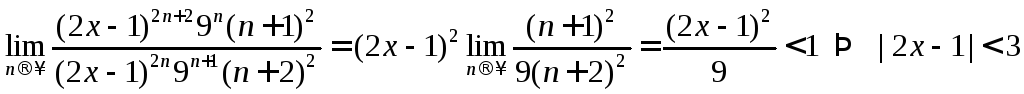
Решая это неравенство,
получим
![]() Исследуем сходимость на концах интервала:
Исследуем сходимость на концах интервала:
При
![]() получаем числовой ряд
получаем числовой ряд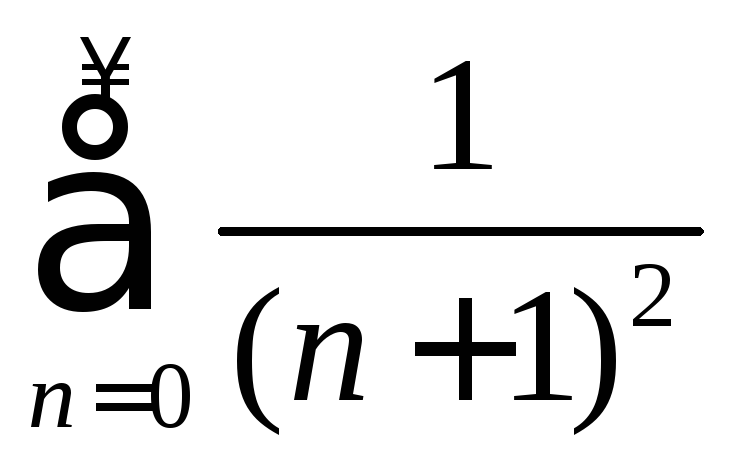 ,
который сходится как обобщенный
гармонический с
,
который сходится как обобщенный
гармонический с![]() .
.
При
![]() получаем такой же ряд.
получаем такой же ряд.
Окончательно,
областью сходимости является отрезок
![]()
