- •Интегральное исчисление Лекция № 25. Тема 1: Неопределённый интеграл
- •1.1. Первообразная и неопределённый интеграл
- •Лекция № 26
- •1.5. Интегрирование некоторых функций, содержащих квадратный трёхчлен
- •1.6. Интегрирование по частям
- •1.7. Многочлены и рациональные дроби
- •Лекция № 27
- •1.8. Интегрирование рациональных дробей
- •1.9. Интегрирование тригонометрических функций
- •Лекция № 28
- •1.10. Интегрирование некоторых иррациональных функций
- •1.11. Понятие о неберущихся интегралах
- •Лекция № 29. Тема 2 : Определённый интеграл
- •2.1. Задачи, приводящие к понятию определённого интеграла
- •2.2. Определение определённого интеграла
- •2.3. Основные свойства определённого интеграла
- •4. .
- •2.4. Интеграл как функция верхнего предела
- •Лекция № 30
- •2.7. Интегрирование по частям в определённом интеграле
- •Лекция № 31. Тема 3 : Приложения определённого интеграла
- •3.1. Площадь плоской фигуры
- •3.2. Длина дуги плоской кривой
- •3.3. Площадь поверхности тела вращения
- •3.4. Вычисление объёма тела по площадям поперечных сечений
- •Лекция № 32
- •3.5. Приложения определённого интеграла к некоторым задачам физики
- •Тема 4 : Несобственные интегралы
- •4.1. Несобственные интегралы первого рода (с бесконечными пределами)
- •4.2. Несобственные интегралы второго рода (от разрывных функций)
- •Функции нескольких переменных Лекция № 33. Тема 1 : Предел. Непрерывность. Частные производные
- •1.1. Определение функции нескольких переменных
- •1.2. Предел и непрерывность функции двух переменных
- •1.3. Частные производные функции двух переменных
- •1.4. Полный дифференциал функции двух переменных
- •1.5. Производная сложной функции
- •2.4. Производная по направлению
- •2.5. Градиент функции
- •Лекция № 35
- •2.6. Касательная и нормаль к поверхности
- •Тема 3* : Векторная функция скалярного аргумента
- •3.1. Векторная функция. Предел. Непрерывность
- •3.2. Производная векторной функции
- •. Лекция № 36. Тема 4 : Экстремум функции нескольких переменных
- •4.1. Необходимые условия экстремума
- •4.2. Достаточные условия экстремума
- •4.3. Нахождение наибольшего и наименьшего значений функции
- •Лекция № 37
- •4.4. Условный экстремум
- •4.5. Метод наименьших квадратов
- •Дифференциальные уравнения Лекция № 38. Тема 1 : Введение
- •1.1. Задачи, приводящие к дифференциальным уравнениям
- •1.2. Определение дифференциального уравнения
- •Тема 2: Дифференциальные уравнения первого порядка
- •2.1. Общие понятия. Теорема существования и единственности
- •2.2. Уравнения с разделяющимися переменными
- •Лекция № 39
- •2.3. Однородные уравнения
- •Лекция № 40. Тема 3 : ду высших порядков
- •3.1. Определение ду п-го порядка
- •3.2. Уравнения, допускающие понижение порядка
- •4.2. Теорема о структуре общего решения лоду-2
- •Лекция № 41
- •4.3. Лоду-2 с постоянными коэффициентами
- •4.4. Линейные неоднородные дифференциальные уравнения второго порядка
- •4.5. Метод вариации произвольных постоянных (метод Лагранжа)
- •Лекция № 42
- •4.6. Лнду-2 с постоянными коэффициентами со специальной правой частью
- •6.2. Решение нормальных систем ду методом исключений
Интегральное исчисление Лекция № 25. Тема 1: Неопределённый интеграл
1.1. Первообразная и неопределённый интеграл
Ранее для заданной
функции
![]() мы находили производную
мы находили производную![]() .
Теперь рассмотрим обратную задачу:
Известна производная
.
Теперь рассмотрим обратную задачу:
Известна производная![]() .
Требуется найти
.
Требуется найти![]() ,
которая называется первообразной.
,
которая называется первообразной.
С точки зрения механики – по скорости требуется восстановить движение материальной точки.
Определение 1.
Функция
![]() называется первообразной на некотором
промежутке
называется первообразной на некотором
промежутке
![]() для функции
для функции
![]() ,
если
,
если![]() для всехх
из этого промежутка.
для всехх
из этого промежутка.
Пример 1.
Если
![]() ,
то
,
то![]() получаем
получаем![]() ,
так как
,
так как![]() .
Кроме того, замечаем, что первообразными
будут являться также функции
.
Кроме того, замечаем, что первообразными
будут являться также функции![]() и т.д.
и т.д.
Таким образом, первообразные отличаются на константу.
Теорема.
Если
![]() и
и![]() первообразные на
первообразные на![]() ,
то
,
то![]() выполняется
выполняется![]() ,
где
,
где![]() .
.
Обозначим
![]() и применим к этой функции теорему
Лагранжа:
и применим к этой функции теорему
Лагранжа:![]() ,
так как
,
так как![]() ,
то
,
то![]() .
.![]()
Замечание 1. Если первообразную определить на некотором множестве, а не промежутке, то данная теорема, вообще говоря, неверна, что видно из примера:
Две функции
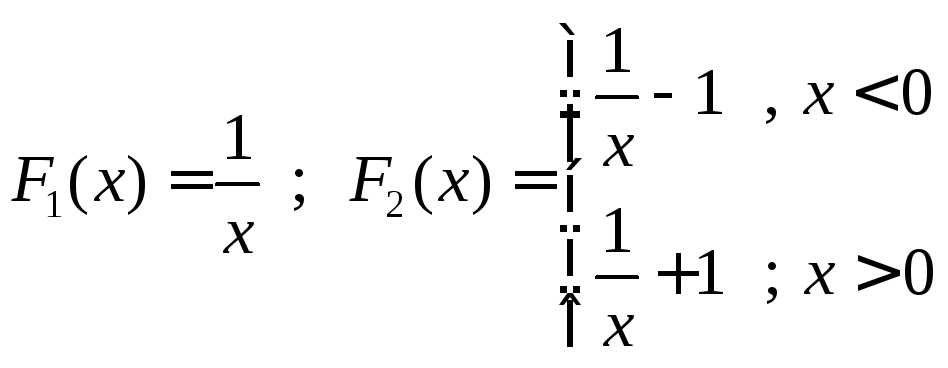 являются первообраз-ными для функции
являются первообраз-ными для функции .
Однако, их разность
.
Однако, их разность
![]()
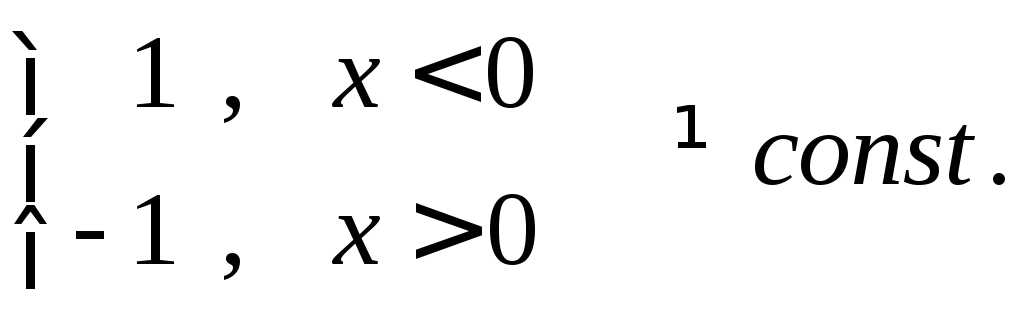
Определение 2.
Множество всех первообразных на некотором
проме-жутке называется неопределённым
интегралом от функции
![]() и обозна-чается
и обозна-чается
![]() .
.
Выражение
![]() называетсяподынтегральным.
Операция нахождения неопределённого
интеграла называется интегрированием
функции
называетсяподынтегральным.
Операция нахождения неопределённого
интеграла называется интегрированием
функции
![]() .
.
С геометрической
точки зрения неопределённый интеграл
представляет собой множество кривых
![]() ,
получаемых путём сдвига одной из них
параллельно самой себе вдоль осиОу.
,
получаемых путём сдвига одной из них
параллельно самой себе вдоль осиОу.
1.2. Основные свойства неопределённого интеграла
1.
![]() .
.
Действительно,
![]() .
.
2.
![]() .
.
Действительно,
![]() .
.
3.
Свойство линейности:
![]() ,
где
,
где![]() .
.
Продифференцируем обе части этого равенства.
Для левой части
получаем
![]() .
.
Для правой:
![]() .
.
4.
 ,
где
,
где![]() .
.
Доказывается аналогично дифференцированием.
1.3. Таблица неопределённых интегралов
Непосредственным дифференцированием можно проверить следующие формулы:
1.
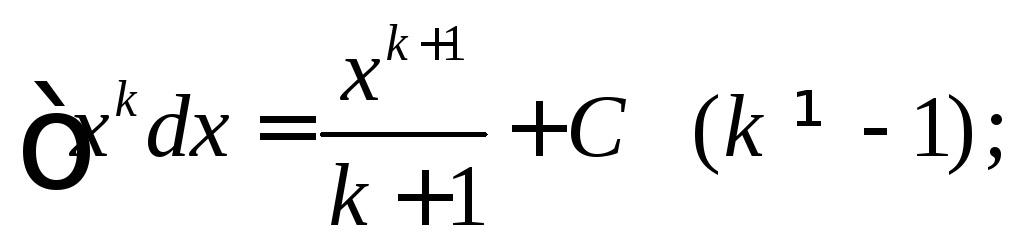 4.
4.![]()
2.
![]() 5.
5.![]()
3.
![]() 6.
6.![]()
7.
![]() 11.
11.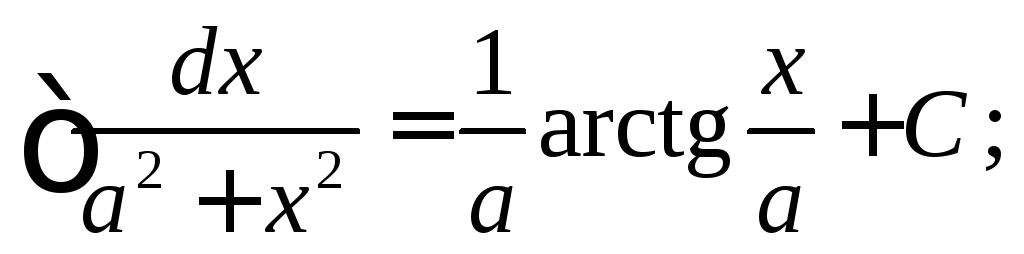
8.
![]() 12.
12.![]()
9.
 13.
13.![]()
10.
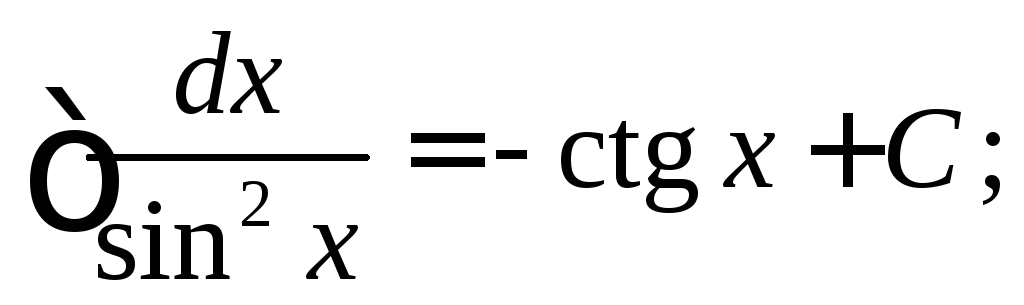 14.
14.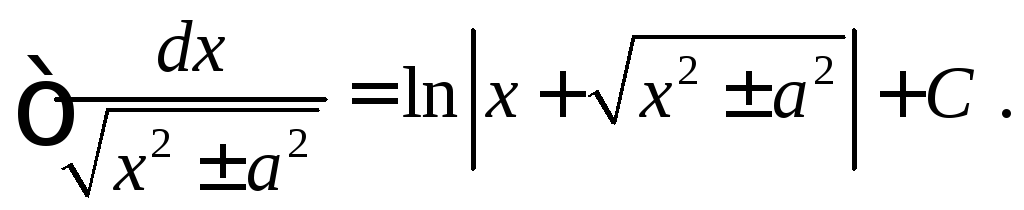
Замечание 2.
Используя свойство 4,
таблицу неопределённых интегралов
можно расширить. Например,
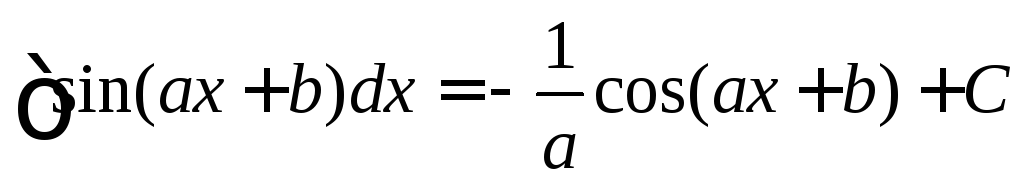 .
.
С помощью этой таблицы можно находить некоторые интегралы.
Пример 2.
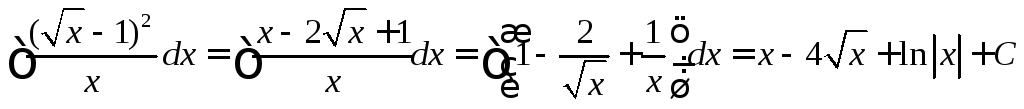 .
.
Пример 3.
 .
.
1.4. Интегрирование методом замены переменной (способ подстановки)
Пусть функция
![]() является дифференцируемой и имеет
обратную функцию
является дифференцируемой и имеет
обратную функцию![]() .
Тогда имеет место формула, которая
проверяется дифференцированием:
.
Тогда имеет место формула, которая
проверяется дифференцированием:
![]() .
(1)
.
(1)
Действительно,
продифференцируем левую часть:
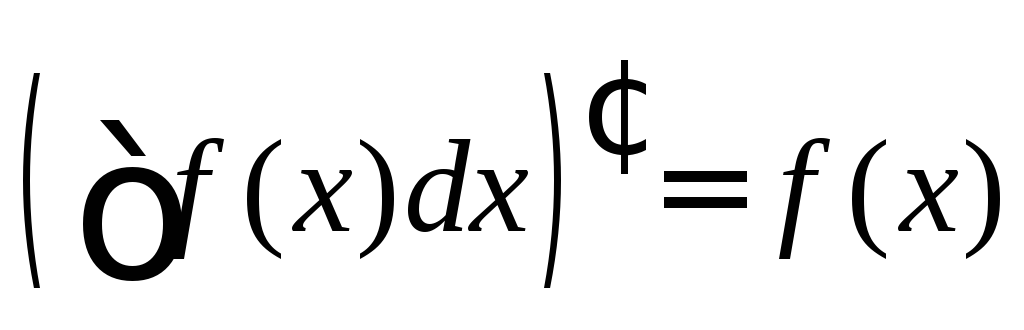 ,
,
Затем продифференцируем правую часть
![]() = (по правилу
дифференцирования сложной функции)
=
= (по правилу
дифференцирования сложной функции)
=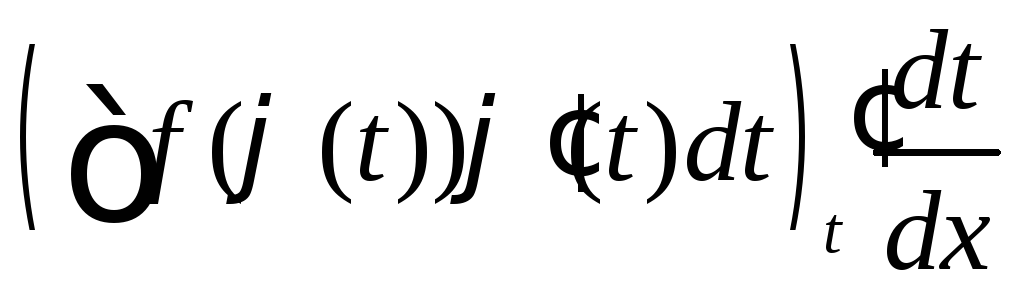 = (по правилу дифференцирования обратной
функции) =
= (по правилу дифференцирования обратной
функции) =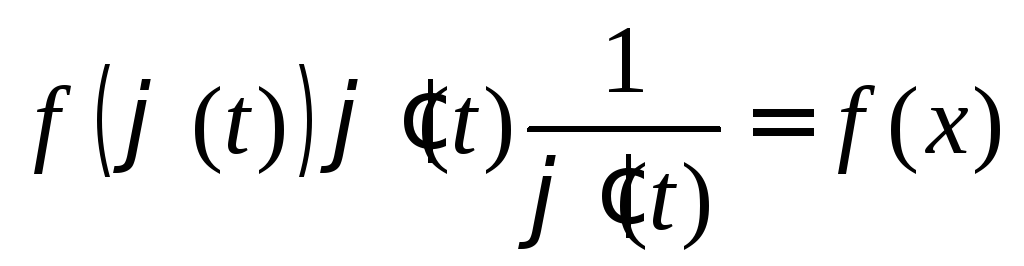 .
.
Замечание 3.
Функцию
![]() следует выбирать так, чтобы интеграл
в правой части формулы (1) можно было
найти.
следует выбирать так, чтобы интеграл
в правой части формулы (1) можно было
найти.
Замечание 4. В практике нахождений интегралов константу С не пишут для каждого интеграла, так как они в конечном итоге будут входить в окончательный ответ, содержащий произвольную константу.
Замечание 5.Часто
более целесообразно применять замену
переменной в виде
![]() .
Это в том случае, когда интеграл можно
представить в виде
.
Это в том случае, когда интеграл можно
представить в виде![]() .
Например,
.
Например,
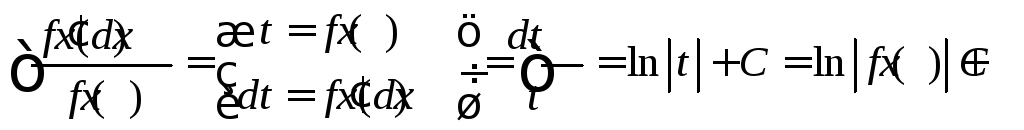 .
.
Пример 4.
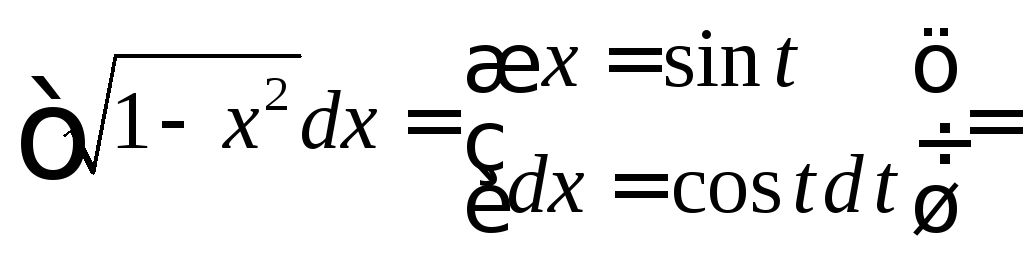



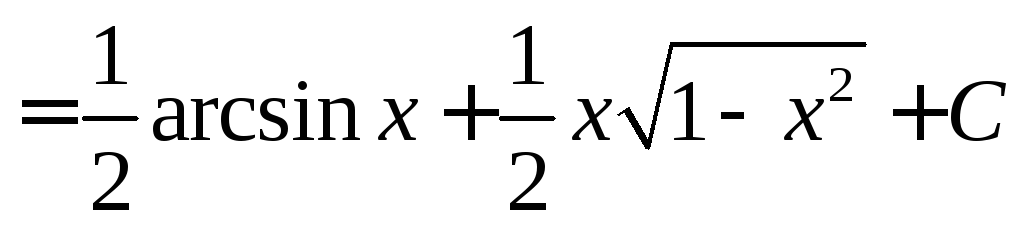 .
.
Пример 5.
 .
.
Пример 6.
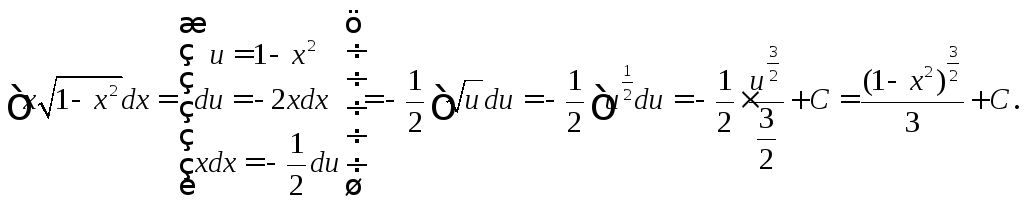
Пример 7. Найдите ошибку:
На основании свойства 4 имеем
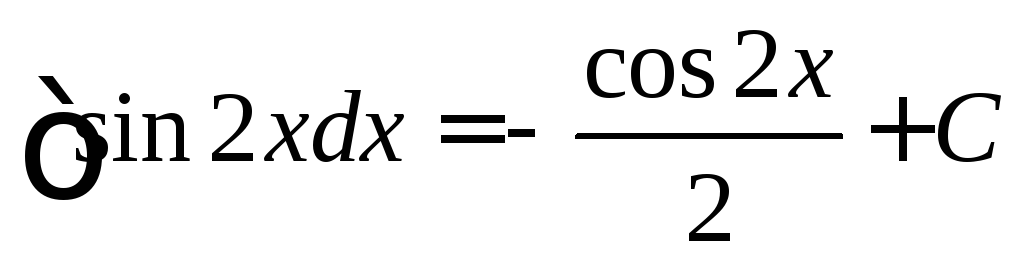 .
.
С другой стороны

Отсюда следует