Тема 2: Дифференциальные уравнения первого порядка

2.1. Общие понятия. Теорема существования и единственности

Общий вид дифференциального уравнения первого порядка (ДУ-1)

. (2)

Если уравнение можно разрешить относительно производной, то

, (3)

где функция определена в некоторой областиD.

Для примера рассмотрим уравнение Нетрудно убедится в том, что его решением является функция, гдеС - произвольная постоянная. И на любых других примерах можно убедится в том, что любое решение ДУ-1 есть бесконечное множество функций, которые определяются формулой, содержащей одну произвольную постоянную С,т.е. имеют вид

или . (4)

Определение 4. Общим решением или общим интегралом уравнения (2) или (3) называется функция (4) удовлетворяющая условиям:

1. Обращает в тождество уравнение при любых значениях С;

2. Для любой точки можно найти такое значение постояннойдля которогоили.

Давая произвольной постоянной С различные числовые значения, из общего решения получим так называемые частные решения.

Для того, чтобы из общего решения выделить конкретное частное решение, необходимо задать начальное условие, т.е. условие вида

или . (5)

В этом случае задача о нахождении частного решения называется задачей Коши.

Пример 1. Решить задачу Коши:

Как было показано, общее решение имеет вид . Определим константуС, исходя из начального условия

решение задачи Коши.

Теорема Коши. Если в дифференциальном уравнении функциянепрерывна в некоторой областиD, содержащей точку , то существует решениеэтого уравнения, удовлетво-ряющее начальному условию. Если, кроме этого, в этой области непрерывна производная, то решение уравнения единственно.

Пример 2. Найти область единственности решения ДУ

.

Здесь 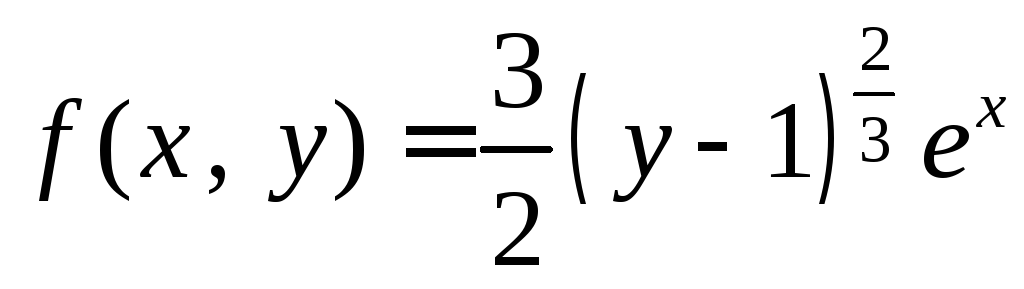. Тогда

и при возможно нарушение единственности решения. Во всех остальных точках решение единственное.

2.2. Уравнения с разделяющимися переменными

Рассмотрим ДУ-1 (3). Если , то уравнение (3) можно пред-ставить в виде

.

Если к тому же

,

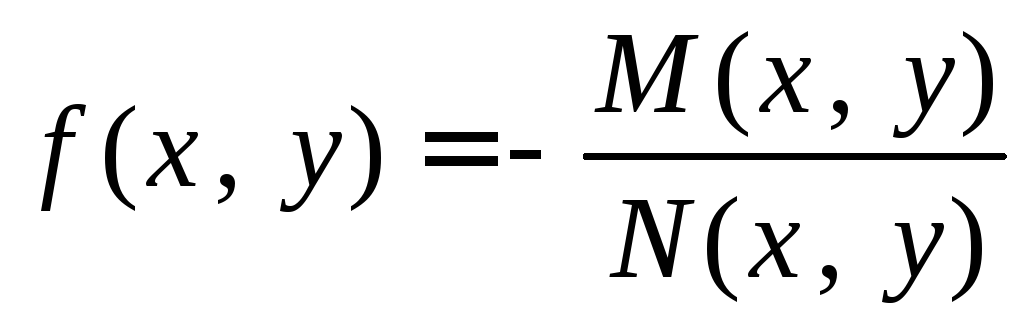то

. (6)

Пусть в уравнении (6) выполняются условия:

,

тогда оно примет вид

. (7)

Определение 5. Уравнение (7) называется уравнением с разделяющи-мися переменными.

Разделим уравнение (7) на произведение , тогда получим

(8)

Интегрируя уравнение (8), получим его общий интеграл

(9)

Замечание 2. Особого внимания требуют точки, где обращаются в нуль функции и. Пусть, например,. Тогда уравнение (7) наряду с решением (9) имеет и решение. Аналогично, если, тоявляется решением уравнения (7).

Пример 3.Найтиобщеерешениеуравнения .

Преобразуем уравнение:

или

,

при этом . Интегрируя уравнение, получим

или

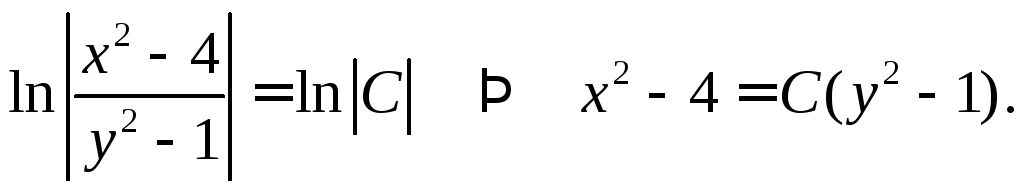
К этому решению нужно добавить решение вида , а решение видавходит в общее решение при. Окончательно, имеем

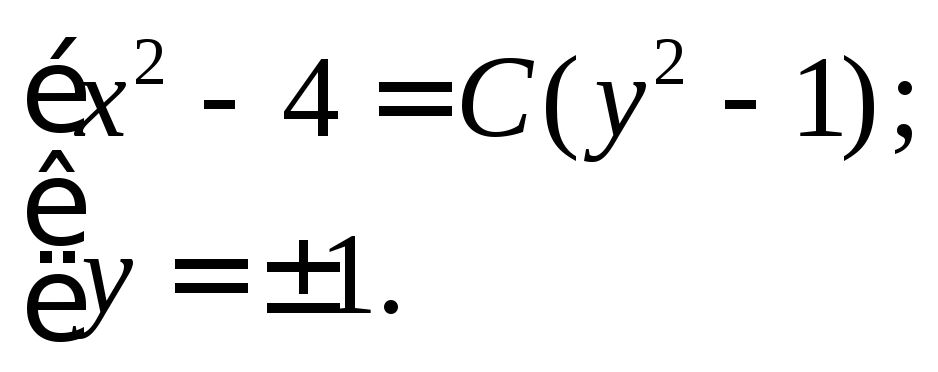
Пример 4. Решить задачу о радиоактивном распаде вещества:

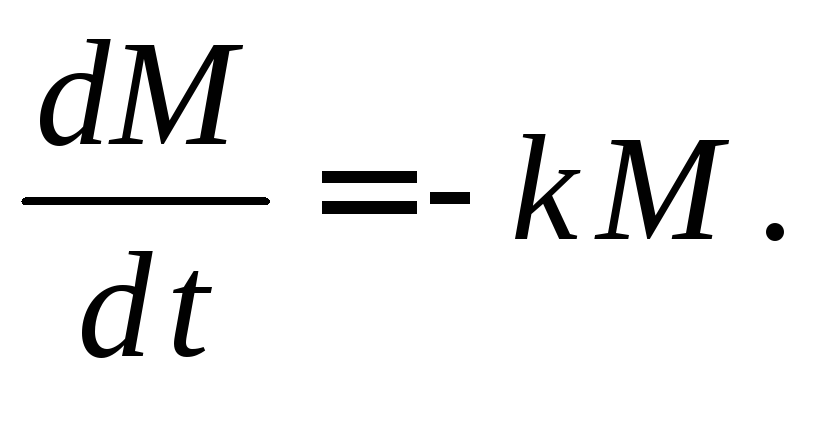
Разделим переменные:

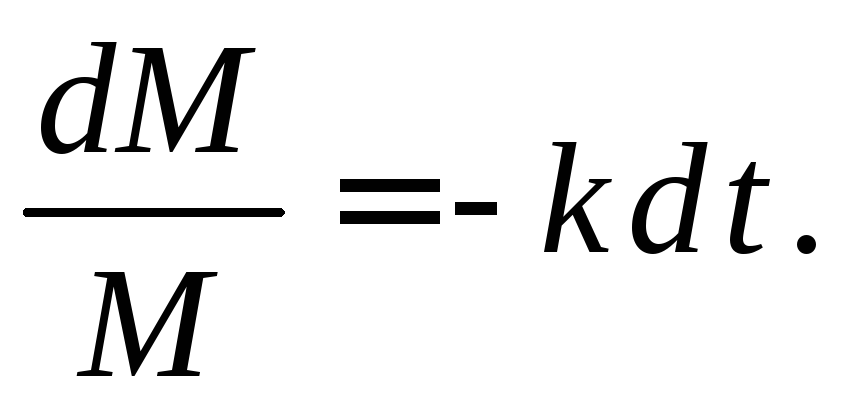
Интегрируя, получим

или .

Если известна начальная масса M₀ при , тогда

и .

Определим коэффициент k из наблюдений. Пусть за время t₁ масса вещества стала равной M₁. Тогда

Таким образом, получили конкретный вид закона изменения заданной массы радиоактивного вещества в зависимости от времени.