- •Интегральное исчисление Лекция № 25. Тема 1: Неопределённый интеграл
- •1.1. Первообразная и неопределённый интеграл
- •Лекция № 26
- •1.5. Интегрирование некоторых функций, содержащих квадратный трёхчлен
- •1.6. Интегрирование по частям
- •1.7. Многочлены и рациональные дроби
- •Лекция № 27
- •1.8. Интегрирование рациональных дробей
- •1.9. Интегрирование тригонометрических функций
- •Лекция № 28
- •1.10. Интегрирование некоторых иррациональных функций
- •1.11. Понятие о неберущихся интегралах
- •Лекция № 29. Тема 2 : Определённый интеграл
- •2.1. Задачи, приводящие к понятию определённого интеграла
- •2.2. Определение определённого интеграла
- •2.3. Основные свойства определённого интеграла
- •4. .
- •2.4. Интеграл как функция верхнего предела
- •Лекция № 30
- •2.7. Интегрирование по частям в определённом интеграле
- •Лекция № 31. Тема 3 : Приложения определённого интеграла
- •3.1. Площадь плоской фигуры
- •3.2. Длина дуги плоской кривой
- •3.3. Площадь поверхности тела вращения
- •3.4. Вычисление объёма тела по площадям поперечных сечений
- •Лекция № 32
- •3.5. Приложения определённого интеграла к некоторым задачам физики
- •Тема 4 : Несобственные интегралы
- •4.1. Несобственные интегралы первого рода (с бесконечными пределами)
- •4.2. Несобственные интегралы второго рода (от разрывных функций)
- •Функции нескольких переменных Лекция № 33. Тема 1 : Предел. Непрерывность. Частные производные
- •1.1. Определение функции нескольких переменных
- •1.2. Предел и непрерывность функции двух переменных
- •1.3. Частные производные функции двух переменных
- •1.4. Полный дифференциал функции двух переменных
- •1.5. Производная сложной функции
- •2.4. Производная по направлению
- •2.5. Градиент функции
- •Лекция № 35
- •2.6. Касательная и нормаль к поверхности
- •Тема 3* : Векторная функция скалярного аргумента
- •3.1. Векторная функция. Предел. Непрерывность
- •3.2. Производная векторной функции
- •. Лекция № 36. Тема 4 : Экстремум функции нескольких переменных
- •4.1. Необходимые условия экстремума
- •4.2. Достаточные условия экстремума
- •4.3. Нахождение наибольшего и наименьшего значений функции
- •Лекция № 37
- •4.4. Условный экстремум
- •4.5. Метод наименьших квадратов
- •Дифференциальные уравнения Лекция № 38. Тема 1 : Введение
- •1.1. Задачи, приводящие к дифференциальным уравнениям
- •1.2. Определение дифференциального уравнения
- •Тема 2: Дифференциальные уравнения первого порядка
- •2.1. Общие понятия. Теорема существования и единственности
- •2.2. Уравнения с разделяющимися переменными
- •Лекция № 39
- •2.3. Однородные уравнения
- •Лекция № 40. Тема 3 : ду высших порядков
- •3.1. Определение ду п-го порядка
- •3.2. Уравнения, допускающие понижение порядка
- •4.2. Теорема о структуре общего решения лоду-2
- •Лекция № 41
- •4.3. Лоду-2 с постоянными коэффициентами
- •4.4. Линейные неоднородные дифференциальные уравнения второго порядка
- •4.5. Метод вариации произвольных постоянных (метод Лагранжа)
- •Лекция № 42
- •4.6. Лнду-2 с постоянными коэффициентами со специальной правой частью
- •6.2. Решение нормальных систем ду методом исключений
Лекция № 27
1.8. Интегрирование рациональных дробей
На основании рассмотренной в предыдущей лекции теоремы преобра-зуется подынтегральная рациональная функция и нахождение интеграла сводится к интегрированию простейших дробей. Коэффициенты в числи-телях этих дробей вычисляются методом неопределённых коэффициентов.
Пример 1.
![]() .
.
Преобразуем подынтегральную функцию, представив её как сумму простейших дробей
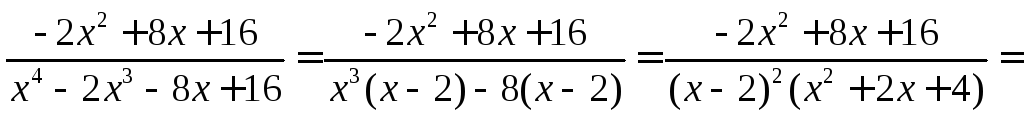
 .
.
Определим
коэффициенты
![]() .
Для этого приведём дроби в правой части
равенства к общему знаменателя и
приравняем числители дробей в правой
и левой частей полученного равенства
.
Для этого приведём дроби в правой части
равенства к общему знаменателя и
приравняем числители дробей в правой
и левой частей полученного равенства
![]() .
.
Приравнивая коэффициенты при одинаковых степенях х (метод неопределённых коэффициентов), приходим к системе

Упростим систему,
учитывая, что
![]() ,
,
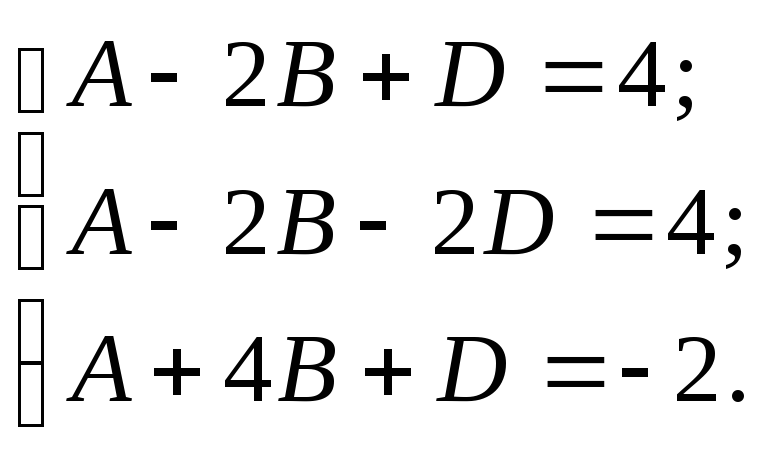
Из первых двух
уравнений получаем
![]() ,
из первого и третьего
,
из первого и третьего
![]() и
и![]() ,
,![]() .
.
Тогда наш интеграл приводится к нахождению интегралов

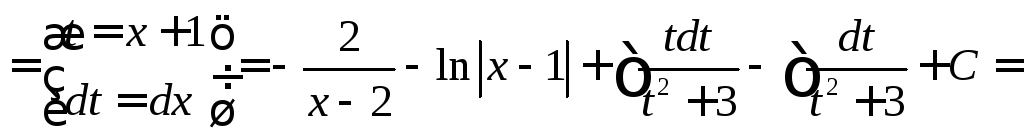
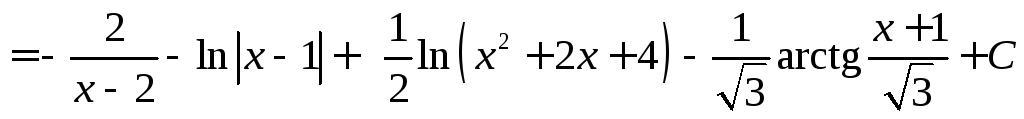 .
.
1.9. Интегрирование тригонометрических функций
1.9.1. Интегралы
вида
![]() ,
гдеR
рациональная функция,
,
гдеR
рациональная функция,
приводятся к
интегралу от рациональной функции путём
замены
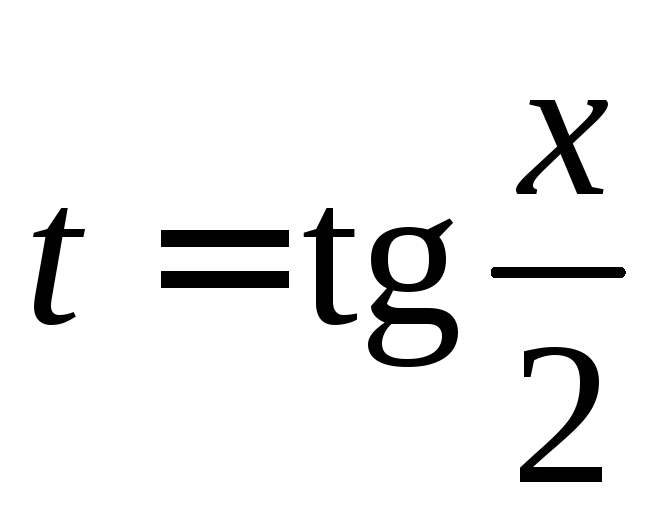 ,
которая называетсяуниверсальной
тригонометрической
подстановкой. Это достигается тем, что
,
которая называетсяуниверсальной
тригонометрической
подстановкой. Это достигается тем, что
![]() и
и![]() выражаются через
выражаются через![]() рационально:
рационально:
 (1)
(1)
Пример 2.
![]() (воспользуемся
формулами (1)) =
(воспользуемся
формулами (1)) =
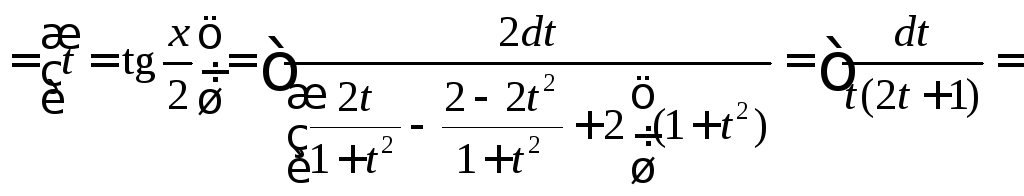
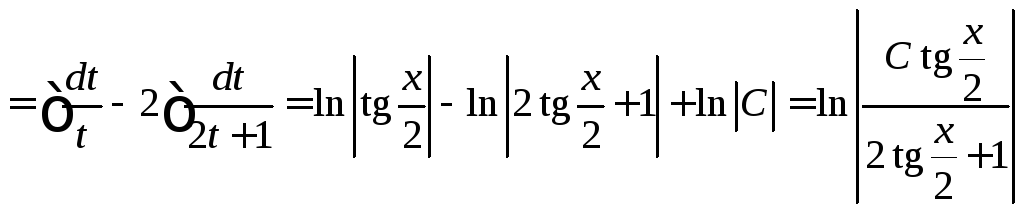 .
.
Замечание.
Использование такой подстановки часто
приводит к громоздким выражениям. Эта
подстановка, как правило, эффективна,
если
![]() и
и![]() входят в дробное выражение в первой
степени.
входят в дробное выражение в первой
степени.
1.9.2. Интегралы вида
![]() с помощью подстановок:
с помощью подстановок:![]() соответственно приводятся к интегралам
от рациональной функции.
соответственно приводятся к интегралам
от рациональной функции.
Пример 3.

 .
.
1.9.3. Интегралы
вида
![]() .
.
В этом случае
применяется замена
![]() ,
так как
,
так как![]() и
и![]() выражаются через
выражаются через![]() рационально:
рационально:![]() ,
или используются тригонометрические
формулы понижения степени.
,
или используются тригонометрические
формулы понижения степени.
Пример 4.
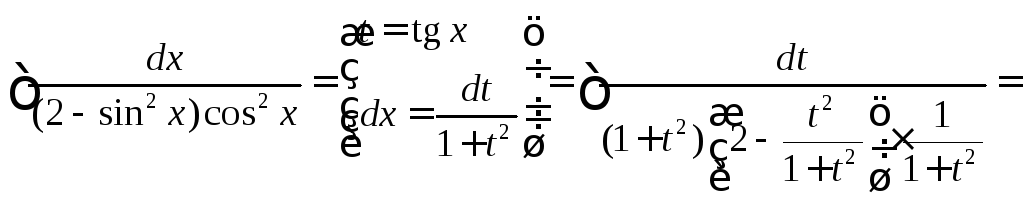
 .
.
1.9.4. Интегралы вида
![]() ,
где среди показателейт
и п
по крайней мере одно нечетное.
,
где среди показателейт
и п
по крайней мере одно нечетное.
В этом случае за
новую переменную
![]() принимается та функция, которая содержит
чётную степень, либо любая, если все
функции в нечётных степенях.
принимается та функция, которая содержит
чётную степень, либо любая, если все
функции в нечётных степенях.
Пример 5.
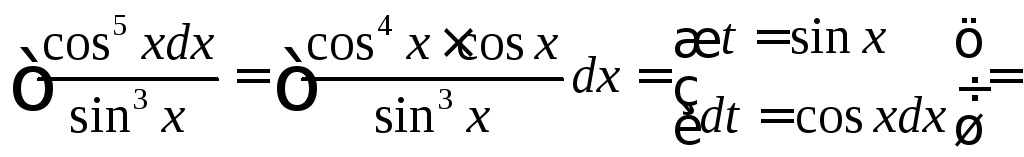
 .
.
1.9.5. Интегралы
вида![]() .
.
Эти интегралы находятся с использованием формул:
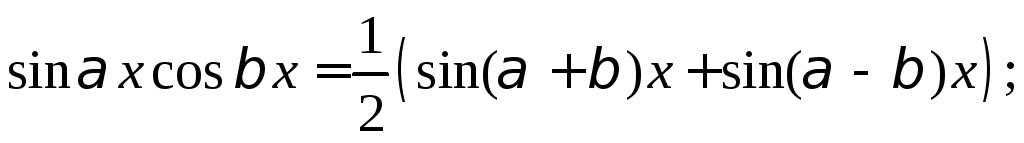
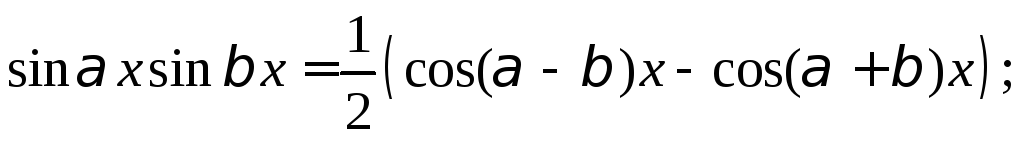

Пример 6.
![]() .
.
Лекция № 28
1.10. Интегрирование некоторых иррациональных функций
Рассмотрим только некоторые частные случаи, когда интеграл от иррациональной функции выражается через элементарные функции.
1.10.1. Интегралы
вида
![]() .
.
Если
![]() ,
то подстановка имеет вид
,
то подстановка имеет вид![]() и тогда
и тогда![]() .
После чего интегрирование сводится к
интегрированию рациональных дробей.
.
После чего интегрирование сводится к
интегрированию рациональных дробей.
Пример 1.

![]()
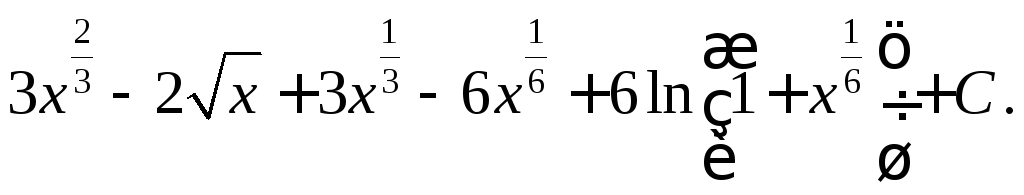
Замечание 1.
Если выражение под знаком радикала
линейное, т.е. имеет вид
![]() ,
то из свойства4
следует, что мы вправе применить тот
же подход.
,
то из свойства4
следует, что мы вправе применить тот
же подход.
Пример 2.
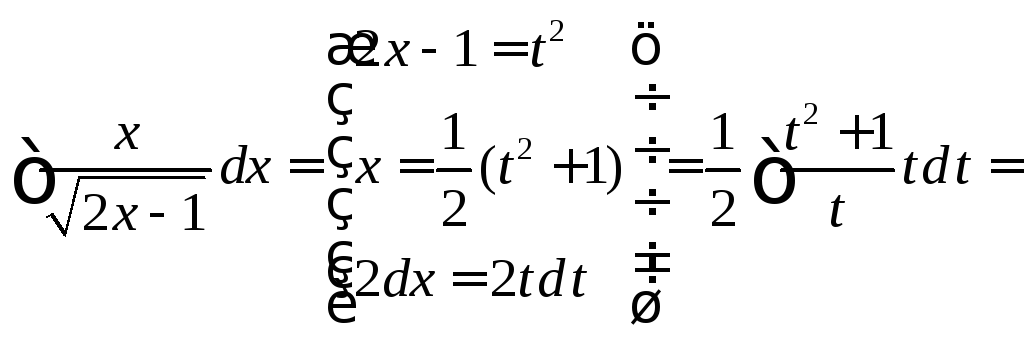
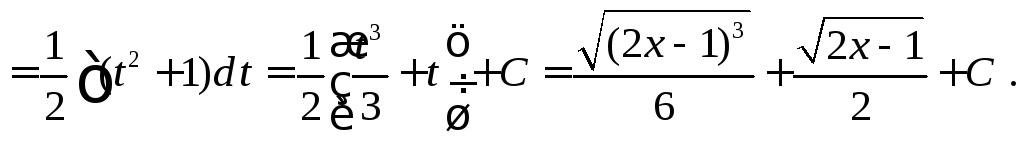
1.10.2. Интегралы
вида
 .
.
Аналогично, если
![]() ,
то подстановка
,
то подстановка![]() также приводит к интегрированию
рациональных дробей.
также приводит к интегрированию
рациональных дробей.
Пример 3.
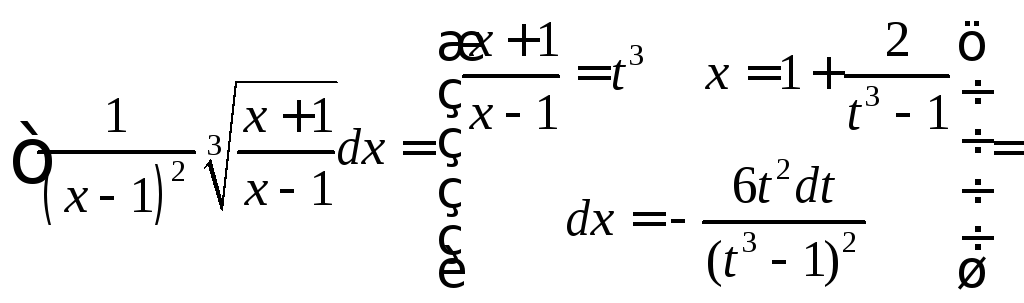
 .
.
1.10.3*. Интегралы
вида
![]() .
.
Преобразуем
выражение под знаком радикала. Если за
знак радикала вынести
![]() ,
то получим
,
то получим![]() .
Выполнив замену
.
Выполнив замену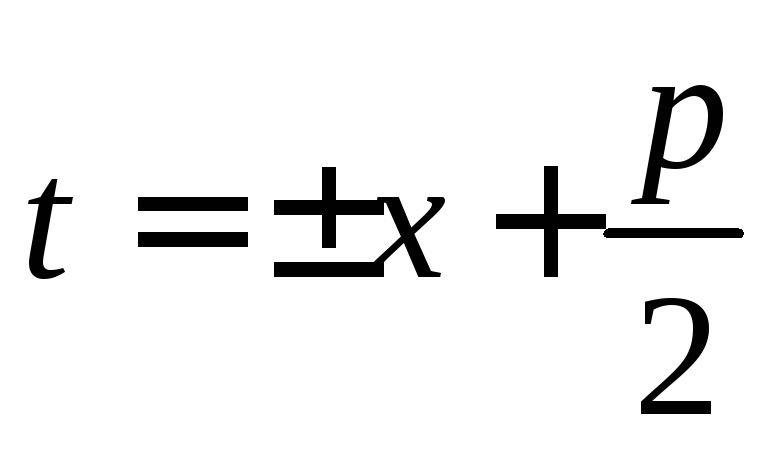 ,
приходим к трём случаям:
,
приходим к трём случаям:
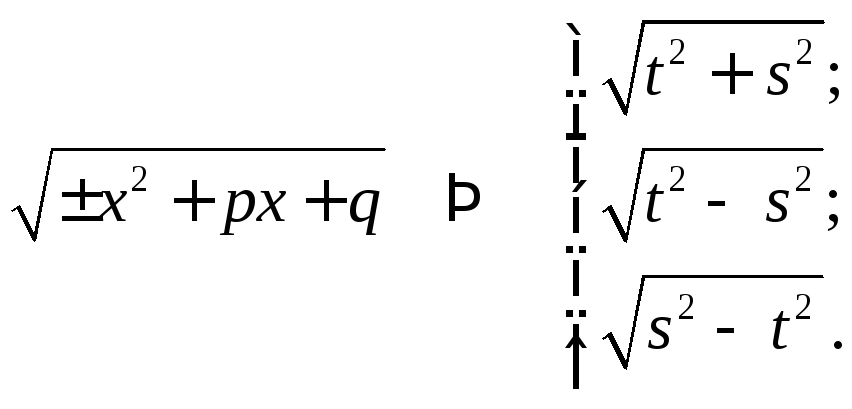
Рассмотрим каждый
из этих случаев отдельно. Естественно,
случай
![]() не рассматривается.
не рассматривается.
1. Интегралы вида
![]() .
.
Заменой
![]() такие интегралы приводятся к интегралам
от рациональной функции.
такие интегралы приводятся к интегралам
от рациональной функции.
Пример 3.
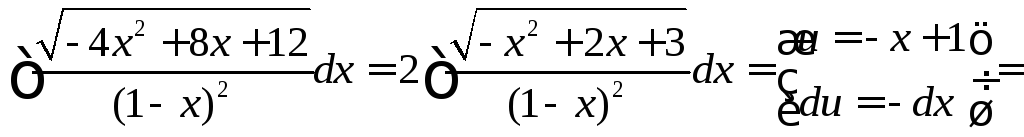
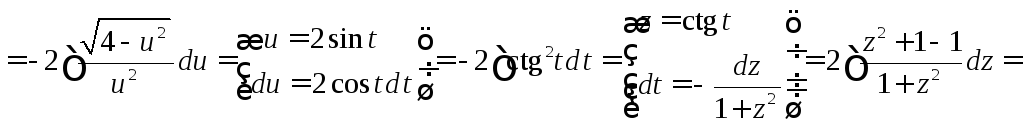
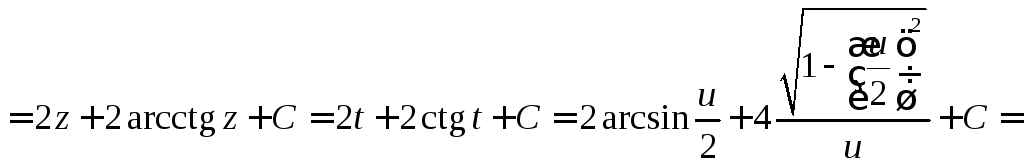
![]() .
.
2. Интегралы вида
![]()
В этом случае
используется замена
![]() .
.
Пример 4.
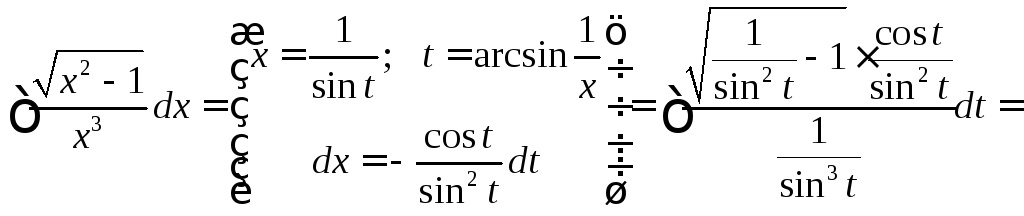
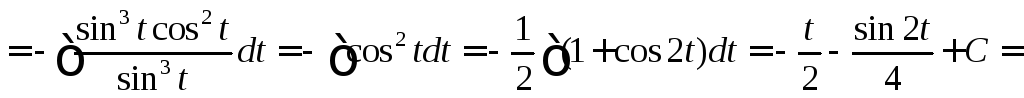
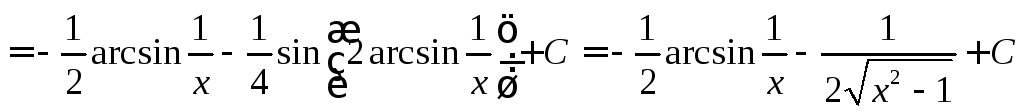 .
.
3. Интегралы вида
![]() .
.
Рационализация
подынтегрального выражения достигается
заменой
![]() .
.
Пример 5.