4.2. Несобственные интегралы второго рода (от разрывных функций)

Если функция наимеет конечное число точек разрыва первого рода, то вычисление интеграла от такой функции трудности не представляет. Например, если точка разрыва первого рода, тогда

Если же функция имеет бесконечный разрыв, то в этом случае интеграл называется несобственным второго рода. Тогда, если точка разрыва второго рода, то интеграл определяется следующим образом

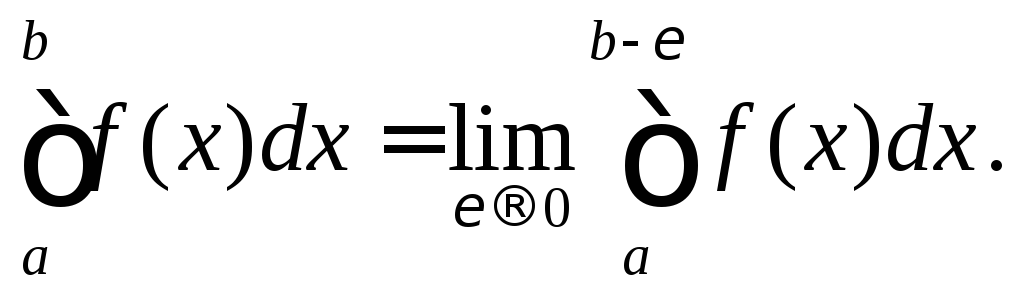
Аналогично определяются несобственные интегралы от функций с разрывами в точках и:

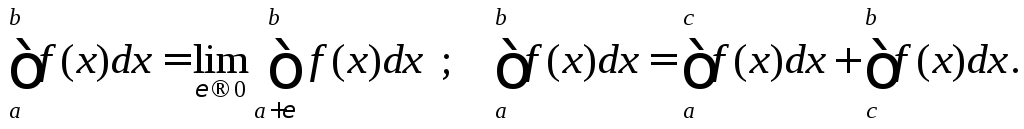
Если для несобственного интеграла от разрывной функции в точке известна первообразная, то его сходимость зависит от существования значения.

Пример 4. Исследовать сходимость .

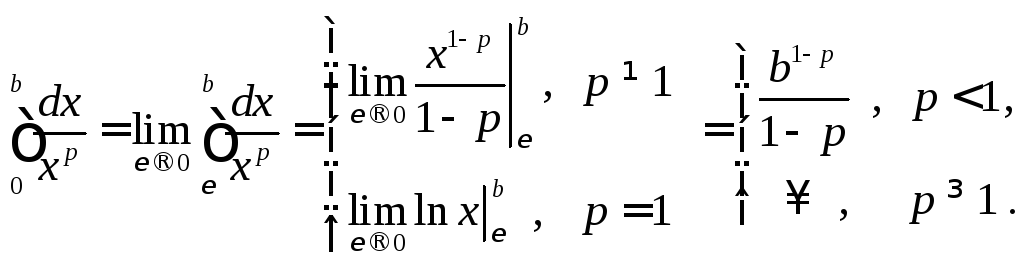
Таким образом, интеграл сходится, если степень и расходится, если.

Если же первообразная функции не известна, то для исследования сходимости, как и для несобственных интегралов первого рода, исполь-зуются аналогичные признаки сравнения.

Пример 5. Исследовать на сходимость интеграл и, если он сходится, вычислить его.

Замечаем, что в точке подынтегральная функция имеет разрыв второго рода, а интеграл запишем в виде

.

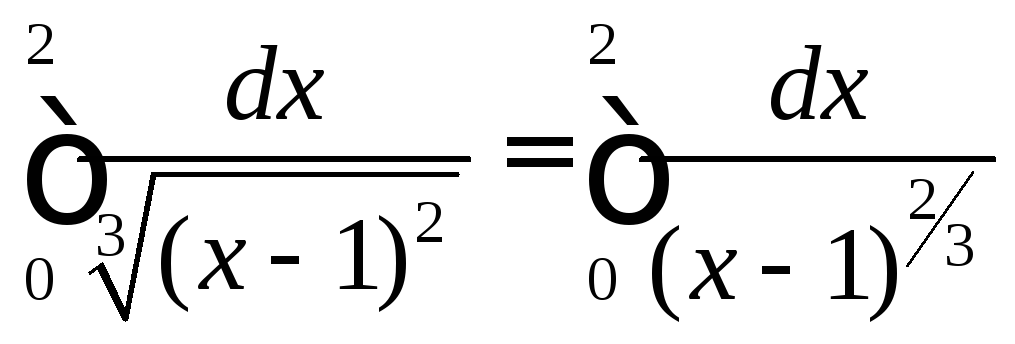Сравним подынтегральную функцию с эталонной функцией .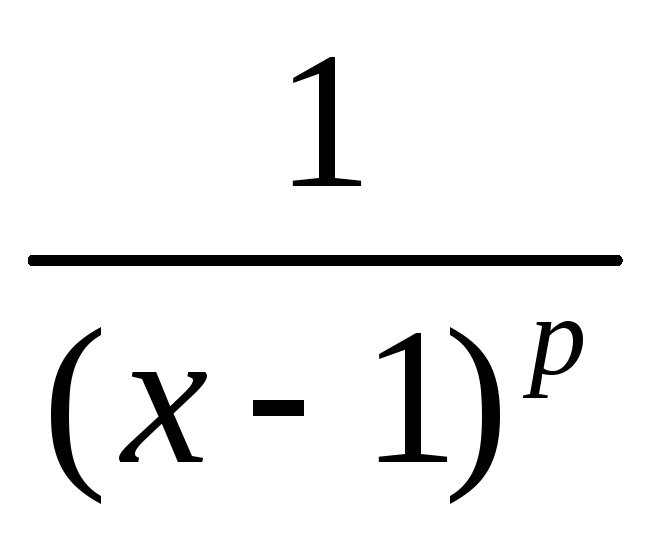

Тогда показатель р степени у подынтегральной функции равен , следовательно интеграл сходится. Вычислим его

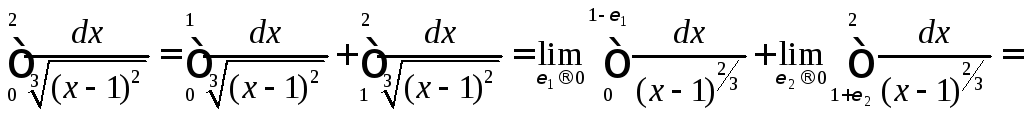
Функции нескольких переменных Лекция № 33. Тема 1 : Предел. Непрерывность. Частные производные

1.1. Определение функции нескольких переменных

Остановимся, в основном, на случае функции двух переменных. Определения и полученные результаты легко распространить и на случай большего числа переменных.

Рассмотрим плоскость Оху  множество всех точек .

Определение 1. Множество всех точек , координаты которых удовлетворяют неравенству, называетсяокрест-ностью точки и обозначается.

Определение 2. Областью D называется множество точек, обладающих свойствами:

1. Любая точка принадлежит ей и вместе с некоторой- окрестностью (свойство открытости);

2. Любые точки иможно соединить непрерывной линией, целиком принадлежащейD (свойство связности).

Линия, ограничивающая данную область, называетсяграницей. Если к области отнести и точки границы, то такая область называется замкнутой.

D

М₁ М₂

Определение 3. Если каждой паре значений двух независимых переменных из некоторой областиD соответствует по некоторому правилу или закону определённое значение величины z, то z называется функцией двух переменных в области D, и пишут .

Аналогично, как и для функции одной переменной определяется многозначная функция нескольких переменных.

Пример 1. Закон Ома:  функция двух переменных.

Пример 2. Работа постоянной силы на прямолинейном перемещении:  функция трёх переменных.

Определение 4. Множество значений , при которых определена, называетсяобластью определения функции.

Пример 3. Найти область определения функций:

1. , т.е. областью определения данной функции является круг.

2. , т.е. область определения первая и третья координатные четверти без координатных осей.

Геометрически функцию двух переменных можно представить как поверхность, уравнение которой . Например, уравнение функциигеометрически представляет параболоид.