3.2. Производная векторной функции

Дадим приращение аргументу t. В результате векторная функция получит приращение

Рассмотрим отношение . Если функцииявляются дифференцируемыми, то

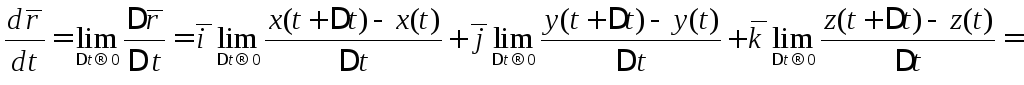
. (2)

Формула (2) определяет производную векторной функции скалярного аргумента. Модуль этого вектора равен

.

Выясним геометрический смысл производной.

М

М₁

О

Из рисунка видно, что при , т.е. производная имеет направлениекасательной. Нормалей к пространственной кривой в данной точке можно провести бесконечное множество – все они лежат в плоскости, которая называется нормальной плоскостью. Исходя из геометрического смысла производной, получаем уравнение касательной

и уравнение нормальной плоскости

.

Замечание 3. Из определения производной следует, что правила её нахождения такие же, как идля скалярной функции одного переменного.

Аналогично, как и для плоской линии, вводится понятие её кривизны.

Формула для вычисления кривизны пространственной линии имеет вид

.

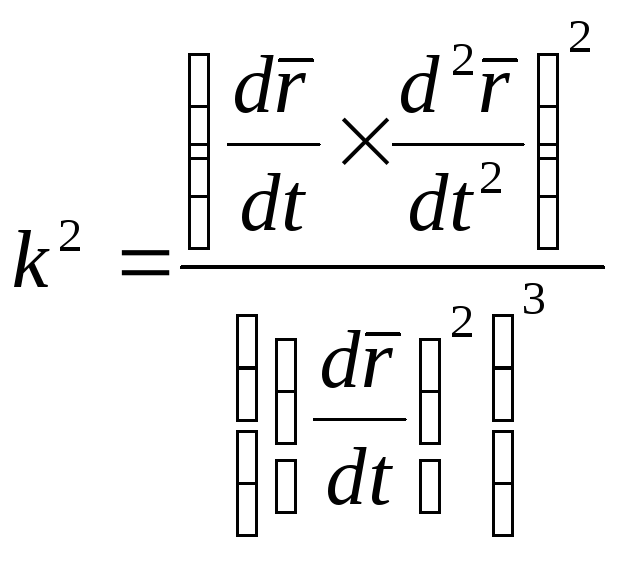Пример 2. Показать, что если то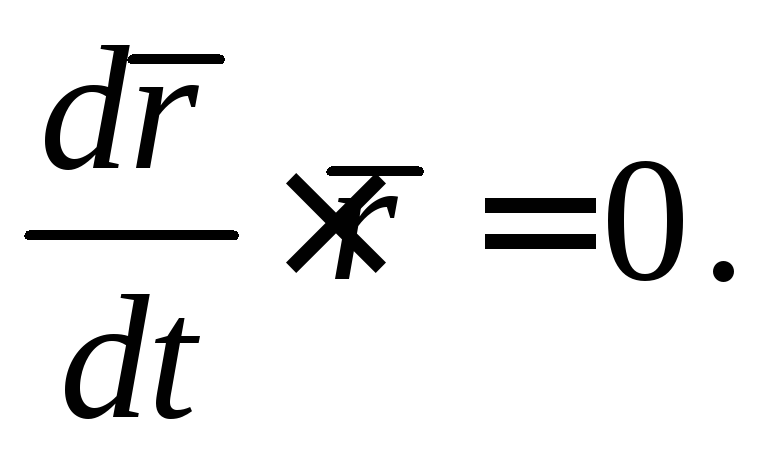

Действительно, так как то, дифференцируя, получаем, что и требовалось доказать.

Пример 3. Составить уравнение касательной, нормальной плоскости и вычислить кривизну винтовой линии в точке .

Вычислим значения функций и их производных в соответствующей точке:

Составим уравнение касательной

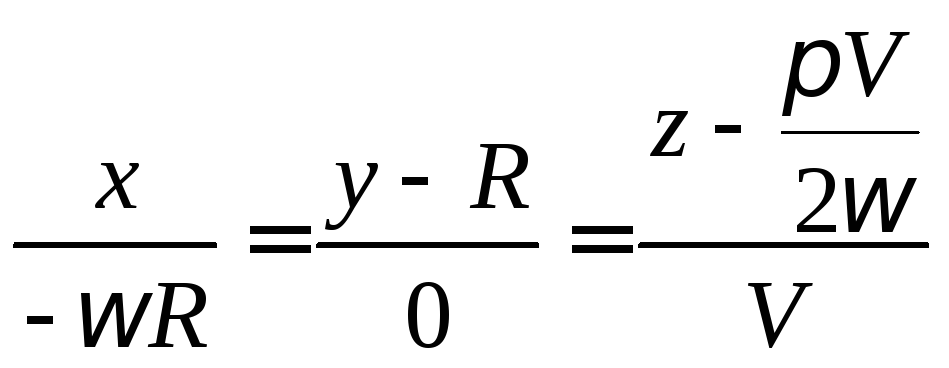
и нормальной плоскости

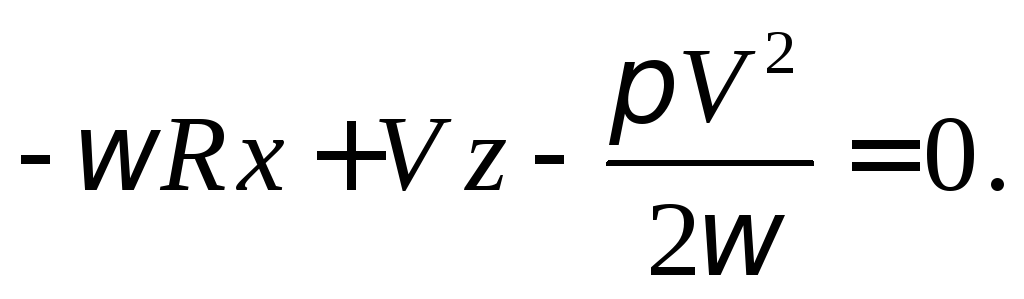
Для вычисления кривизны найдём векторное произведение векторов и

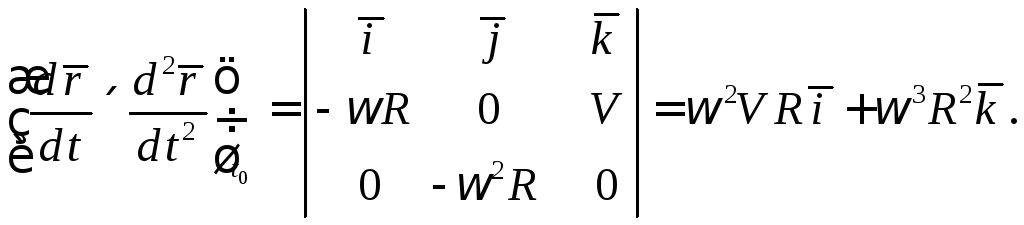
Тогда

. Лекция № 36. Тема 4 : Экстремум функции нескольких переменных

4.1. Необходимые условия экстремума

Определение 1. Функция имеет максимум (минимум) в точке, если для любой точкивыполняется неравенство. Максимум и минимум называются экстремумами функции.

Возьмем точку , дадим в ее окрестности приращения аргументам , тогда приращение функции

и, если, то точка- точка максимума, если точка минимума. z

Пример 1. Рассмотрим функцию

и точку (см. рис.).

В этой точке имеем

точка минимума. O y

x

Теорема (необходимые условия экстремума). Если функция достигает экстремума в точке, то в этой точке частные производныеиравны нулю, или не существуют.

Дадим переменной у определённое значение у₀. Тогда будет функцией одного переменногох. При значении она имеет экстремум, поэтому частная производная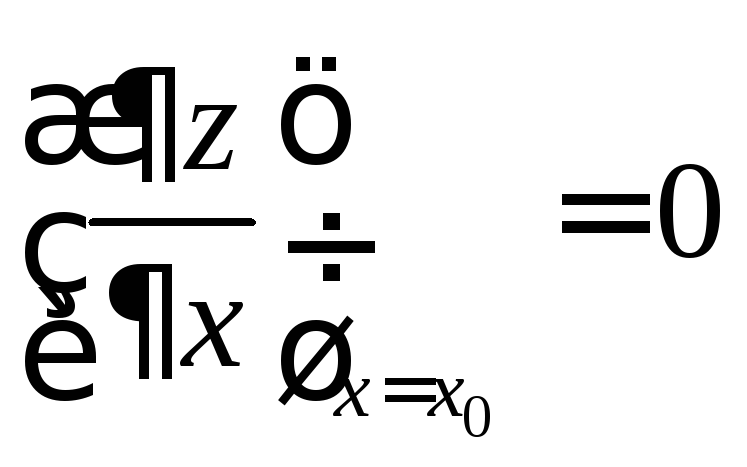, либо не существует.

Аналогично доказывается и для частной производной .

Это условие не является достаточным, что видно из примера.

Пример 2. Рассмотрим функцию .

Тогда

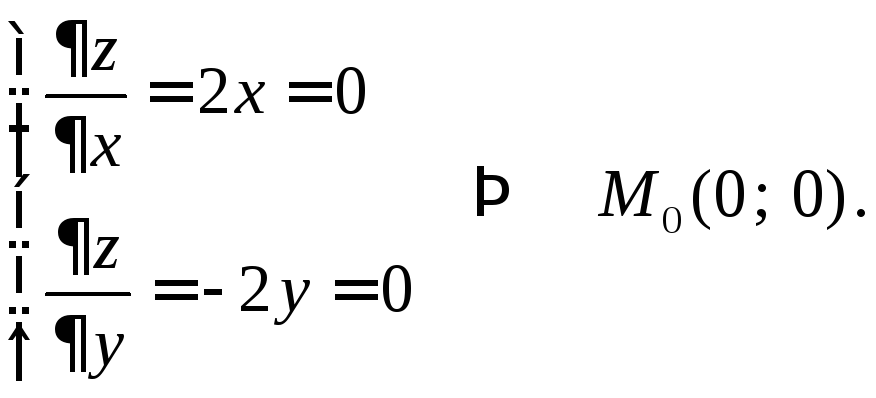
В этой точке полное приращение функции , откуда следует, что в её окрестностипринимает как положительные, так и отрицательные значения. Экстремума нет.

Определение 2. Точки, в которых частные производные равны нулю либо не существуют, называются критическими. Точки, в которых частные производные равны нулю, называются стационарными.

Замечание. Из определения градиента следует, что в стационарных точках градиент является нулевым вектором.