2.3. Основные свойства определённого интеграла

1. Если .

Действительно, .

2. Свойство линейности. Если функции иинтегрируемые наи, то

.

Это свойство вытекает из определения определённого интеграла.

3. .

Это свойство следует из того, что в интегральной сумме все разности меняют знак.

4. .

Действительно, так как .

5. Свойство аддитивности. Если , то

Это следует из определения определённого интеграла, если в качестве точки разбиения взять точку с.

6. Если .

Действительно, так как в интегральной сумме все слагаемые больше или равны нулю.

7. Если на функциииудовлетворяют неравенству, то

.

Действительно, если рассмотреть разность, то с учетом свойства 6, получаем

8. .

Проинтегрировав очевидное неравенство , приходим к данному свойству.

9. Оценка определённого интеграла. Если т и М - наименьшее и наибольшее значения непрерывной функции на, то

Интегрируя неравенство с учетом свойств1 и 7, получаем данное свойство.

10. Теорема о среднем. Если функция непрерывна на, то существует такая точка, для которой выполняется равенство

.

Из свойства 8 получаем неравенство .

Так как непрерывна на, то она принимает все значения, заключенные междут и М. Из этого и следует данное свойство.

2.4. Интеграл как функция верхнего предела

Если в определённом интеграле зафиксировать нижний предел интегрирования, а верхний считать переменным, то интеграл будет являться функцией верхнего предела, где.

Найдем производную этой функции.

Теорема 2 (Барроу). Если непрерывная функция, то

.

Дадим переменной х приращение , тогда

.

По теореме о среднем получаем

, (1)

где .

Из формулы (1) следует, что функция непрерывная, так как

С учетом этой формулы находим производную

что следует в силу непрерывности функции .

Лекция № 30

2.5. Формула Ньютона – Лейбница

Теорема 1. Если функция первообразная для функции, то

. (1)

С учетом теоремы Барроу функция будет являться первообразной и тогда из теоремы о первообразных следует

.

Положим в этом равенстве . Тогда имеем

.

Полагая , получаем формулу Ньютона – Лейбница

.

Пример 1. Оценить .

Для подынтегральной функции нетрудно найти: и. Тогда

Теперь вычислим интеграл непосредственно по формуле Ньютона – Лейбница

т.е.

Пример 2. Найти среднее значение функции на отрезке.

По теореме о среднем имеем

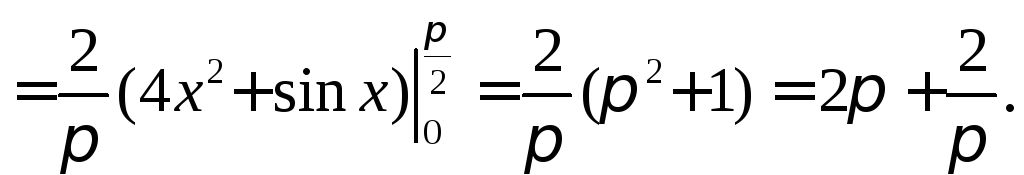
2.6. Замена переменной в определённом интеграле

Пусть дан интеграл , где подынтегральная функциянепрерывна на. Рассмотрим функцию , которая имеет непре-рывную производную наи.

Тогда имеет место формула замены переменной в определённом интеграле

(2)

Докажем эту формулу.

С одной стороны

а с другой стороны

Замечание 1. Аналогично, как и для неопределённого интеграла, часто более удобно использовать замену .

Замечание 2. При вычислении определённого интеграла по формуле (2) не нужно возвращаться к “старой“ переменной.

Замечание 3. Полезно отметить свойства определённого интеграла от четных и нечетных функций в симметричных пределах интегрирования:

1. Если  четная функция, то

(Далее по определению четной функции) =

2. Если нечетная функция, то

(Далее по определению нечетной функции) = 

Пример 3. Вычислить .

Сделаем замену .

Тогда для нижнего предела интегрирования получаем, а для верхнего предела интегрирования.

Пример 4. Вычислить .