2.4. Производная по направлению

Рассмотрим функцию трёх переменных, заданную в некоторой пространственной областиz

V и точку . V

Проведём из точки М вектор ,

направляющие косинусы которого M

. На векторе

возьмём точку ,y

тогда 

расстояние между точками М и М₁. x

Приращение функции будет иметь вид

,

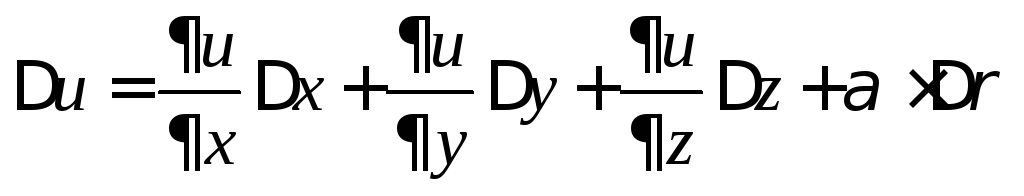где . Если разделить это равенство наи перейти к пределу при, то получим

. (1)

Формула (1) представляет собой производную функции по направлению вектора.

Замечание 2. Частные производные – это частный случай производных по направлению векторов: .

Замечание 3. На плоскости производная по направлению имеет вид

.

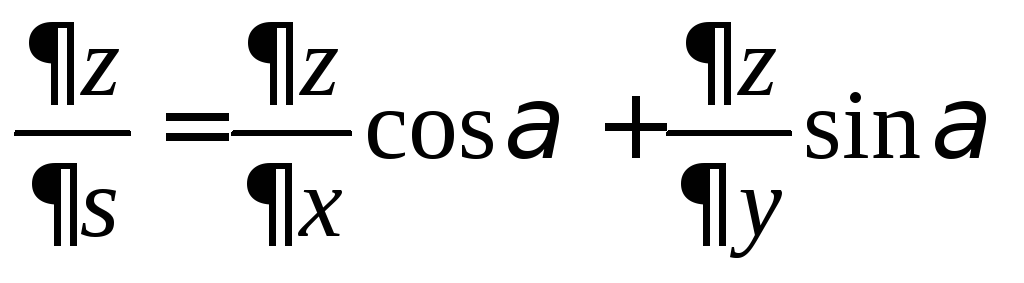Пример 4. Найти производную по направлению в точке от функциипо направлению вектора.

Вычислим частные производные в точке М:

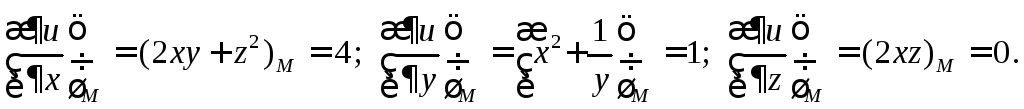
Определим направляющие косинусы вектора :

.

Тогда .

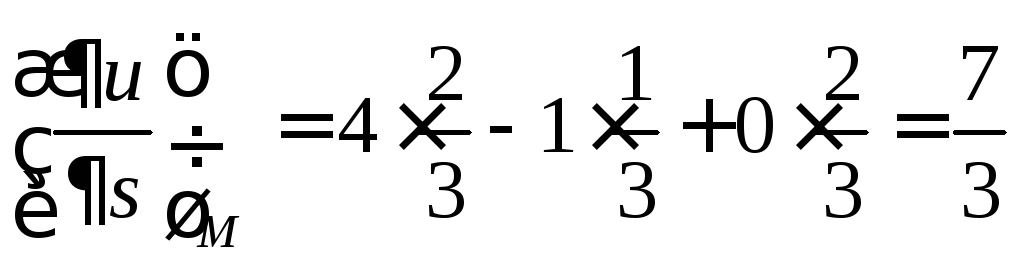2.5. Градиент функции

Рассмотрим функцию трёх переменных.

Определение 1. Совокупность точек, удовлетворяющих уравнению , где, образует поверхность, которая называетсяповерхностью уровня.

Пример 5. Найти поверхности уровня функции .

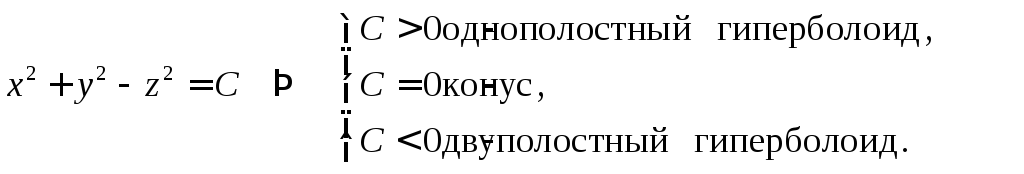
Замечание 4. Для функции двух переменных имеем уравнениялинии уровня .

Определение 2. Вектор 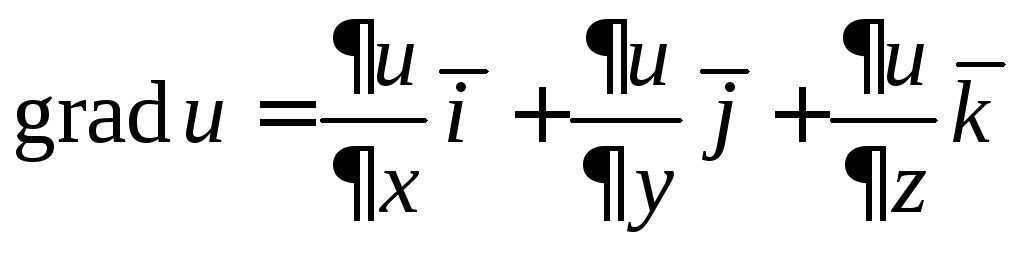называетсяградиентом функции .

Замечание 5. Для функции двух переменных градиент имеет вид.

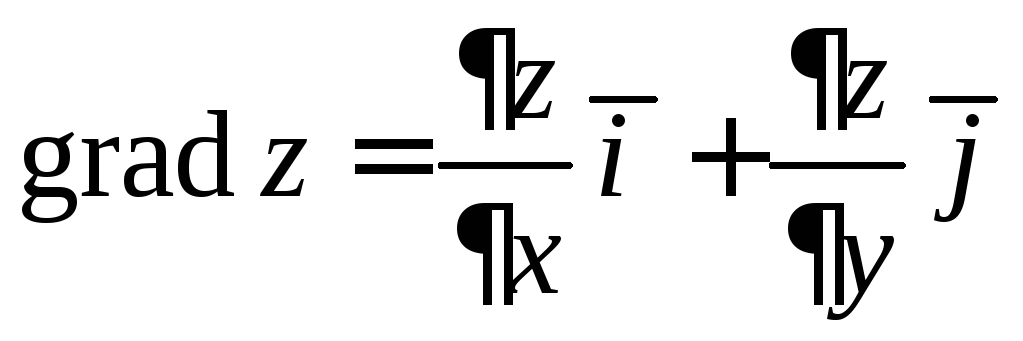Основные свойства градиента:

1. Производная по направлению равна проекциина, т.е..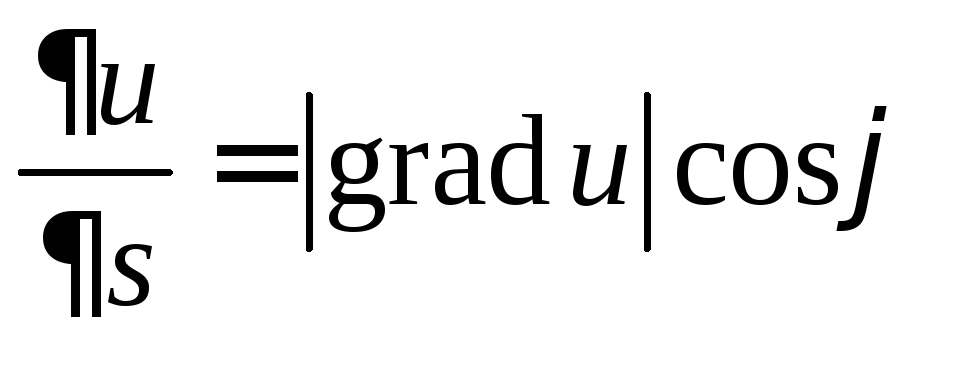

Так как единичным вектором

для вектора будет вектор

,

то

что и требовалось доказать.

2. Производная по направлению в данной точке имеет наибольшее значение, если направление вектора совпадает с направлением градиента.

Это следует из свойства 1, так как 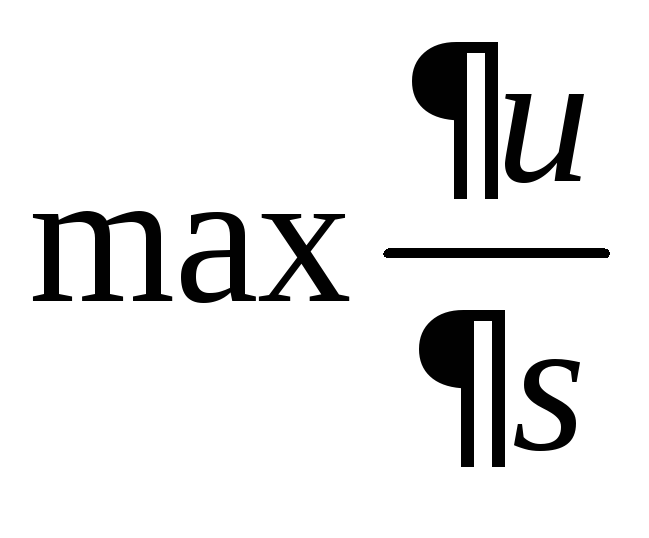будет при.

3. Производная по направлению, перпендикулярному градиенту, равна нулю. Это свойство также следует из свойства 1, так как

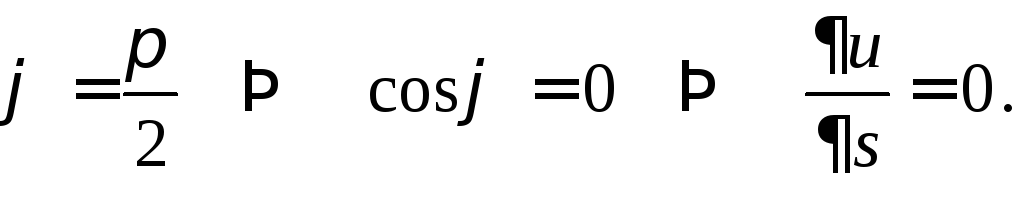
4. Градиент направлен перпендикулярно к поверхности уровня.

Пример 6. Найти градиент функции в точке.

Находим частные производные:

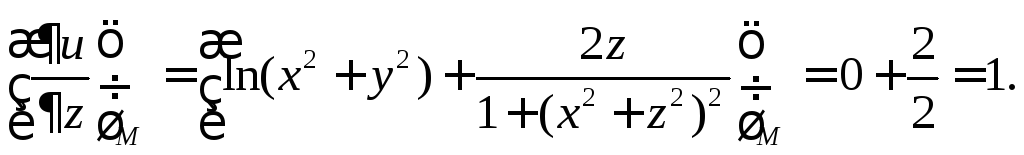
Тогда .

Лекция № 35

2.6. Касательная и нормаль к поверхности

Пусть поверхность задана уравнением. Это уравнение можно рассматривать как уравнение поверхности уровня функциипри, и тогда нормаль

на основании свойств градиента

получаем уравнение нормали

в точке

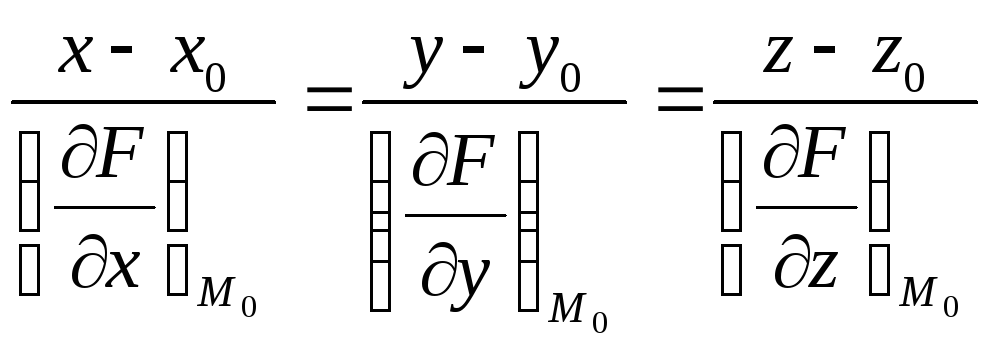Р

и уравнение касательной плоскости Р

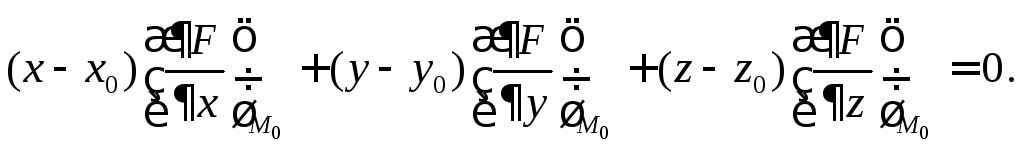
Замечание 1. Если поверхность задана уравнением , то её можно представить в виде

и тогда уравнение нормали

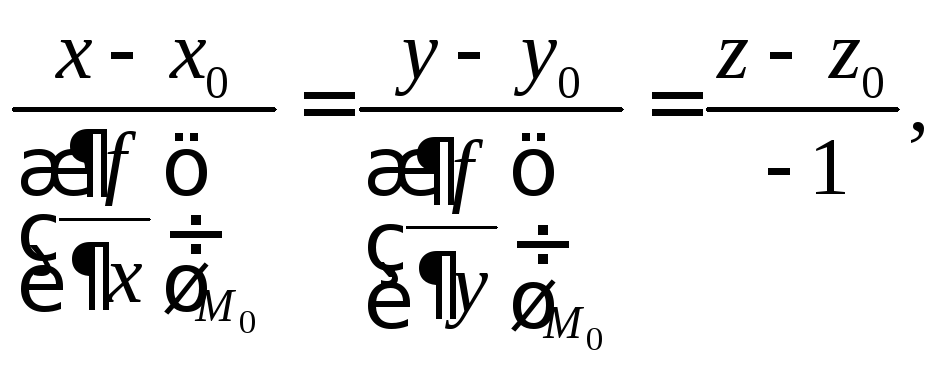
а уравнение касательной плоскости

.

Пример 1. Составить уравнения касательной плоскости и нормали к сфере в точке.

Вычислим частные производные в этой точке:

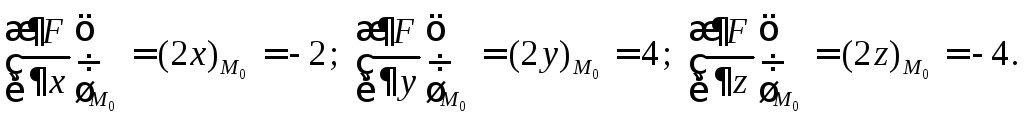
Тогда получаем уравнение нормали

,

а уравнение касательной плоскости –

или .

Тема 3* : Векторная функция скалярного аргумента

3.1. Векторная функция. Предел. Непрерывность

Аналогично, как и для плоской линии, пространственная линия может быть задана параметрическими уравнениями вида

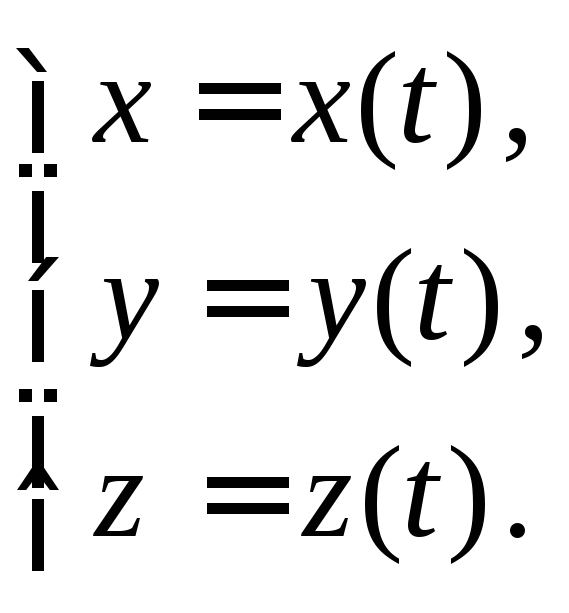
Например, 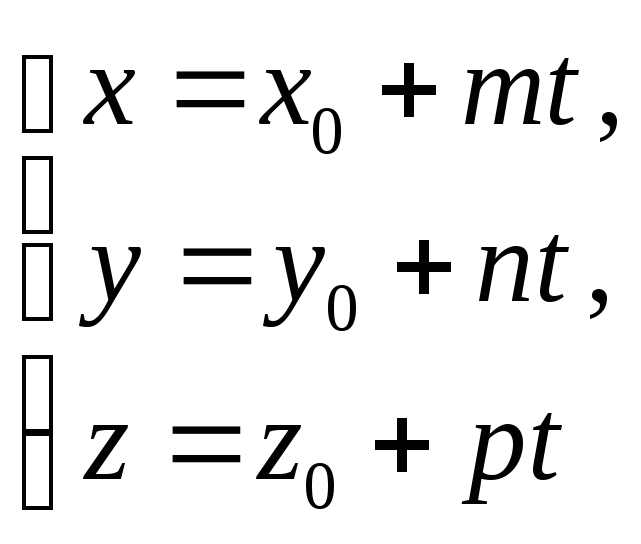– уравнения прямой в пространстве, а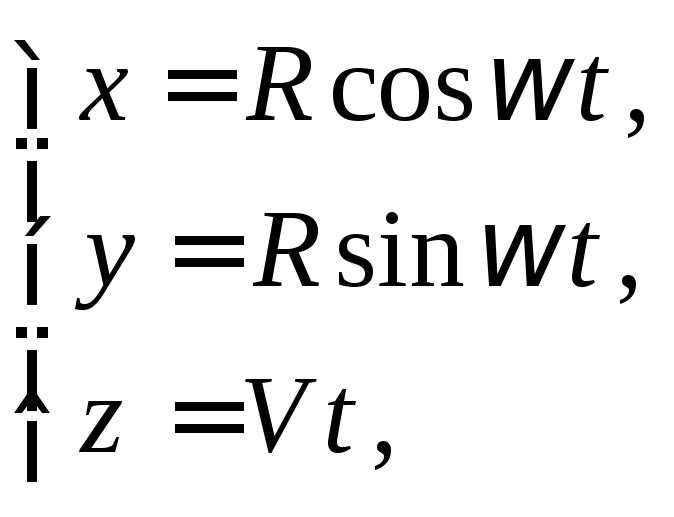, где уравнения винтовой линии (спираль).

Замечание 2. В механике под параметром t подразумевается время.

Рассмотрим радиус-вектор , координаты которого являются функциями параметраt

. (1)

Каждому значению параметраt по формуле (1) соответствует определённый вектор , т.е.является функцией скалярного аргументаt. Таким образом, векторная функция скалярного аргумента записывается в виде . z

Определение. Линия, описанная годограф

концом вектора , называется

годографом векторной функции

.

Предел и непрерывность векторной y

функции определяется через скалярные х

функции .

Если существуют пределы:

то , где.

Аналогично определяется непрерывность векторной функции через непрерывность функций .