1.2. Предел и непрерывность функции двух переменных

Точка стремится к точке, если расстояние между этими точками стремится к нулю, т.е.. Это очевидно эквивалентно: .

Определение 5. Число А называется пределом функции при стремлении точки, если, для всех точек из которой выполняется неравенство, и пишут

или .

Аналогично устанавливается понятие о бесконечном пределе функции. В случае, когда или, неравенствозаменяется неравенствами вида: илисоответственно, гдеМ  произвольное положительное число, и пишут

или .

Определение 6. Функция имеет пределом числоА при иесли, чтоприи пишут

.

Определение 7. Функция называется непрерывной в точке М₀, если имеет место равенство

.

Если в некоторой точке условие непрерывности не выполняется, такая точка называется точкой разрыва.

Пример 4. Исследовать на непрерывность функцию 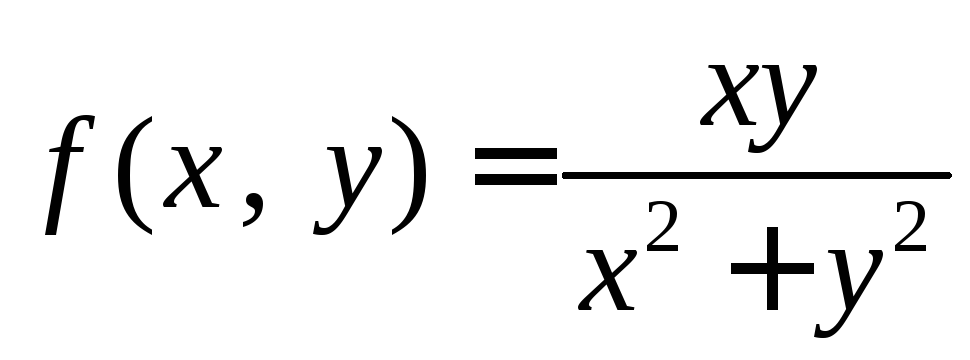в точке

Рассмотрим значения функции вдоль прямых при

.

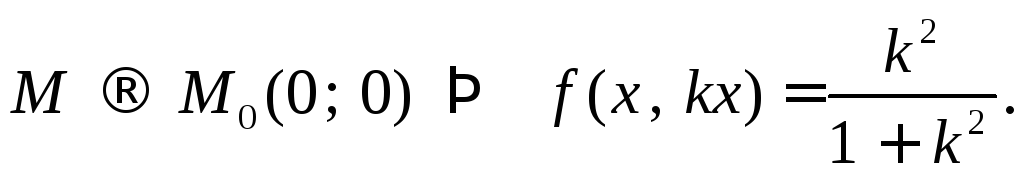Таким образом, функция принимает разные значения в зависимости от значения k. Точка является точкой разрыва.

Замечание. Свойства непрерывной функции двух переменных аналогичны соответствующим свойствам функции одной переменной.

1.3. Частные производные функции двух переменных

Дадим независимой переменной х приращение , тогда функцияполучит приращение, которое называетсячастным приращением z по х и обозначается

.

Аналогично определяется частное приращение z по у:

.

Если же приращение получают одновременно х и у, то приращение

называется полным.

Определение 8. Частной производной от функции пох называется предел

,

или другие обозначения: .

Аналогично, ,

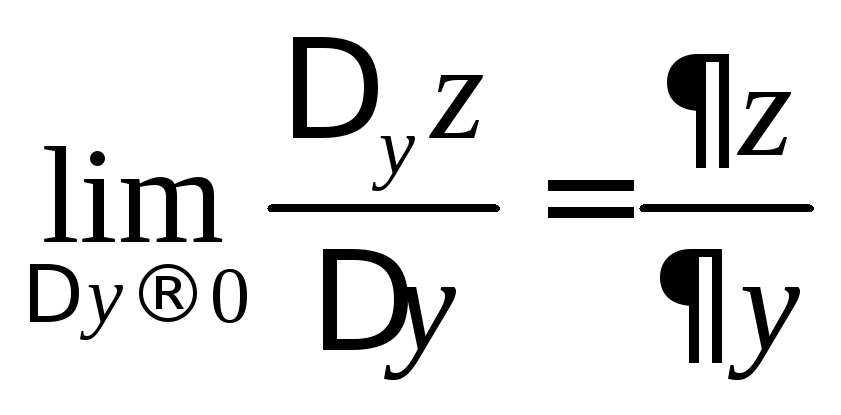или .

Из этих определений следует, что правила вычисления частных производных совпадают с правилами для функции одного переменного. При этом, например, если мы вычисляем производную , то в процессе дифференцирования считаем, что

Пример 5. Найти и, если

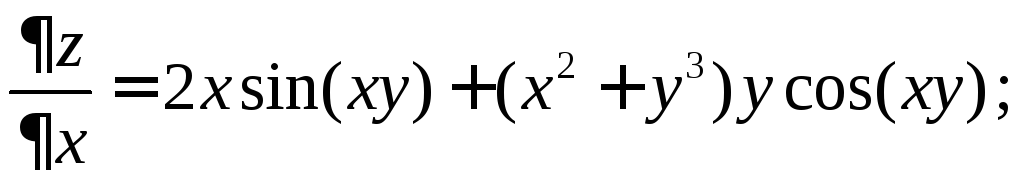
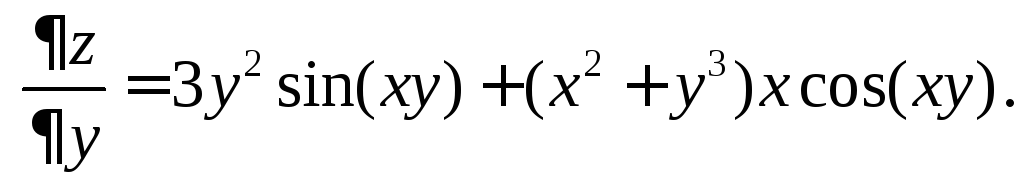
1.4. Полный дифференциал функции двух переменных

Как известно, полное приращение функции определяется по формуле

.

Пусть имеет непрерывные частные производные. Полное приращение представим в виде

.

К каждой разности применим теорему Лагранжа

,

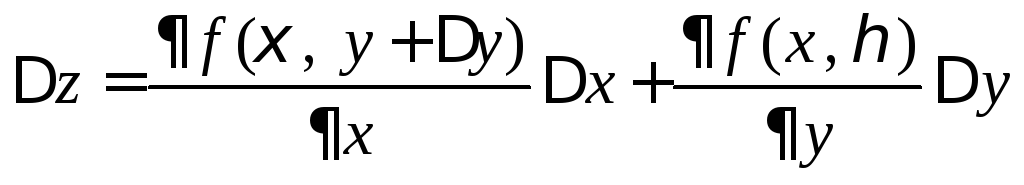где .

Так как в силу непрерывности существуют пределы:

; ,

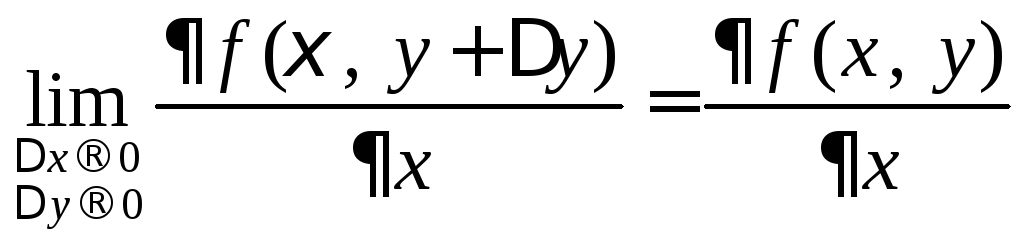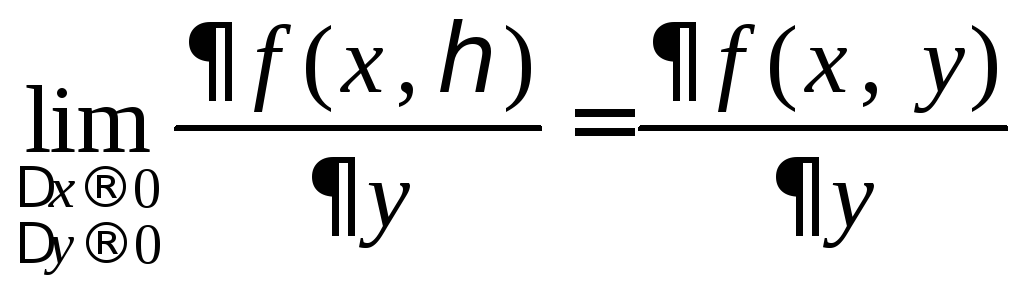то по теореме о пределе функции получим

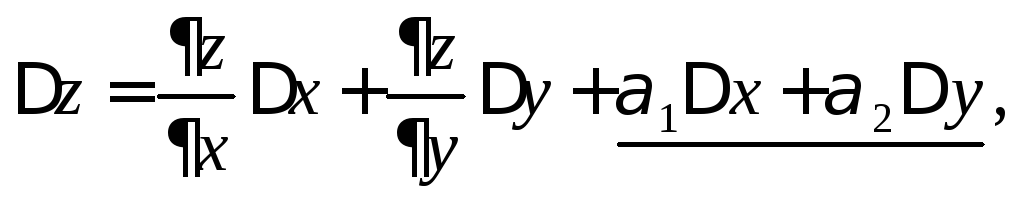
где .

Это означает, что подчеркнутое слагаемое является б.м.в. при и тогда

,

где .

Таким образом, получаем определение дифференцируемой функции двух переменных.

Определение 8. Функция называется дифференцируемой в точке, если её приращение можно представить в виде суммы двух слагаемых, линейных относительноии величины бесконечно малой высшего порядка относительно, т.е.

При этом линейная часть называетсяполным дифференциалом и обозначается

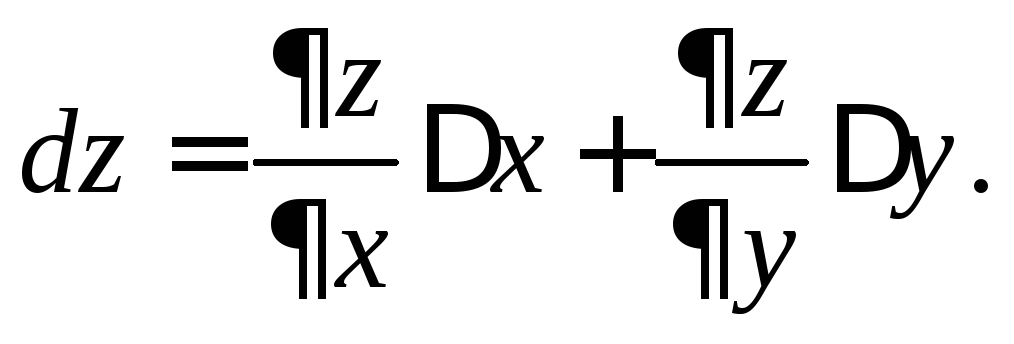
Так как приращения независимых переменных называются их дифференциалами, то окончательно

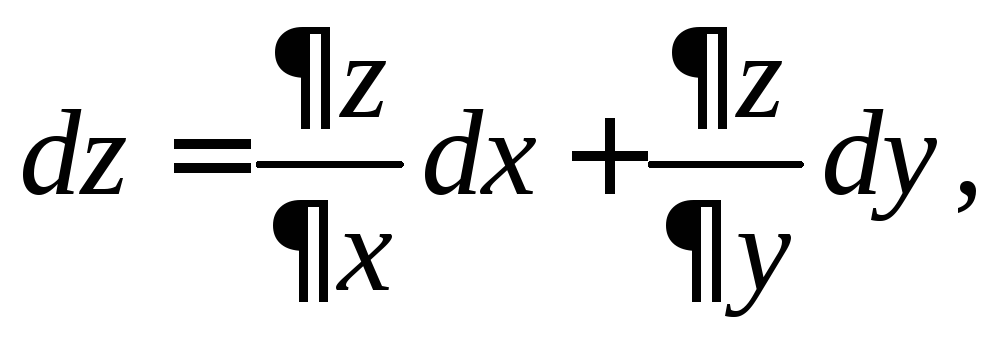
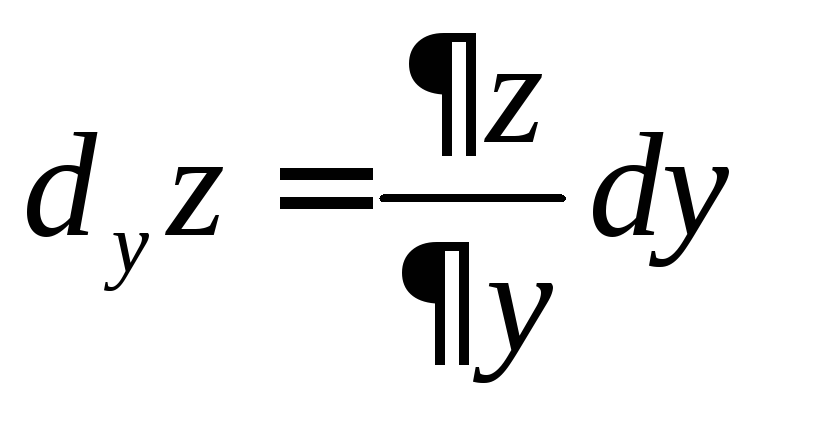
а  частные дифференциалы.

1.5. Производная сложной функции

Пусть задана функция , где. В этом случаеz является сложной функцией аргументов х иу. Пусть все эти функции имеют непрерывные частные производные.

Дадим переменной х приращение , тогда

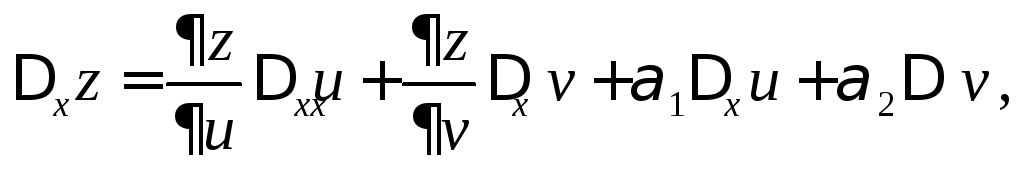
где .

Разделим данное равенство на и перейдём к пределу при

Отсюда следует .

Аналогично получим .

Пример 6. Найти и, если

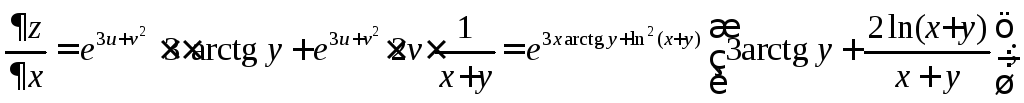
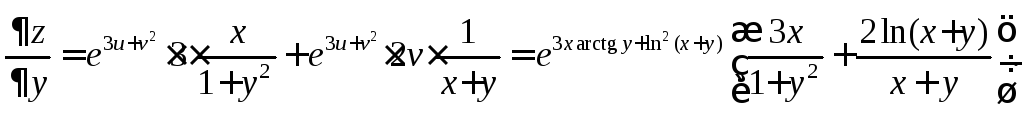
Лекция № 34. Тема 2 : Частные производные.

Производная по направлению. Градиент

2.1. Полная производная

Пусть дана функция , где. Тогда, обобщая формулу для случая производной функции двух переменных, получаем

. (1)

Формула (1) называется формулой полной производной.

Пример 1. Найти полную производную функции , если.

.

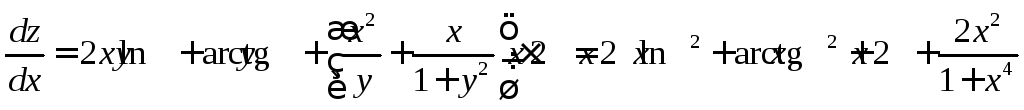2 .2 . Частные производные функции, заданной неявно

Требуется найти частные производные и, если, где. Воспользуемся правилом дифференцирования сложной функции для случая трёх переменных

.

Аналогично находим .

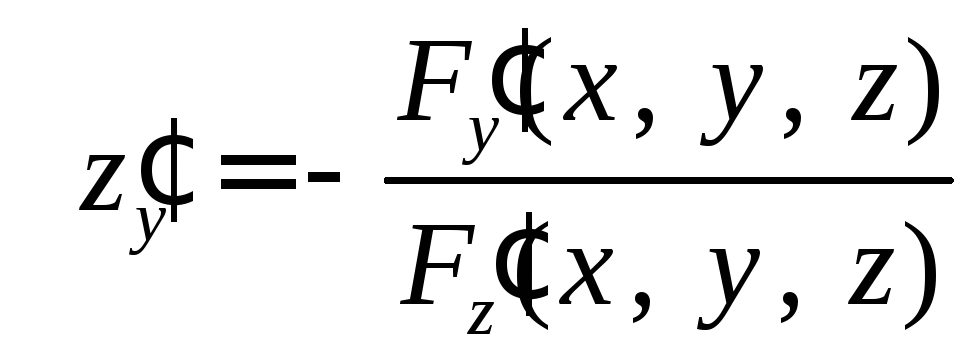Замечание 1. Отсюда следует ранее рассмотренный случай для функции одной переменной: Если , где.

Пример 2. Найти частные производные функции, заданной неявно

.

2.3. Частные производные высших порядков

Рассмотрим функцию . Если частные производныеиявляются дифференцируемыми функциями, то от них можно снова находить частные производные. Частные производные второго порядка определяются следующим образом

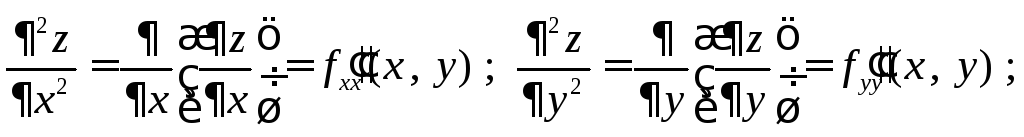
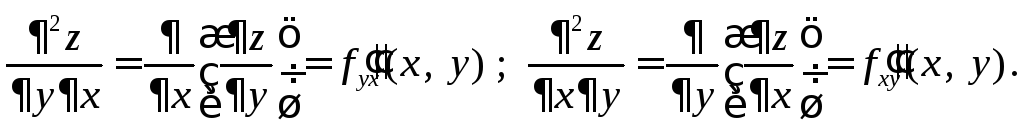
Последние две производные называются смешанными производными второго порядка.

Аналогично определяются производные высших порядков. Например,

означает, что функция сначала дифференцируетсят раз по х, а затем п  т раз по у.

Пример 3. Найти смешанные производные второго порядка функции .

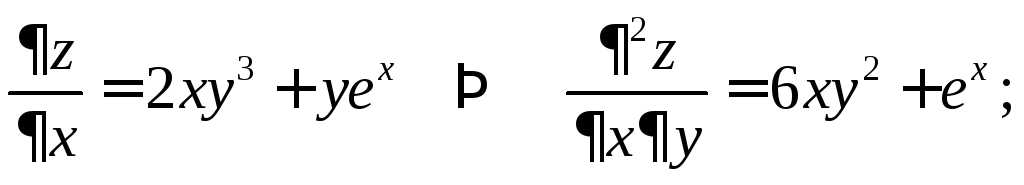
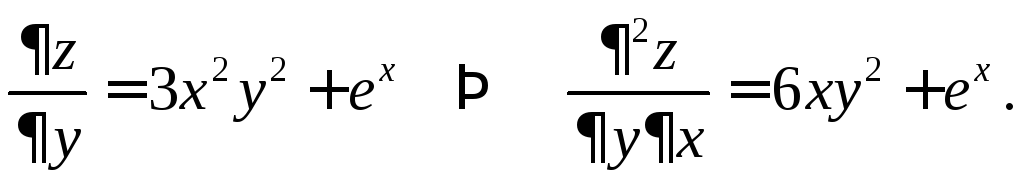
Получено равенство двух смешанных производных второго порядка. Зависит ли в общем случае результат дифференцирования от порядка дифференцирования?

Теорема. Если функция и ее частные производныеопределены в некоторой окрестности точкиМ и непрерывны, то в этой окрестности смешанные производные равны

.