
- •Лекция № 45. Тема 1 : Числовой ряд. Необходимый признак сходимости
- •1.2. Необходимый признак сходимости. Гармонический ряд
- •Тема 2 : Достаточные признаки сходимости рядов с положительными членами
- •2.1. Признаки сравнения
- •Лекция № 46
- •2.2. Признак Даламбера
- •2.3. Радикальный признак Коши
- •2.4. Интегральный признак Коши
- •Тема 3 : Знакопеременные ряды
- •3.1. Знакочередующиеся ряды. Теорема Лейбница
- •3.2. Абсолютная и условная сходимость
- •Лекция № 47. Тема 4 : Функциональные ряды
- •4.1. Определение функционального ряда
- •4.2. Равномерная сходимость функциональных рядов
- •Тема 5 : Степенные ряды
- •5.1. Определение степенного ряда. Теорема Абеля
- •Лекция № 48
- •5.2. Разложение функций в степенные ряды
- •5.3. Применение рядов Тейлора
- •Лекция № 49. Тема 6 : Ряды Фурье
- •6.1. Определение ряда Фурье
- •6.2. Условия разложения функции в ряд Фурье
- •Лекция № 50
- •6.4. Ряды Фурье для четных и нечетных функций
- •6.5. Разложение непериодических функций в ряд Фурье
- •6.6. Интеграл Фурье
- •Уравнения математической физики Лекция № 51.
- •1. Основные типы уравнений математической физики
- •2. Решение волнового уравнения методом Фурье
- •Кратные интегралы Лекция № 52. Тема 1: Определение кратного интеграла
- •1.1. Задачи, приводящие к понятию кратного интеграла
- •1.2. Определение кратного интеграла и его основные свойства
- •Тема 2: Двойной интеграл
- •2.1. Определение двойного интеграла (ди)
- •2.2. Вычисление двойного интеграла.
- •Лекция № 53
- •2.3. Замена переменных в двойном интеграле.
- •2.4. Ди в полярной системе координат
- •2.5. Приложения двойного интеграла
- •Лекция № 54
- •Лекция № 55. Тема 3 : Тройной интеграл
- •3.1. Определение и вычисление тройного интеграла
- •3.2. Замена переменных в тройном интеграле
- •3.3. Приложения тройного интеграла
- •Лекция № 56. Тема 4 : Криволинейные интегралы
- •4.1. Криволинейные интегралы первого рода или по длине дуги
- •4.2. Криволинейные интегралы второго рода или по координатам
- •Лекция № 58.
- •4.3. Формула Грина
- •4.4. Условие независимости криволинейного интеграла второго рода от пути интегрирования
- •Тема 5 : Поверхностные интегралы
- •5.1. Поверхностные интегралы первого рода
- •5.2. Поверхностные интегралы второго рода
- •5.3. Приложения поверхностных интегралов
- •Лекция № 58. Тема 6 : Элементы теории поля
- •6.1. Понятие поля
- •6.2. Формула Гаусса Остроградского
- •6.3. Формула Стокса
- •Теория вероятностей Лекция № 59. Тема 1 : Общие понятия
- •1.1. Предмет теории вероятностей
- •1.2. Пространство элементарных событий
- •1.3. Операции над событиями
- •1.4. Статистический подход к понятию вероятности
- •Лекция № 60
- •1.5. Элементы комбинаторики
- •1. Перестановки.
- •2. Сочетания.
- •3. Размещения.
- •1.6. Классическое определение вероятности
- •1.7. Аксиоматическое определение вероятности
- •Лекция № 61. Тема 2 : Основные теоремы теории вероятностей
- •2.1. Теорема умножения вероятностей
- •2.2. Теорема сложения вероятностей
- •2.3. Формула полной вероятности
- •2.4. Формула Бейеса
- •Лекция № 62. Тема 3 : Повторение испытаний
- •3.1. Независимые испытания. Формула Бернулли
- •3.2. Локальная теорема Муавра – Лапласа
- •3.3. Интегральная теорема Лапласа
- •3.4. Теорема Пуассона
- •3.5. Вероятность отклонения частоты от постоянной вероятности в независимых испытаниях
- •Лекция № 63.
- •Тема 4 : Случайные величины и функции распределения
- •4.1. Случайные величины
- •4.2. Функция распределения вероятностей для дискретной св
- •4.3. Непрерывная св. Функция распределения
- •Лекция № 64. Тема 5 : Числовые характеристики св
- •5.1. Математическое ожидание св
- •5.2. Дисперсия и среднее квадратическое отклонение св
- •5.3. Понятие о моментах св
- •Лекция № 65. Тема 6 : Основные законы распределения св
- •6.1. Законы распределения дискретных случайных величин
- •6.1.1. Биномиальное распределение
- •6.1.2. Распределение Пуассона
- •6.1.3. Геометрическое распределение
- •6.2. Законы распределения непрерывных случайных величин
- •6.2.1. Равномерное распределение
- •6.2.2. Показательное распределение
- •Лекция 66
- •6.2.3. Нормальное распределение
- •Тема 7 : Закон больших чисел
- •7.1. Неравенство Чебышева
- •7.2. Теорема Чебышева
- •Лекция № 67. Тема 8 : Многомерные случайные величины
- •8.1. Многомерные св и их функции распределения
- •8.2. Числовые характеристики двумерной св
- •Элементы математической статистики Лекция № 68. Введение
- •1. Предмет математической статистики
- •Тема 1: Статистические законы распределения выборки
- •1.1. Полигон и гистограмма
- •1.2. Эмпирическая функция распределения
- •Тема 2 : Статистические оценки параметров распределения
- •2.1. Точечные оценки
- •2.2. Интервальные оценки
- •Лекция № 69
- •Тема 3 : Проверка статистических гипотез. Критерий согласия Пирсона
- •Тема 4 : Элементы теории корреляции
- •4.1. Статистические зависимости
- •4.2. Линейная регрессия
- •4.3. Корреляционная таблица
- •4.4. Выборочный коэффициент корреляции
Лекция № 64. Тема 5 : Числовые характеристики св
5.1. Математическое ожидание св
Часто на практике закон распределения неизвестен и приходится ограничиваться неполными сведениями о СВ. Тогда полезно использовать некоторые параметры, которые суммарно описывают СВ. Такие параметры называются числовыми характеристиками. К их числу, в частности, относится математическое ожидание.
5.1.1. Рассмотрим случай дискретной СВ.
|
X |
|
|
… |
|
|
p |
|
|
… |
|
Обозначим её среднее значение через М(Х), тогда
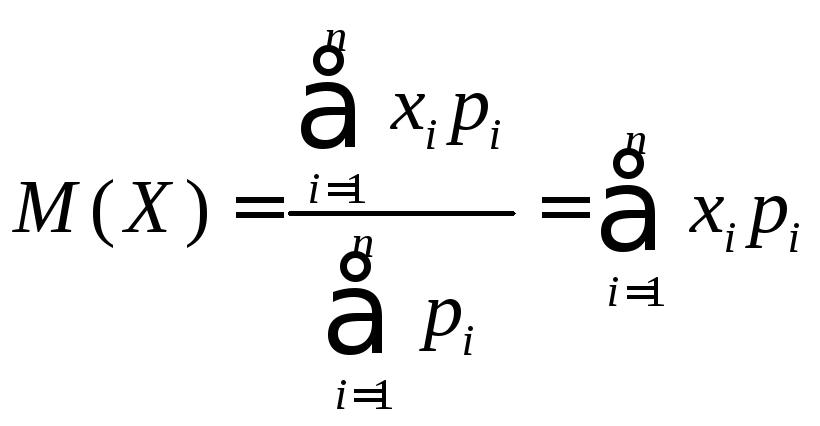 ,
,
так как
![]() .
.
Определение 1. Математическим ожиданием дискретной СВ называ-ется величина
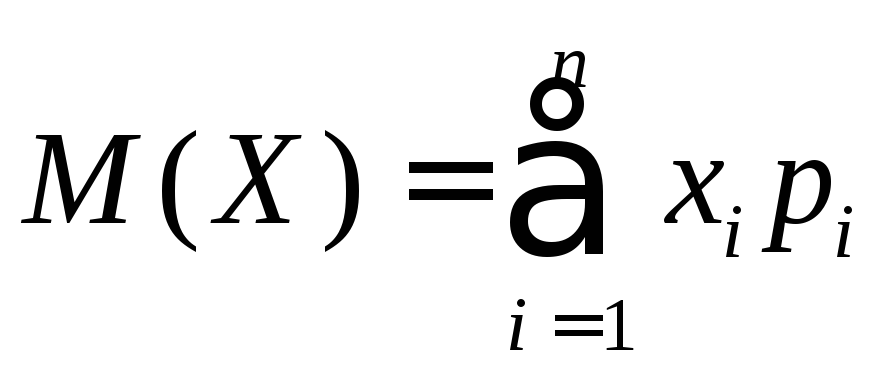 .
(1)
.
(1)
Замечание. Если число возможных значений дискретной СВ беско-нечно, то
 ,
,
при условии сходимости ряда.
Из определения математического ожидания следуют его свойства:
1. Если
![]() .
.
2. Если
![]() .
.
3.
![]() .
.
Действительно, рассмотрим две СВ с законами распределения
|
X |
|
|
… |
|
p |
|
|
… |
|
Y |
|
|
… |
|
q |
|
|
… |
Тогда СВ
![]()
принимает возможные значения
принимает возможные значения
![]() с вероят-ностью
с вероят-ностью![]() и тогда
и тогда
![]()
![]() .
.
4. Если Х
и Y
независимые СВ, то
![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
Следствие.
![]() .
.
Пример 1. Найти математическое ожидание числа очков, которые могут выпасть при бросании двух игральных костей.
Пусть Х и Y СВ выпадения очков на двух костях соответственно:
|
X |
1 |
… |
6 |
|
p |
|
… |
|
|
Y |
1 |
… |
6 |
|
p |
|
… |
|
Тогда
 .
.
5.1.2. Для непрерывной
СВ выражение
![]() представляет собой среднее значение
этой СВ на интервале длиной
представляет собой среднее значение
этой СВ на интервале длиной![]() и тогда её среднее значение
и тогда её среднее значение
 .
(2)
.
(2)
Замечание. Математическое ожидание непрерывной СВ имеет анало-гичные свойства.
5.2. Дисперсия и среднее квадратическое отклонение св
Математическое ожидание полностью не характеризует СВ. Поэтому вводят другие числовые характеристики.
Определение 2. Отклонением или центрированной СВ называется вели-
чина
![]() .
.
Легко показать,
что
![]() .
.
Определение 3.
Дисперсией СВ называется математическое
ожидание квадрата отклонения случайной
величины Х
от своего математического ожидания
![]() и обозначается
и обозначается
![]() .
.
Из этого определения следует, что дисперсия характеризует меру рассеивания возможных значений около её математического ожидания.
Определение 4.
Величина
![]() называется средним квадра-тическим
отклонением.
называется средним квадра-тическим
отклонением.
Получим более удобную формулу для вычисления дисперсии.
![]() .
(3)
.
(3)
Тогда для дискретной СВ формула для вычисления дисперсии примет вид
![]() или
или
![]() .
(4)
.
(4)
Для непрерывной СВ -
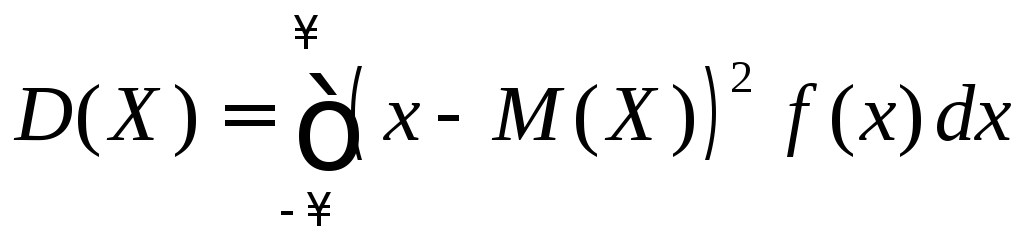 или
или
 .
(5)
.
(5)
Свойства дисперсии:
1.
![]() ,
как сумма неотрицательных членов, или
как интеграл от неотрицательной
функции.
,
как сумма неотрицательных членов, или
как интеграл от неотрицательной
функции.
2.
![]() ,
так как
,
так как![]() .
.
3.
![]() ,
что следует непосредственно из определения
дисперсии.
,
что следует непосредственно из определения
дисперсии.
4.
Если Х
и Y
независимые СВ, то
![]() .
.
Действительно,
![]()
![]()
(с учетом свойств
математического ожидания)
![]()
![]()
Пример 2.
Найти математическое ожидание
![]() ,
дисперсию
,
дисперсию![]() и среднеквадратическое отклонение
и среднеквадратическое отклонение![]() случайной величины с плот-ностью
распределения
случайной величины с плот-ностью
распределения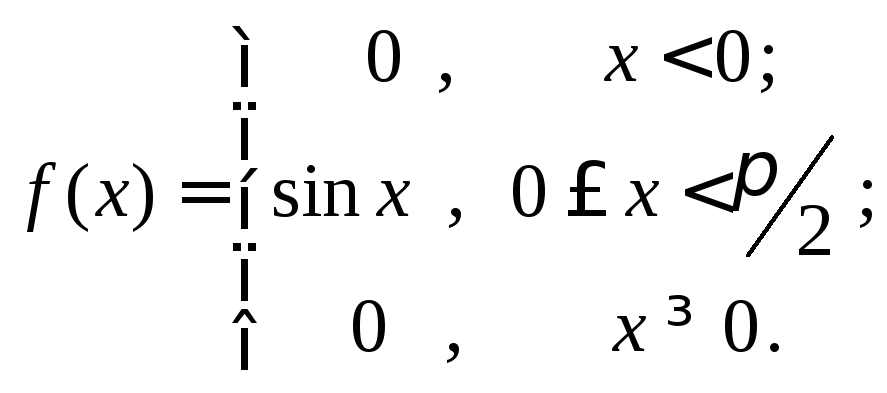
По формулам (2), (4-5) соответственно находим:

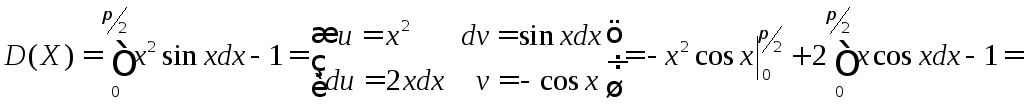
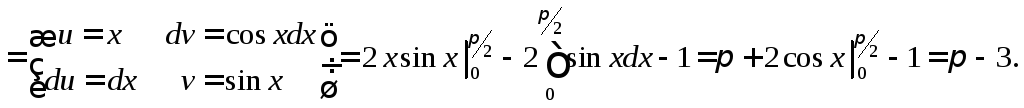
![]() .
.
