
- •Предмет начертательной геометрии
- •Историческая справка
- •Метод проекций
- •объект проектирования
- •центр проектирования
- •поверхность (плоскость) проектирования
- •Свойство центральной проекции
- •невозможно
- •цилиндрическим
- •коническим
- •прямоугольным
- •Следы плоскости
- •собирательным
- •перпендикулярны
- •линии уровня
- •Линии уровня
- •Построение точки на плоскости, заданной следами.
- •Теорема:
- •Следствие:
- •Определение:
- •Пример
- •Обратная задача
- •Решение
- •Примечание
- •Пример
- •Пример
- •Задача 1
- •Решение:
- •Задача 2
- •Решение:
- •Задача 3
- •Решение:
- •Задача 4
- •Решение:
- •Свойства:
- •Следствия:
- •Пример 7.2
- •Пример 7.3:
- •Решение:
- •Пример 7.4
- •Решение:
- •Пример 7.5
- •Решение:
- •Пример 7.6
- •Решение:
- •Пример 7.7
- •Решение:
- •Пример 7.8
- •гранями
- •способом ребер
- •Пример 8.1
- •Пример 8.2
- •Пример 8.3
- •Пример 8.4
- •Прямой круговой цилиндр
- •Сечения цилиндра
- •– окружность;
- •основанию – эллипс;
- •Сечения конуса (конические сечения) (
- •– окружность;
- •– эллипс;
- •парабола
- •Сфера
- •окружность
- •Пример 9.1
- •Пример 9.2
- •Пример 9.3
- •Пример 9.4
- •Построение развертки
- •Пример 9.5.
- •Пример 10.1
- •Пример 10.2
- •Пример 10.3
- •Пример 10.4
- •Теорема Монжа
- •Пример 11.1
- •Пример 11.3
- •Двойная точка
- •Точка перегиба
- •Точка излома (угловая точка)
- •Точки возврата первого рода
- •Узловая (многоразовая) точка
- •Цилиндрическая винтовая линия.
- •Построение проекций винтовой линии.
- •Построение касательной плоскости
- •Пример 12.1
- •Пример 12.2
- •Ошибка! Источник ссылки не найден.
- •Пример 12.3
- •Кинематический способ
- •Каркасный способ
- •определителя
- •Геометрическую часть
- •Алгоритмическая часть
- •класса
- •Класс I
- •Класс II
- •Подкласс 1
- •Подкласс 2
- •Подкласс 3
- •Подгруппа а
- •Подгруппа б.
- •Подгруппа 3
- •Подгруппа
- •Подгруппа
- •Группа
- •Группа
- •Прямой цилиндроид
- •Прямой коноид
- •Косая плоскость
- •Плоскость
- •Торсы
- •коническая поверхность (
- •цилиндрическая поверхность (
- •плоскость
- •Меридиан
- •Параллель
- •сферу
- •сжатый
- •эллипсоид
- •двуполостный гиперболоид вращения
- •однополостный гиперболоид вращения
- •параболоид вращения
- •гелисой
- •геликоидами
- •Косой геликоид
- •комплекс
- •конгруэнция
- •связкой
|
l2 |
|
А2 |
h |
|
|
2 |
|
|
f2 |
|
x |
|
|
|
h1 |
|
A1 |
f1 |
|
l1 |
||
|
||
Рис. 5.5 Перпендикулярность прямой и |
||
|
плоскости |
|
Обратная задача: через
(.)А провести плоскость Θ l, заданной ее проекциями l1 и l2 (Рис. 5.5).
Решение: провести через
(.)А пару прямых, одна из которых фронталь и фронтальной проекции линии l, другая горизонталь и горизонтальной проекции линии l.
Частный случай: перпендикуляр к проектирующей плоскости является линией уровня по отношению к соответствующей ПП (Рис. 5.6). Т.е., перпендикуляр к фронтально-проектирующей плоскости является фронталью,..
|
|
|
|
|
S2 |
|
|
|
f |
|
|
|
|
|
|||
2 |
|
|
|
|
|
S ^ П |
ü |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
ý |
Þ f // П2 |
|
|
|
|
|
|
f ^ S |
||
|
|
|
|
|
|
þ |
|
|
|
|
|
|
|
|
|
|
|
x
f1
Рис. 5.6 Перпендикуляр к проектирующей плоскости
51
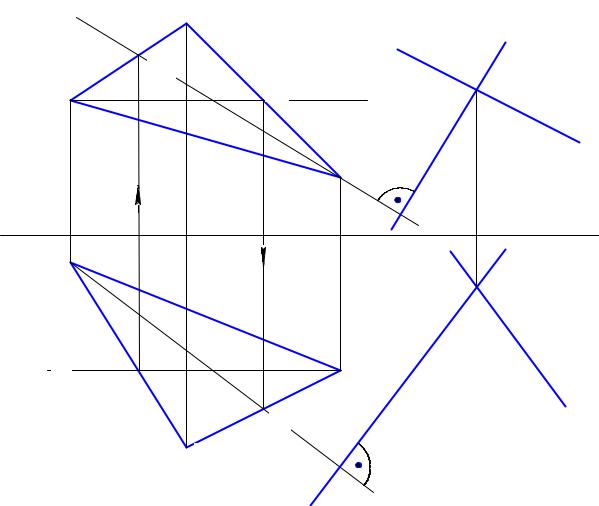
Примечание: прямые, перпендикулярные к плоскостям, используются для определения расстояния между (.) и плоскостью.
5.4Перпендикулярность двух плоскостей
Известно, что плоскость перпендикулярна другой плоскости, если ей принадлежит перпендикуляр к этой плоскости. На этом свойстве основано построение взаимно-перпендикулярных плоскостей.
Пример: построить плоскость Θ, проходящую через (.)М перпендикулярно плоскости (АВС) (Рис. 5.7).
Алгоритм: Первый способ
1. В плоскости Θ строят горизонталь и фронталь;
2. Через (.)М проводят прямую, горизонтальная проекция которой горизонтали, и фронтальная проекция фронтали.
f2 |
|
B |
|
|
|
|
|
2 |
|
|
l2 |
|
22 |
|
|
|
|
А2 |
12 |
h2 |
|
|
|
|
M2 |
m2 |
|||
|
|
|
|||
|
|
|
|
|
|
|
|
|
С2 |
|
|
А1 |
|
|
|
|
l |
|
|
|
|
M1 |
1 |
|
|
|
|
|
|
f1 |
|
|
С1 |
|
m1 |
21 |
|
|
|
||
|
|
|
|
||
|
|
11 |
h |
|
|
|
|
В1 |
1 |
|
|
|
|
|
|
l Æ θ (ABC) |
|
|
|
|
|
|
Рис. 5.7 Перпендикулярные плоскости
3.Через (.)М проводят вторую, как угодно направленную прямую, не совпадающую с перпендикуляром.

Эти две прямые зададут требуемую плоскость.
Пункт 3 алгоритма указывает на то, что через точку можно провести к плоскости бесконечное число перпендикулярных плоскостей, т.е., их пучок. Для того, чтобы плоскость оказалась единственной, необходимо введение дополнительных условий, например, принадлежность искомой плоскости не одной, а двух заданных точек и т.п.
Второй способ (Рис. 5.8).
Проводим через точку М две прямые, одна из которых горизонталь и горизонтальной проекции одной из сторон АВС, другая фронталь и фронтальной проекции той же
стороны АВС.
|
|
M2 |
h2 |
|
В2 |
f2 |
|
|
|
|
q (ABC) Æ å (f Ç h) |
x |
А2 |
С2 |
|
|
|
||
|
|
|
|
|
|
С1 |
|
|
А1 |
|
f1 |
|
|
|
|
|
|
|
|
|
|
h1 |
В1 |
M1 |
||
|
|
|
|
|
|
Рис. 5.8 Перпендикулярные плоскости
53

Пример: Провести через (.) К горизонтально-проектирующую плоскость Σ, плоскости общего положения Θ, заданной следами
(Рис. 5.9).
К2 |
Σ |
f2 |
|
2 |
|
X |
h2 =f1 |
Σ1
K1 h1
Рис. 5.9 Перпендикулярные плоскости
54
Тема 6 |
Метрические |
и |
позиционные |
задачи |
|
начертательной геометрии |
|
||
6.1Позиционные задачи.
Содержание позиционных задач: определение взаимного положения геометрических фигур – точек, прямых, плоскостей.
|
Точка В |
Прямая b |
Плоскость Φ |
|||||||||
|
|
|
|
|
|
|
|
|||||
Точка А |
А=В |
|
Î |
A |
Î |
Φ |
||||||
|
A¹B |
А b |
Ï |
|||||||||
|
|
Ï |
A |
Φ |
||||||||
|
|
|
|
|
A |
b |
|
|
||||
|
A1¹B1 A2ºB2 |
|
|
|
|
|
|
|
|
|||
|
или |
|
|
|
|
|
|
|
|
|||
|
A1ºB1 A2¹B2 |
|
|
|
|
|
|
|
|
|||
|
Конкурирующие |
|
|
|
|
|
|
|
|
|||
|
точки. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
Прямая а |
B |
Î |
a |
a _ b |
a |
Î |
Φ |
|||||
|
Ï |
aêêb |
|
|
||||||||
|
B |
a |
êê |
|
||||||||
|
|
|
|
|
|
a |
|
|
Φ |
|||
|
|
|
|
|
aÇb |
aÇΦ |
||||||
|
|
|
|
|
|
|
|
|
|
|||
Плоскость Θ |
Î |
Θ |
b |
Î |
Θ |
|
|
êê |
||||
|
B |
|
|
Φ Θ |
||||||||
|
BÏΘ |
bêêΘ |
ΦÇΘ |
|||||||||
|
|
|
|
|
bÇΘ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
6.2Метрические задачи
Содержание и цель решения метрических задач начертательной геометрии – определение количественно измеряемых параметров геометрических элементов: расстояний, углов, отображений фигур.
Для решения метрических задач необходимо выбрать или получить построениями такое положение геометрических фигур, при котором искомые элементы отображаются в натуральную величину и могут быть измерены непосредственно метрическим инструментом. Например, геометрические фигуры проектируются без искажения, в натуральную величину и могут быть измерены тогда, когда они лежат в плоскости уровня. Есть другие частные положения фигур, когда необходимые для измерения элементы проектируются без искажения.
55
Ниже рассмотрен набор базовых вариантов положений фигур по отношению к плоскостям проекций, при которых решаются метрические задачи.
6.2.1Прямая.
Отрезок прямой проектируется на ПП в натуральную величину, если он является линией уровня (Рис. 6.1).
A2 |
B |
|
2 |
x |
|
A1 |
|
н.в. |
|
|
B1 |
Рис. 6.1 Линия уровня - горизонталь |
|
6.2.2Треугольник, и другие фигуры на плоскости уровня.
Любая фигура на плоскости уровня проектируется на «свою» плоскость проекций в натуральном виде (в натуральную величину) (Рис. 6.2).
A2 |
B |
C |
|
2 |
2 |
x |
|
|
A1 |
|
|
|
|
C1 |
|
н.в. |
|
|
B1 |
|
Рис. 6.2 Треугольник на горизонтальной плоскости уровня |
||
56
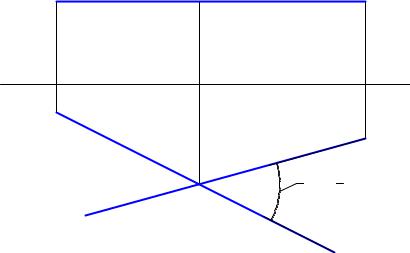
6.3Определение углов
6.3.1Угол пересечения.
Как известно, две пересекающиеся прямые задают плоскость. Если эта плоскость по условию или в результате дополнительных построений заняла положение, параллельное плоскости проекции, тогда она является плоскостью уровня и угол между прямыми на этой плоскости проектируется без искажения, в натуральную величину (Рис. 6.3).
|
A2 |
|
l Ξm |
||
2 |
2 |
|
l1
m1
θн.в.
A1
Рис. 6.3 Угол между прямыми на горизонтальной плоскости уровня
6.3.2Угол скрещивания.
Угол между скрещивающимися прямыми определяется как угол между пересекающимися прямыми, одна из которых задана, а другая получена параллельным переносом второй заданной прямой до пересечения с первой.
Если две скрещивающиеся прямые параллельны плоскости проекции, то есть, являются линиями уровня, тогда угол между ними будет такой же, как и угол между проекциями этих прямых на «свою» плоскость проекций (Рис. 6.4).
57
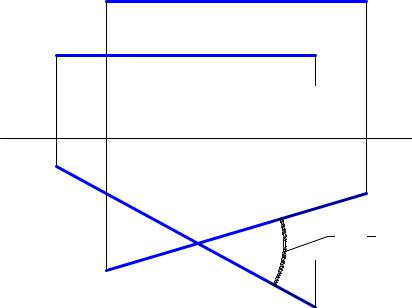
m2 |
l2 |
x |
l1 |
m1 |
δн.в. |
Рис. 6.4 Угол между скрещивающимися прямыми |
6.3.3Прямой угол.
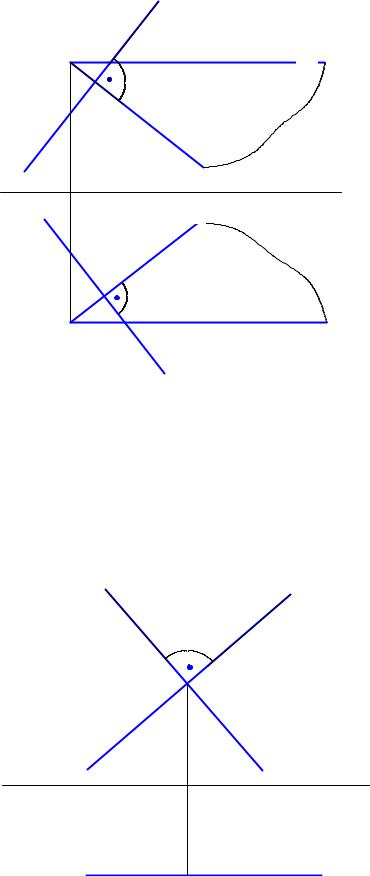
Прямой угол проектируется в натуральную величину, если хотя бы одна сторона этого угла параллельна плоскости проекций, т.е., является линией уровня (см. 5.1).
6.3.4Угол между прямой и плоскостью
Как известно, угол между прямой и плоскостью определяется как угол между прямой и ее проекцией на эту плоскость.
Для того, чтобы угол между прямой и ее проекцией на заданную плоскость отобразился на плоскости проекции в натуральную величину, нужно, чтобы прямая и ее проекция на заданную плоскость были параллельны этой плоскости проекции.
Это возможно в том случае, если заданная плоскость перпендикулярна плоскости проекций, то есть является проектирующей плоскостью, а заданная прямая линией уровня (Рис. 6.5).
58

|
|
E2 |
Рис. 6.5 Угол между |
|
|
|
прямой и плоскостью |
A2 |
|
|
Θ(AEÇAD)^S( ABC); |
|
δ |
|
|
|
|
ΘúúÕ2 Þ å^Õ2 |
|
|
|
|
|
|
B2 |
D2 |
AEÙå = ÐE2A2D2 |
|
|
||
x |
|
C2 |
|
|
|
|
|
|
B1 |
|
|
A1 |
D1 |
E1 |
|
|
|
||
|
|
C1 |
|
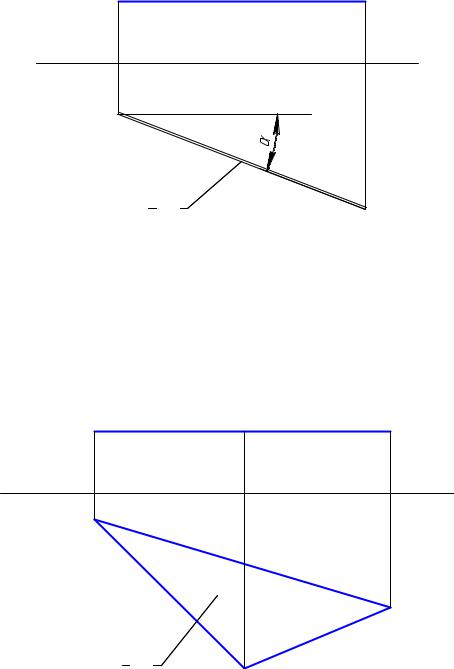
6.3.5 Угол между двумя плоскостями. |
|||
По определению, мерой двугранного угла между двумя плоскостями является линейный угол, образованный двумя линиями пересечения заданных плоскостей третьей плоскостью, перпендикулярной обоим заданным плоскостям. Такая третья плоскость будет перпендикулярна линии взаимного пересечения заданных плоскостей.
Двугранный угол спроектируется на плоскость проекций в натуральную величину, если будет лежать в плоскости, параллельной плоскости проекции. Для этого линия пересечения заданных плоскостей должна быть перпендикулярной этой плоскости проекции. Тогда обе заданные плоскости также будут перпендикулярны к этой плоскости проекции. То есть, для того, чтобы двугранный угол между плоскостями проектировался в натуральную величину, они должны быть проектирующими плоскостями (Рис. 6.6).

|
|
B2 |
l2 |
|
|
|
a2 |
C2
A2
x
|
l1 |
A |
|
1 |
|
|
|
|
|
|
||
|
|
|
|
α |
||
B1 |
|
|
|
|||
|
|
|
н |
в. |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
C1 |
|
|||
|
|
|
|
a1 |
||
|
|
|
|
|||
≡
m2
m1
a = Q( ABC)ÇW(l || m); a P1 Þ Q P1; W P1.
Рис. 6.6 Угол между двумя плоскостями
6.4Определение расстояний
6.4.1Расстояние между двумя точками
Если две точки одинаково удалены от плоскости проекции, т.е. лежат в плоскости, параллельной плоскости проекции, тогда отрезок прямой, соединяющий эти точки спроектируется на плоскость проекции в натуральную величину. Длина проекции отрезка, будучи равной длине самого отрезка, станет мерой расстояния между двумя точками (Рис. 6.7).
A |
B2 |
2 |
|
х |
|
A1 |
н.в. |
|
B1 |
Рис. 6.7 Расстояние между точками |
|
60

6.4.2Расстояние между точкой и прямой
При определении расстояния между точкой и прямой могут быть рассмотрены три типовых случая:
1.Прямая является проектирующей. Тогда перпендикуляр, опущенный из точки на прямую, являющийся мерой расстояния между точкой и прямой, будет параллелен плоскости проекции, т.е. будет линией уровня. Этот перпендикуляр спроектируется на плоскость проекции без искажения и эта проекция будет мерой расстояния между точкой и прямой (Рис. 6.8).
|
l2 |
A |
B2 |
2 |
|
х |
|
A1 |
н.в. |
|
B1 ≡l1 |
Рис. 6.8 Расстояние от точки до прямой. Случай 1
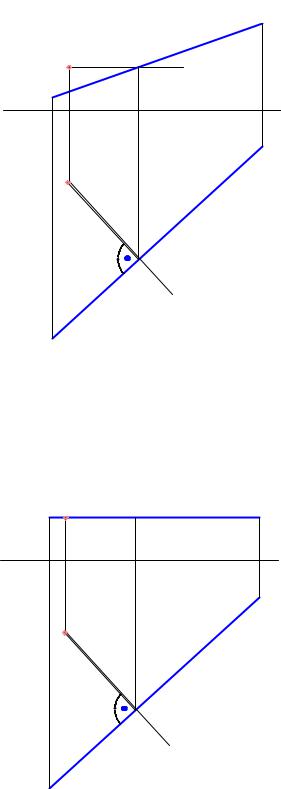
2.Точка и прямая задают плоскость, в которой прямая является линией ската. Тогда перпендикуляр, проведенный из точки на прямую окажется линией уровня и спроектируется на плоскость проекции в натуральную величину (Рис. 6.9).
61
|
C2 |
A2 |
K2 |
B2 |
|
x |
|
|
C1 |
|
A1 |
|
K1 |
B1 |
|
Рис. 6.9 Расстояние от точки до прямой. Случай 2
3.Точка и прямая образуют плоскость уровня. Тогда геометрические фигуры на плоскости, в том числе и перпендикуляр, опущенный из точки на прямую, будет проектироваться в натуральную величину.
A2 |
K2 |
C2 |
B2 |
|
|
x |
|
|
|
|
C1 |
A1 |
|
|
|
|
K1 |
B1 |
|
|
Рис. 6.10 Расстояние от точки до прямой. Случай 3
6.4.3Расстояние от точки до плоскости
Для того, чтобы отрезок, являющийся мерой расстояния между точкой и плоскостью, спроектировался в натуральную величину на плоскость проекции, необходимо, чтобы он был линией уровня по отношению к этой плоскости проекции. По определению такой
62

отрезок, это перпендикуляр, опущенный из точки на заданную плоскость. Перпендикуляр к плоскости будет линией уровня, если эта плоскость является проектирующей (Рис. 6.11).
|
C2 |
A2 |
K2 |
|
|
|
B2 |
|
D2 |
|
B1 |
|
K1 |
|
C1 |
A 1 |
|
|
D1 |
Рис. 6.11 Расстояние от точки до плоскости
6.4.4Расстояние между параллельными прямыми
При определении расстояния между параллельными прямыми могут быть рассмотрены четыре типовых случая:
1.Параллельные прямые образуют плоскость уровня. Тогда взаимный перпендикуляр между параллельными прямыми спроектируется на плоскость проекции без искажения (Рис. 6.12).
A |
M |
C |
N |
B |
D2 |
2 |
2 |
2 |
2 |
2 |
|
x |
|
|
|
|
|
|
|
|
|
B1 |
|
|
M1 |
|
|
|
D1 |
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
C1 |
N1 |
|
|
|
|
|
|
|
|
|
Рис. 6.12 Расстояние между |
|
|||
параллельными прямыми. Случай 1 |
|
||||
63
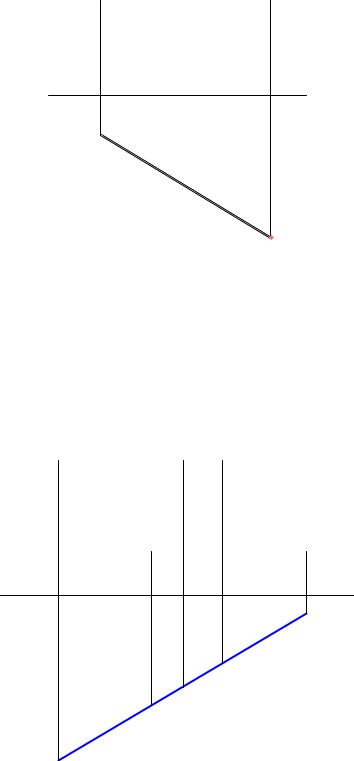
2.Параллельные прямые являются проектирующими линиями. Тогда перпендикуляр между ними будет линией уровня и спроектируется без искажения.
l |
|
m2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
x
A1 ≡l1 
B1 ≡m1
Рис. 6.13 Расстояние между параллельными прямыми. Случай 2
3.Параллельные прямые являются линиями уровня., принадлежащими проектирующей плоскости. Тогда перпендикуляр между ними является проектирующей прямой. На другой плоскости проекции проектирующая прямая отображается в натуральную величину (Рис. 6.14).
A2 |
|
M2 |
|
B2 |
|
|
|
|
|
|
|
|
|
|
C2 |
N2 |
D2 |
|
||||
|
|
|
|
|
|
|
|
|
D1
|
|
|
|
|
B1 |
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
≡N1 |
|
|
|
|
|
|
|||
A1
Рис. 6.14 Расстояние между параллельными прямыми. Случай 3

4.Параллельные прямые образуют плоскость, в которой они являются линиями ската. Тогда перпендикуляр между ними будет на ПП изображаться как перпендикуляр между проекциями этих прямых. Он будет являться линией уровня, проекция которой не искажается (Рис. 6.15).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M2 |
|
|
|
|
N2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
m2 |
|
|||||
x |
|
||||||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
l1 |
|
|
|
|
|
|
|||||
N1
m1
Рис. 6.15 Расстояние между параллельными прямыми. Случай 4
6.4.5Расстояние между скрещивающимися прямыми
При определении расстояния между скрещивающимися прямыми могут быть рассмотрены два типовых случая:
1.Мерой расстояния между скрещивающимися прямыми является их общий перпендикуляр. Этот перпендикуляр будет изображаться на ПП в натуральную величину, если он является линией уровня. Это возможно тогда, когда одна из скрещивающихся прямых является проектирующей прямой
(Рис. 6.16).
65

m2
M2
N2
l2
x
l1
m1 ≡N1
Рис. 6.16 Расстояние между скрещивающимися прямыми. Случай 1
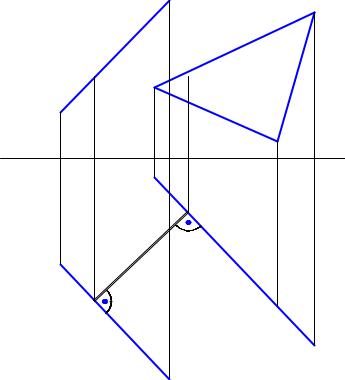
2.Общий перпендикуляр между двумя скрещивающимися прямыми окажется линией уровня, если две параллельные плоскости, в каждой из которых лежит одна из скрещивающихся прямых, будут проектирующими плоскостями
(Рис. 6.17).
|
|
|
|
|
|
|
B2 |
|
|
|
D2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
N2 |
|
|
A2 |
|
|
|
|
|
|
E2 |
||||
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|||||||
C1
N1
A1
E1
M1
D1
B1
Рис. 6.17 Расстояние между скрещивающимися прямыми. Случай 2
66
6.4.6Расстояние между прямой и плоскостью
Расстояние между прямой и плоскостью имеет геометрический смысл, только если прямая параллельна плоскости. Перпендикуляр, опущенный из любой точки прямой на плоскость, будет линией уровня, если заданная плоскость является проектирующей (Рис. 6.18).
|
|
|
|
|
|
|
B2 |
|
|
|
|
|
D2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
A2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
E2 |
|
C1
N1
A1
E1
M1
D1
B1
Рис. 6.18 Расстояние между прямой и плоскостью
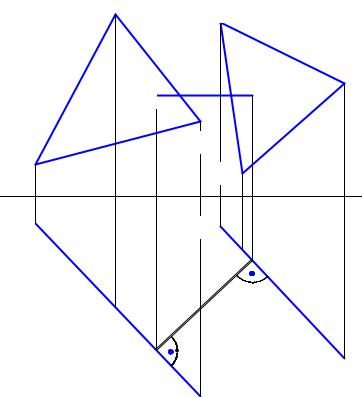
6.4.7Расстояние между двумя параллельными плоскостями
Перпендикуляр между двумя параллельными плоскостями, являющийся мерой расстояния между ними, буде линией уровня, проектирующейся в натуральную величину, если заданные плоскости проектирующие (Рис. 6.19).
67
B2 |
D2 |
|
|
M2 |
|
N |
E2 |
|
|
2 |
|
A2 |
C2 |
|
|
F2 |
|
|
|
x |
|
|
|
A1 |
D1 |
|
|
|
F1 |
N1 |
|
B1 |
|
|
|
M1 |
|
|
E1 |
C1 |
|
|
|
|
|
|
|
Рис. 6.19 Расстояние между параллельными плоскостями |
|||
68
Тема 7 Методы преобразования комплексного чертежа. Преобразование системы проектирования. Способ замены плоскостей проекций. Четыре основных позиционных задачи.
7.1Метод преобразования проекций. Цель и суть.
В реальности геометрические фигуры могут занимать разное положение, чаще общее, что затрудняет решение метрических и позиционных задач. Цель метода преобразования проекций – так изменить систему проектирования фигуры, чтобы фигура в новой системе заняла частное положение такое, при котором простым измерение могут быть получены метрические параметры фигур, или можно сразу понять взаимное положение фигур.
Изменение системы проектирования может быть реализовано двумя основными способами:
1.Замена плоскостей проекций. При этом способе положение объекта проектирования остается неизменным; изменяется положение плоскостей проекций.
2.Вращение, совмещение или плоскопараллельное перемещение фигур. При реализации этой группы способов система плоскостей проекций остается неизменной, изменяется положение фигур относительно нее.
7.2Способ замены ПП.
П2 |
|
|
|
Рассмотрим |
в |
системе |
||
|
|
|
плоскостей проекций П1/П2 |
|||||
|
|
|
|
|||||
|
А2 |
|
|
точку А. Ее проекции в этой |
||||
|
|
А3 |
|
системе А1 и |
А2. |
Введем |
||
|
А4 |
|
новую плоскость проекций |
|||||
х12 |
П4 |
|
П3 |
П4 П1. Точка А будет в |
||||
|
|
|
|
этой |
плоскости |
иметь |
||
|
А1 |
|
|
проекцию А4 (Рис. 7.1). Так |
||||
|
|
|
|
как |
высота |
точки |
не |
|
|
П1 |
А4 |
|
изменилась, |
отстояние |
|||
|
|
|
проекции А4 точки A на П4 |
|||||
|
|
П4 |
|
от плоскости П1 будет такое |
||||
|
|
|
|
же, как на плоскости П2. |
|
|||
|
Рис. 7.1 Замена П2 на П4 |
|
|
|
|
|
|
|
69
