∙Косая плоскость. Обе направляющие скрещивающиеся прямые (Рис. 13.18).
Рис. 13.18 Косая плоскость
∙ Плоскость. Направляющие параллельны или пересекаются.
Группа В2. Линейчатые поверхности с одной направляющей Торсы. Направляющая таких поверхностей называется ребром возврата (все три направляющие совпадают с ребром возврата) (Рис. 13.19).
Поверхность образована движением прямой направляющей, в каждой точке касательной кривой направляющей.
Рис. 13.19 Торс
146
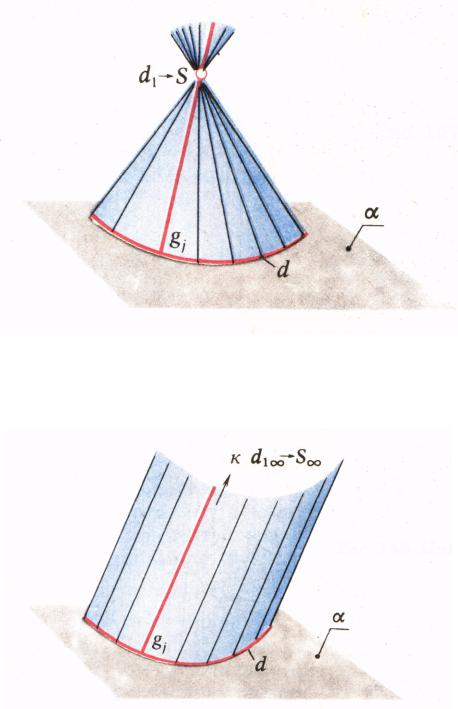
Особое свойство торсов – разворачиваемость на плоскость без складок и разрывов.
Если в частном случае ребро возврата выродилось в точку – получается коническая поверхность (Рис. 13.20).
Рис. 13.20 Торс с вырожденной в точку направляющей - конус
Если точка вырождения ребра возврата является несобственной точкой – получается цилиндрическая поверхность (Рис. 13.21).
Рис. 13.21 Торс с несобственной вырожденной точкой - цилиндр
Если ребро возврата – плоская кривая, получается плоскость.
13.8Поверхности параллельного переноса (подкласс1)
Образованы поступательным перемещение плоской линии, остающейся все время параллельными между собой, т.е. имеют
147
плоскость параллелизма, или, иначе, лежат в параллельных плоскостях (Рис. 13.22).
Рис. 13.22 Поверхность параллельного пеноса образующей
13.9Поверхности вращения (подкласс 2)
Образованы вращением кривой образующей вокруг неподвижной оси
(Рис. 13.23).
Рис. 13.23 Элемент тела вращения
148
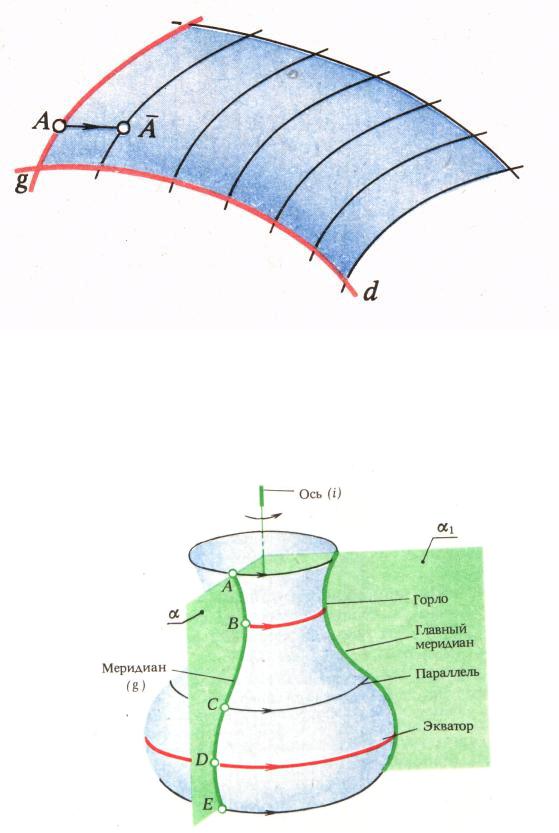
Меридиан – кривая, полученная при рассечении поверхности плоскостью, проходящей через ось поверхности вращения.
Параллель – траектория движения точки на образующей.
При вращении окружности вокруг оси в ее плоскости можно получить сферу, если ось вращения проходит через центр окружности, и тор, когда ось смещена от центра окружности.
При вращении эллипса вокруг его осей может быть получен сжатый (вокруг малого диаметра) и растянутый (вокруг большого диаметра)
эллипсоид.
При вращении гиперболы
∙вокруг ее действительной оси получается двуполостный гиперболоид вращения.
∙вокруг ее мнимой оси получается однополостный гиперболоид вращения. Иначе однополостный гиперболоид получается при вращении прямой образующей вокруг скрещивающейся с ней оси.
При вращении параболы вокруг ее оси получается параболоид вращения.
13.10Винтовые поверхности (подкласс 3)
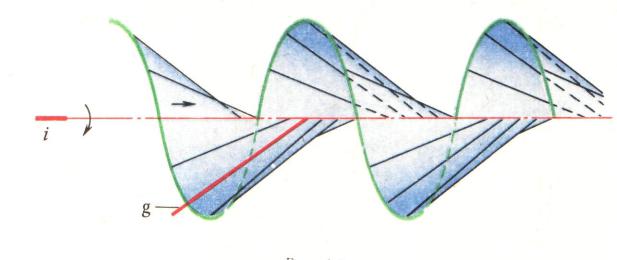
Образуются при одновременном вращении образующей вокруг оси и поступательном перемещении точки на образующей вдоль оси. Направляющая – винтовая линия (Рис. 13.24).
Рис. 13.24 Винтовая поверхность
Направляющая винтовая линия постоянного шага на поверхности прямого кругового цилиндра называется гелисой.
149