9.3Сечения тел вращения плоскостями
Если секущая плоскость занимает частное положение, построение фигуры сечения тела вращения этой плоскостью, как правило, не составляет труда. Если же плоскость занимает общее положение, заменой плоскостей проекций можно добиться частного положения этой секущей плоскости.
Для построения натурального вида фигуры сечения используется один из способов перемены системы проектирования (перемена ПП, вращение фигуры вокруг проектирующей оси или вокруг линии уровня, совмещение плоскости сечения с ПП), либо комбинация этих способов. Для построения разверток тел вращения, если необходимые геометрические элементы не отображаются на ПП в натуральную величину, используются методы перемены системы проектирования для получения нужной натуральной величины геометрических элементов, например, метод вращения относительно проектирующей оси или линии уровня.
Пример 9.1: Построить проекции и натуральный вид сечения прямого кругового цилиндра фронтально-проектирующей плоскостью и развертку усеченной части цилиндра (Рис. 9.9).
Фронтальная проекция линии сечения совпадает со следом секущей плоскости Σ и является отрезком прямой А2Е2.
Горизонтальная проекция линии сечения совпадает с окружностью основания цилиндра. Секущая плоскость проходит через основание. Отрезок KL линии сечения основания плоскостью хорда основания, на горизонтальной плоскости проекции перпендикулярен оси х.
Действительный вид сечения – эллипс, большая ось которого равна отрезку между прямой в секущей плоскости между крайними (очерковыми) образующими цилиндра. Построение действительного вида сечения способом замены плоскости проекции плоскостью, параллельной секущей (совпадающей с секущей).
Для построения развертки окружность основания разбивается на равные части (8, 12). Через точки разбиения на фронтальную проекцию цилиндра наносятся линии связи, дающие образующие цилиндра. Вычисляется длина окружности в основании цилиндра.
L=2πR
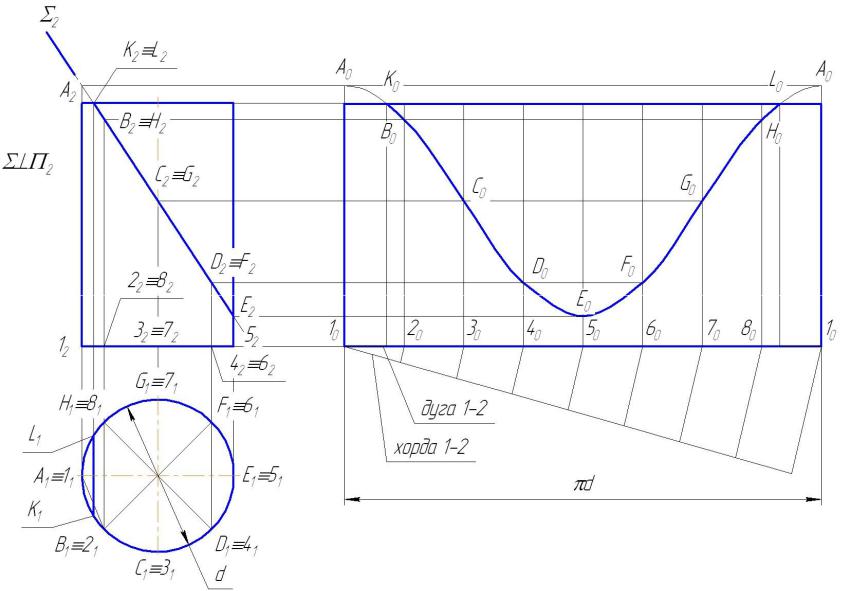
Рис. 9.9 Построение линии сечения цилиндра
Длина окружности откладывается на прямой. Полученный отрезок является разверткой основания. Он делится на части, число которых равно числу разбиений основания цилиндра. Из полученных на прямой точек восстанавливаются перпендикуляры. На перпендикулярах откладываются отрезки, равные отстоянию точек сечения цилиндра плоскостью на соответствующих образующих. Полученные точки соединяются плавной кривой, которая будет участком синусоиды.
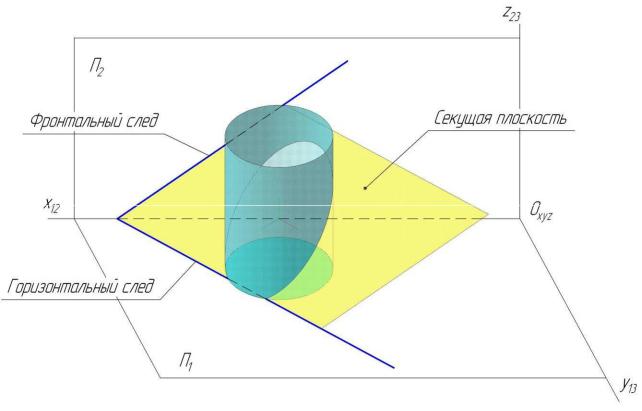
Пример 9.2: Построить проекции и натуральный вид сечения прямого кругового цилиндра плоскостью общего положения. Плоскость задана следами (Рис. 9.10; Рис. 9.11).
Рис. 9.10 Сечение цилиндра плоскостью общего положения
Для построения линии сечения используются:
∙Для двух точек линии сечения, расположенных на концах большой диагонали эллипса-сечения – вспомогательная горизонтально-проектирующая плоскость, проходящая через центр цилиндра по линии ската секущей плоскости. Линия ската секущей плоскости, пересекающая ось цилиндра совпадает с большой осью эллипса сечения цилиндра. Горизонтально-проектирующая вспомогательная плоскость пересекает цилиндр по образующим.
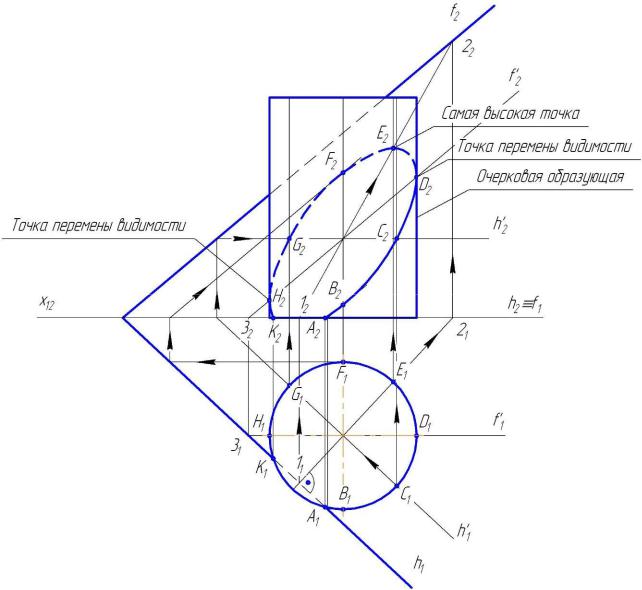
∙Для двух точек линии сечения, расположенных на концах малой диагонали эллипса-сечения используется вспомогательная горизонтально-проектирующая плоскость, проходящая через центр цилиндра;
∙Для других точек вспомогательные горизонтальнопроектирующие плоскости, перпендикулярные линии ската
(см. Рис. 9.11).
Рис. 9.11 Построение фигуры сечения цилиндра плоскостью общего положения. Обозначены только некоторые, наиболее важные характерные точки.
Для построения натурального вида фигуры сечения можно использовать, например, способ совмещения секущей плоскости с горизонтальной плоскостью проекции (Рис. 9.12).
102