
- •В. Н. Бєловодський Вісім лекцій по чисельних методах
- •7.080407 «Комп'ютерний еколого-економічний моніторинг»)
- •Лекція 1.Елементи теорії погрішностей
- •.Типи й джерела погрішностей
- •1.2.Абсолютні й відносні погрішності наближених чисел
- •1.3. Погрішності виконання арифметичних операцій
- •.Погрішність обчислення функції
- •1.5.Запис наближених чисел
- •1.6.Правила дій над наближеними числами
- •1.7.Погрішності при машинному поданні чисел
- •1.8. Варіанти індивідуальних завдань
- •Лекція 2. Інтерполяція функцій
- •2.1. Постановка задачі
- •2.2. Алгебраїчна інтерполяція, існування й одиничність інтерполяційного багаточлена
- •2.3. Інтерполяційний багаточлен Лагранжа
- •2.4. Кінцеві й розділені різниці
- •2.5. Інтерполяційний багаточлен Ньютона
- •2.6. Порівняльний аналіз інтерполяційних багаточленів
- •2.7. Погрішності інтерполяційних формул
- •2.8. Інтерполяційні формули для рівновіддалених вузлів
- •2.9. Сплайн - інтерполяція
- •2.10. Варіанти індивідуальних завдань
- •Лекція 3. Методи рішення систем лінійних алгебраїчних рівнянь
- •3.1. Попередні зауваження
- •3.2. Точні методи рішення
- •3.3. Наближені методи рішення
- •3.4. Збіжність і погрішність наближених методів
- •3.6. Варіанти індивідуальних завдань
- •Лекція 4. Вирішення нелінійних рівнянь
- •4.1. Попередні зауваження
- •4.2. Методи, засновані на алгебраїчній інтерполяції
- •4.3. Метод послідовних наближень
- •4.4. Завдання
- •Лекція 5. Рішення систем нелінійних рівнянь
- •Метод ітерацій
- •Метод Ньютона
- •5.3. Порівняльний аналіз методів
- •5.4. Завдання
- •Вимоги до програми
- •Вимоги до звіту
- •6.1. Вступні зауваження
- •6.2. Формули Ньютона-Котеса
- •6.3. Найпростіші квадратурні правила
- •6.4. Погрішності квадратурних формул
- •6.5. Поняття про методи Монте-Карло
- •6.6. Завдання
- •Варіанти завдань
- •Лекція 7. Методи рішення звичайних диференціальних рівнянь
- •Вступні зауваження
- •Аналітичні методи
- •Чисельні методи рішення. Правило Рунге
- •Завдання
- •Лекція 8. Основи спектрального аналізу
- •Елементи загальної теорії
- •Дискретна форма рядів Фур'є
- •8.4. Завдання
Лекція 2. Інтерполяція функцій
У якій формулюється постановка задачі й проводиться побудова основних інтерполяційних багаточленів. Коротко описана методика побудови кубічних сплайнов.
2.1. Постановка задачі
У загальному випадку задача апроксимації формулюється в такий спосіб.
|
У
точках
х0,
х1,
…хn,
називаних
вузловими,
дані значення функції
|
У теорії інтерполяції ця задача вирішується в такий спосіб. У попередньо обраному класі функцій будується така функція P(x), вона називається що інтерполює, котра у вузлових точках задовольняє вихідним даним, після чого шукане значення f(x) приймається рівним P(x).
Залежно від обраного класу функцій методика побудови функції, що інтерполює, має свої особливості. Нижче розглянемо випадки, що коли інтерполює функція є алгебраїчним багаточленом, така інтерполяція називається алгебраїчної, або представленої у вигляді сукупності багаточленів ( сплайн-інтерполяція).
2.2. Алгебраїчна інтерполяція, існування й одиничність інтерполяційного багаточлена
Як уже відзначено вище, при алгебраїчній інтерполяції функція, що інтерполює, шукається у вигляді багаточлена, він називається інтерполяційним багаточленом. Задача його знаходження формулюється в такий спосіб.
|
Дано
значення
|
Виявляється, що дана задача розв'язна й має єдине рішення. Дійсно, нехай
![]() ,
,
– шуканий
багаточлен,
![]() –
невідомі коефіцієнти.
–
невідомі коефіцієнти.
Тоді
для визначення коефіцієнтів
![]() маємо лінійну систему рівнянь
маємо лінійну систему рівнянь
|
|
Головним
визначником системи (2.1), позначимо його
через
![]() ,
є визначник
,
є визначник
 ,
,
який називається визначником Вандермонда.
Індукцією по n можна показати, що
![]() .
.
Очевидно,
що при
![]() значення
значення![]() .
Отже, система (2.1) має єдине рішення й,
отже, існує єдиний інтерполяційний
багаточлен.
.
Отже, система (2.1) має єдине рішення й,
отже, існує єдиний інтерполяційний
багаточлен.
2.3. Інтерполяційний багаточлен Лагранжа
Він шукається у вигляді
|
|
де
коефіцієнти
![]() є багаточленами й задовольняють умовам
є багаточленами й задовольняють умовам
 .
.
Виявляється,
що цих вимог досить для однозначного
визначення
![]() .
Дійсно, багаточлен
.
Дійсно, багаточлен![]() звертається в нуль у вузлових точках
звертається в нуль у вузлових точках![]() .
Отже, він має розкладання
.
Отже, він має розкладання
![]() .
.
Покладемо
тепер
![]() .
Тоді
.
Тоді
![]() ,
,
звідки
![]() .
.
З метою скорочення запису введемо функцію
|
|
тоді
![]() ,
,
![]()
і багаточлен (2.2) приймає вид
|
|
де ω(x) описується вираженням (2.3). Багаточлен (2.4) і називається інтерполяційним багаточленом Лагранжа.
2.4. Кінцеві й розділені різниці
Кінцеві й розділені різниці відіграють особливу роль у теорії інтерполяції. Вони використовуються як для формування нових інтерполяційних формул, так і для оцінки погрішності інтерполяції.
Нехай
дана таблиця
![]() значень функції
значень функції![]() .Кінцевою
різницею першого порядку в точцi xi
(позначається
символом
.Кінцевою
різницею першого порядку в точцi xi
(позначається
символом
![]() ),
називається вираження
),
називається вираження
![]() ,
,
другого
порядку,
позначається
![]() ,
– вираження
,
– вираження
![]() ,
,
k-го порядку, –
|
|
Так,
наприклад,
![]() ,
,![]() ,
,![]()
Розділеною
різницею першого порядку в точках
![]() ,
,![]() , позначається
, позначається![]() , називається вираження
, називається вираження
![]() ,
,
другого
порядку в точках
![]() ,
,![]() ,
,![]() ,
позначається
,
позначається![]() ,
– вираження
,
– вираження
![]() ,
,
k-го
порядку в точках
![]() ,
,![]() ,
,![]() ,
– вираження
,
– вираження
 .
.
Так, наприклад,
![]() ,
,
![]() ,
,
![]() .
.
Одержимо деякі корисні для подальшого співвідношення, пов'язані з розділеними різницями.
Виразимо
![]() через значення функції у вузлових
точках. Так, безпосередньо з визначення
треба
через значення функції у вузлових
точках. Так, безпосередньо з визначення
треба
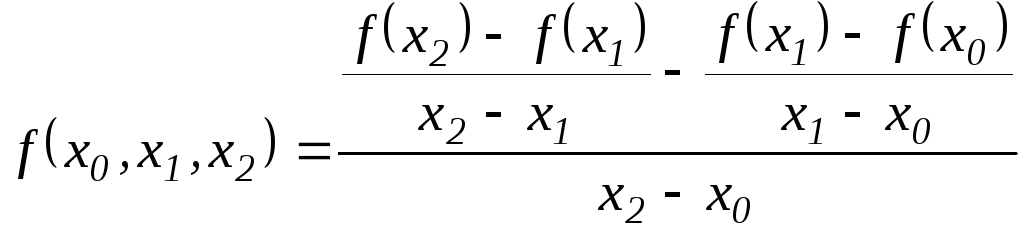 ,
,
і, після очевидних перетворень,
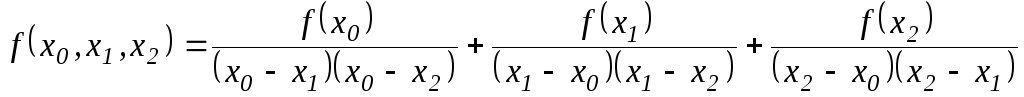 .
.
Продовжуючи, далі, по індукції, одержимо
 .
.
Або, для
скорочення запису, використовуючи
функцію
![]() (2.3),
(2.3),
|
|
|
Зауваження.
Якщо в
|
Так, наприклад
![]() ,
,
![]() і т.д.
і т.д.
Одержимо тепер друге корисне співвідношення.
Виразимо
![]() через розділені різниці. Так, безпосередньо
з визначення треба
через розділені різниці. Так, безпосередньо
з визначення треба
![]()
Додаючи
тепер до правої частини
![]() після очевидних перетворень одержимо
після очевидних перетворень одержимо
![]() .
.
Міркуючи далі по індукції по m прийдемо до шуканого співвідношення
|
|
Якщо
тепер змінити нумерацію точок і позначити
![]() через
через![]() ,
,![]() через
через![]() і т.д., то співвідношення (2.6) з урахуваннямсиметричності
розподілених різниць
приймає
вид
і т.д., то співвідношення (2.6) з урахуваннямсиметричності
розподілених різниць
приймає
вид
|
|

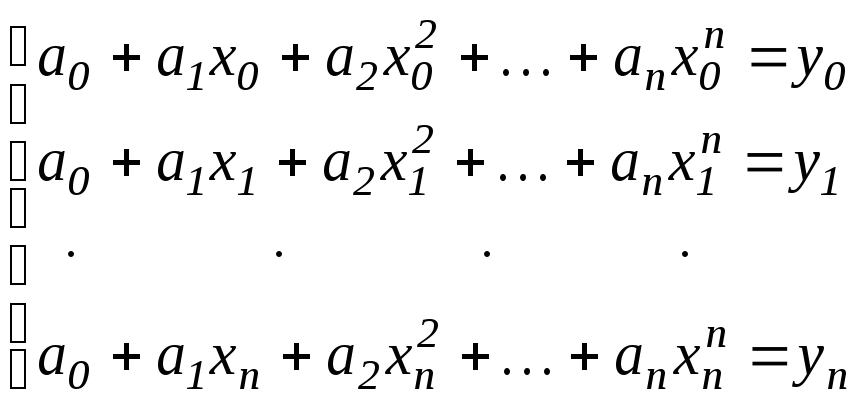 (2.1)
(2.1) (2.5)
(2.5)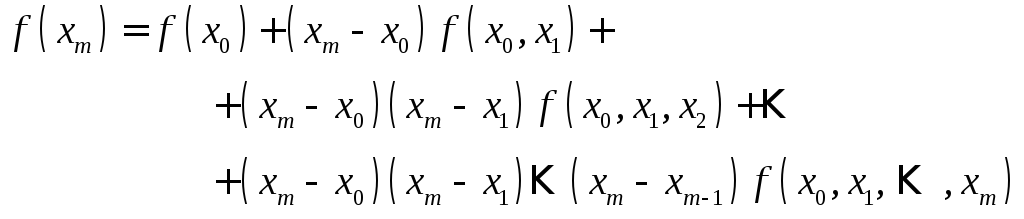 (2.6)
(2.6) (2.61)
(2.61)