- •В. Н. Бєловодський Вісім лекцій по чисельних методах
- •7.080407 «Комп'ютерний еколого-економічний моніторинг»)
- •Лекція 1.Елементи теорії погрішностей
- •.Типи й джерела погрішностей
- •1.2.Абсолютні й відносні погрішності наближених чисел
- •1.3. Погрішності виконання арифметичних операцій
- •.Погрішність обчислення функції
- •1.5.Запис наближених чисел
- •1.6.Правила дій над наближеними числами
- •1.7.Погрішності при машинному поданні чисел
- •1.8. Варіанти індивідуальних завдань
- •Лекція 2. Інтерполяція функцій
- •2.1. Постановка задачі
- •2.2. Алгебраїчна інтерполяція, існування й одиничність інтерполяційного багаточлена
- •2.3. Інтерполяційний багаточлен Лагранжа
- •2.4. Кінцеві й розділені різниці
- •2.5. Інтерполяційний багаточлен Ньютона
- •2.6. Порівняльний аналіз інтерполяційних багаточленів
- •2.7. Погрішності інтерполяційних формул
- •2.8. Інтерполяційні формули для рівновіддалених вузлів
- •2.9. Сплайн - інтерполяція
- •2.10. Варіанти індивідуальних завдань
- •Лекція 3. Методи рішення систем лінійних алгебраїчних рівнянь
- •3.1. Попередні зауваження
- •3.2. Точні методи рішення
- •3.3. Наближені методи рішення
- •3.4. Збіжність і погрішність наближених методів
- •3.6. Варіанти індивідуальних завдань
- •Лекція 4. Вирішення нелінійних рівнянь
- •4.1. Попередні зауваження
- •4.2. Методи, засновані на алгебраїчній інтерполяції
- •4.3. Метод послідовних наближень
- •4.4. Завдання
- •Лекція 5. Рішення систем нелінійних рівнянь
- •Метод ітерацій
- •Метод Ньютона
- •5.3. Порівняльний аналіз методів
- •5.4. Завдання
- •Вимоги до програми
- •Вимоги до звіту
- •6.1. Вступні зауваження
- •6.2. Формули Ньютона-Котеса
- •6.3. Найпростіші квадратурні правила
- •6.4. Погрішності квадратурних формул
- •6.5. Поняття про методи Монте-Карло
- •6.6. Завдання
- •Варіанти завдань
- •Лекція 7. Методи рішення звичайних диференціальних рівнянь
- •Вступні зауваження
- •Аналітичні методи
- •Чисельні методи рішення. Правило Рунге
- •Завдання
- •Лекція 8. Основи спектрального аналізу
- •Елементи загальної теорії
- •Дискретна форма рядів Фур'є
- •8.4. Завдання
2.8. Інтерполяційні формули для рівновіддалених вузлів
Розглянемо
формулу Ньютона (2.7) і припустимо, що
вузли є рівновіддаленими, а саме,
![]() ,
де
,
де![]() .
Зробимо в ній заміну
.
Зробимо в ній заміну![]() й урахувавши (2.11), одержимо
й урахувавши (2.11), одержимо
|
|
Це і є багаточлен Ньютона для рівновіддалених вузлів, а погрішність інтерполяції при його використанні оцінюється вираженням (2.12).
Відзначимо,
що зі збільшенням порядку значення
кінцевої різниці
![]() убуває. Тому нерідко необхідна точність
обчислення значення функції досягається
при меншій кількості доданків, тобто
при меншому числі використаних вузлових
точок. У зв'язку із цим, залежно від
розташування значенняx
серед масиву значень x0
,
x1
,
…
xn
на основі (2.7) формують окремі формули,
використовувані для інтерполяції на
початку, кінці й середині таблиці.
Розглянемо ці випадки.
убуває. Тому нерідко необхідна точність
обчислення значення функції досягається
при меншій кількості доданків, тобто
при меншому числі використаних вузлових
точок. У зв'язку із цим, залежно від
розташування значенняx
серед масиву значень x0
,
x1
,
…
xn
на основі (2.7) формують окремі формули,
використовувані для інтерполяції на
початку, кінці й середині таблиці.
Розглянемо ці випадки.
Нехай значення x близько до x0 . Тоді вибираючи для інтерполяції вузлові точки x0 , x0 + h, x0 +m h одержимо
|
|
її погрішність, відповідно до (2.12)
|
|
Нехай
тепер значення x
близько до xn
, тобто до кінця таблиці. Тоді вибираючи
для інтерполяції вузли xn,
xn
– h,…,xn–mhі
зробивши заміну
![]()
![]()
![]() з (2.7) одержуємо
з (2.7) одержуємо
|
|
погрішність інтерполяції
|
|
Якщо
значення x
близько до деякому xk
,
розташованому в середній частині
таблиці, то для інтерполяції звичайно
використовують точки xk
, xk
+
h,
xk
-h,…,xk+mh,xk-mhВідповідний
інтерполяційний багаточлен також
виходить із (2.7) і після заміни
![]() приймаємо
приймаємо
|
|
його погрішність оцінюється вираженням.
|
|
Інтерполяційному багаточлену (2.16) можна додати більше симетричний вид. Так, розбиваючи непарні доданки, починаючи із третього, на два, і групуючи з парними, одержимо
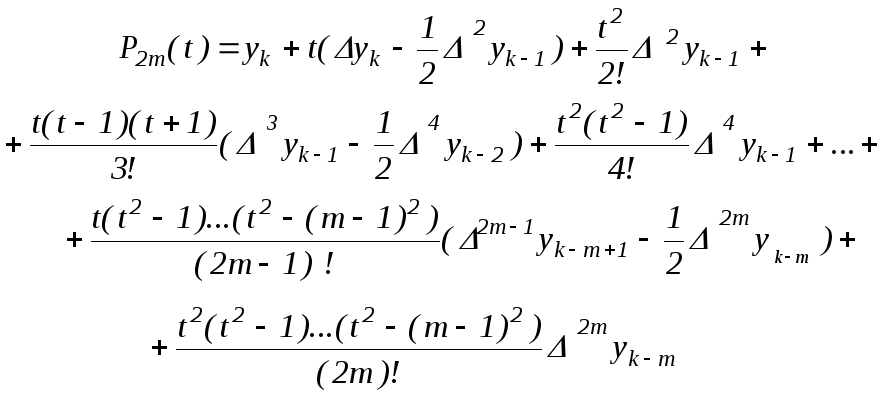
Представимо тепер різниці в дужках у вигляді
![]() ,
,
![]() і т.д., одержимо багаточлен,
і т.д., одержимо багаточлен,
який називається інтерполяційним багаточленом Ньютона – Стiрлiнга.
2.9. Сплайн - інтерполяція
Одним з недоліків розглянутих методів є високий ступінь інтерполяційного багаточлена, що не завжди є бажаним. Розбивка ж вихідного відрізка на часткові й побудова на них окремих інтерполяційних багаточленів приводить до того, що в точках стику багаточленів похідні розривнi. Цього недоліку позбавлені функції, що інтерполюють, побудовані на основі сплайнов.
|
Сплайном на відрізку [a, b] називається функція, безперервна на відрізку разом зі своїми похідними до заданого порядку включно, що на часткових проміжках цього відрізка описується різними алгебраїчними багаточленами.
|
Розглянемо методику побудови сплайна, заснованого на алгебраїчних багаточленах третього ступеня, тобто так звану, кубічну сплайн – інтерполяцію.
Як і
раніше, уважаємо заданої таблицю значень
функції
![]() в точкахa=x0
,
x1
,
x2
,
…,
xn
= b...
На кожному з відрізків [ xi-1
, x
i]
багаточлен Pi(x)
будемо
шукати у вигляді
в точкахa=x0
,
x1
,
x2
,
…,
xn
= b...
На кожному з відрізків [ xi-1
, x
i]
багаточлен Pi(x)
будемо
шукати у вигляді
![]()
Таким чином, загальне число багаточленів дорівнює n, а число невідомих коефіцієнтів,- 4n . Тому для їхнього визначення необхідно така ж кількість умов.
Зажадаємо, щоб кожний багаточлен у крайніх точках свого відрізка задовольняв умовам
![]() ,
,
![]() ,
,![]() ,
,
що дає 2n співвідношень. Далі, зажадаємо, щоб у внутрішніх вузлових точках перша й друга похідні функції, що інтерполює, були безперервними, тобто
![]() ,
,
![]() ,
,![]() .
.
Це дає ще 2( n-1) обмежень. Для одержання двох відсутніх можна додатково зажадати, що в крайніх точках відрізка функція, що інтерполює, мала нульову кривизну, тобто,
![]() ,
, ![]()
Таким чином, для визначення коефіцієнтів багаточленів маємо систему рівнянь.

![]() ,
,
яка
виявляється лінійною. У тому випадку,
коли вузлові точки є рівновіддаленими,
тобто
![]() ,
вона істотно спрощується й приймає вид
,
вона істотно спрощується й приймає вид
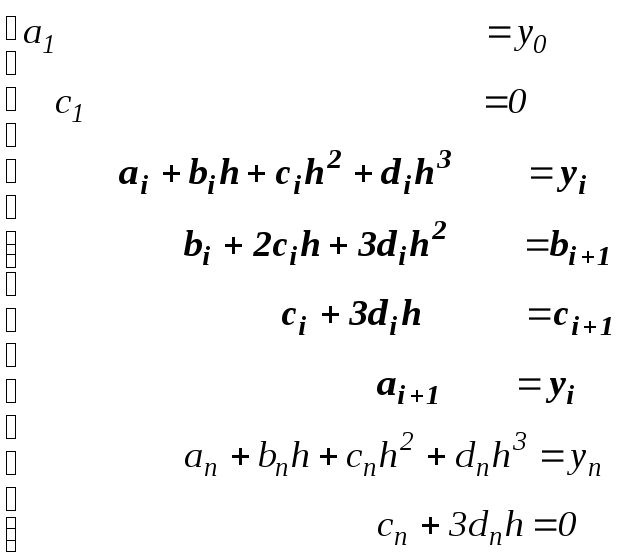
![]() .
.
Зокрема, для трьох рівновіддалених вузлів, тобто n=2 , маємо
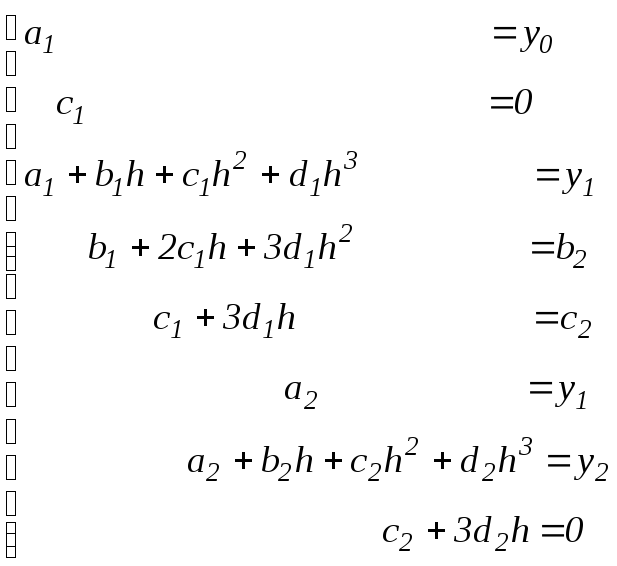
яка
легко вирішується в загальному виді.
Дійсно, з 1-го, 2-го, 5-го й 6-го рівнянь
треба
![]() ,
,![]() ,
,![]() і
і![]() ,
а частина, що залишилася, після традиційних
перетворень приводиться до трикутного
виду
,
а частина, що залишилася, після традиційних
перетворень приводиться до трикутного
виду
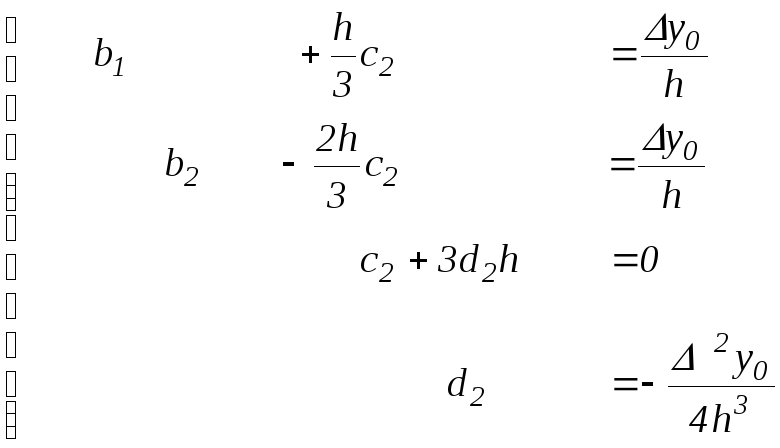 .
.

 (2.13)
(2.13)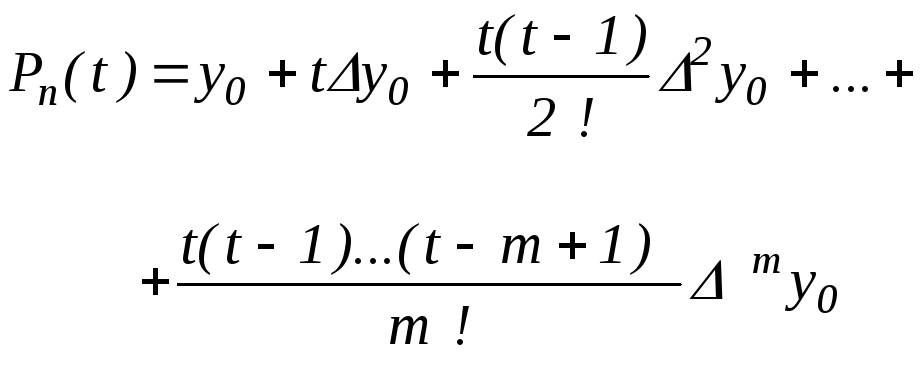 (2.14),
(2.14),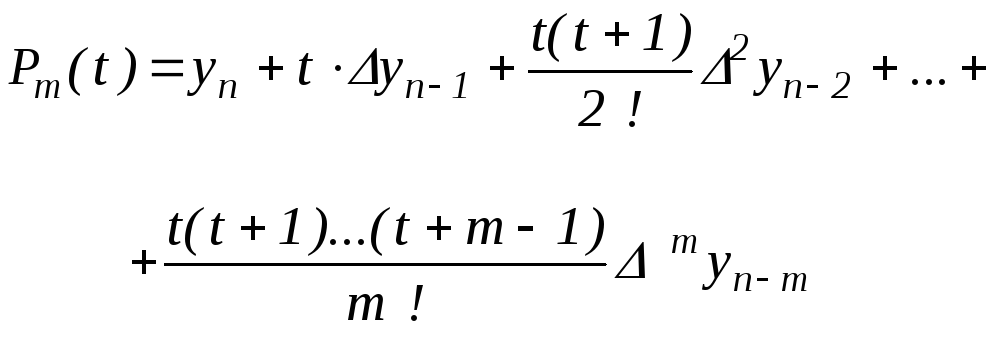 (2.15),
(2.15),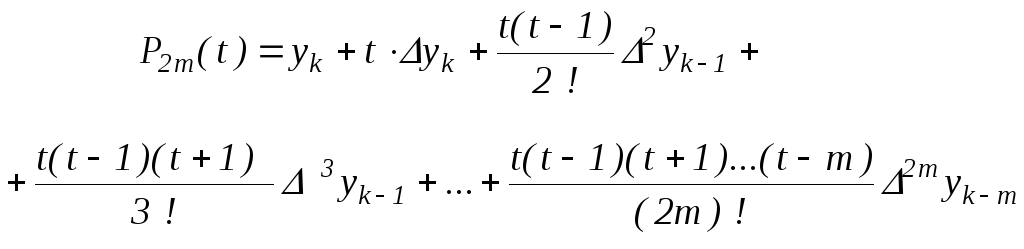 (2.16),
(2.16),