Лекція 1.Елементи теорії погрішностей

У якій розглядаються основні поняття теорії погрішностей, а також характер поширення погрішності при виконанні арифметичних операцій і обчисленні функції. Приводяться правила запису наближених чисел і практичні правила дії над ними. Відзначаються особливості машинного подання чисел.

1. .Типи й джерела погрішностей

Виникаючі при математичному моделюванні погрішності умовно ділять на три типи,- непереборну, погрішність апроксимації й обчислювальну. Джерелами першої з їх є неточності в складанні математичної моделі, а також у завданні вихідних даних. Обчислювач, як правило, не має змоги впливати на величину цієї погрішності, мабуть, тому вона так і називається,- непереборна. Джерелом погрішності апроксимації є заміна вихідної математичної моделі інший, більше зручної для дослідження. Такий перехід звичайно виробляється з метою спрощення або видозміни моделі, що скорочує, або відкриває шлях до одержання рішення. Погрішність, що виникає внаслідок помилок округлення, виробленого в процесі обчислень, називається обчислювальної.

Пояснимо це на прикладі.

Припустимо, що обчислення значення sinx вирішено проводити по формулі .

Тоді неточність у завданні значення x , якщо вона є, утворить непереборну погрішність. Величина sinx-f(x) представити собою погрішність апроксимації. А проведені в процесі обчислень округлення, обумовлять обчислювальну погрішність.

Метою даного розділу є розробка методів чисельного аналізу готових математичних моделей. Тому в першу чергу в поле зору попадають погрішність апроксимації й обчислювальна. Величина й особливості їхнього поводження в процесі обчислень ставляться до числа важливих показників, що характеризують якість обчислювальних схем.

1.2.Абсолютні й відносні погрішності наближених чисел

Ці поняття ставляться до числа базових у теорії погрішностей.

Позначимо через точне значення деякої величини, черезx ,- його наближене значення. Тоді різниця називаєтьсяпогрішністю наближеного числа x. При діях з наближеними числами звичайно відомо, що абсолютна величина погрішності не перевершує деякої величини, тобто

Величина являє собою оцінку абсолютної величини погрішності й називається граничноюабсолютною погрішністю наближеного числа x. Природно, у якості , за наявною інформацією, вибирають найменшу величину, що задовольняє зазначеній умові. Відзначимо, що при наявностіможе бути встановлений і діапазон розташування точного значенняx. Дійсно, тому що , то.

Відношення

являє собою відносну погрішність наближеного числа x. Алі тому що , загалом кажучи, не відома, ті в якості відносної приймають верхню оцінкумодуля цього відношення. Тобто. величина, така, що

називається граничною відносною погрішністю числа x. Очевидно, що й.

Іноді величину виражають і у відсотках. Помітимо, що при наявностітакож може бути встановлений діапазон розташування точного значення. Дійсно, тому що

,

ті .

1.3. Погрішності виконання арифметичних операцій

Установимо характер розвитку погрішностей при виконанні арифметичних операцій. Позначимо , де- один із символів ± , ∙, ÷ . Будемо вважати відомими погрішності операндов ∆(x), ∆(y), δ(x), δ(y) і позначимо через ,,їхні точні значення.

Додавання. У цьому випадку , де- числа одного знака. Тоді справедливі наступні оцінки

.

Таким чином, маємо

, (1.1)

т.е. абсолютна погрішність суми двох наближених чисел дорівнює сумі абсолютних погрішностей доданків.

Отриманий результат очевидним образом узагальнюється й на довільне число доданків.

Далі, тому що

,

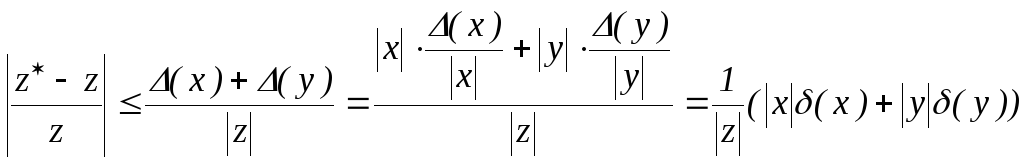тобто

. (1.2)

Вирахування. У цьому випадку , де значення- числа одного знака. Також, як і у випадку додавання, отут

т.е.

, (1.3)

що збігається з (1.1).

У такий же спосіб,

,

і

, (1.4)

що збігається з (1.2).

Аналіз виражень (1.3), (1.4) показує, що при вирахуванні близьких чисел , тобто при z > 0, погрішність ?(z) може перевищувати результат, а величина ?(z)> ?. Тому при обчисленнях необхідно уникати вирахування близьких чисел.

Множення. У цьому випадку . Тоді

Далі, з огляду на

,

маємо

.

У такий спосіб

, (1.5)

а

. (1.6)

Відзначимо, якщо або‹‹ 1, ті

. (1.61)

Ділення. У цьому випадку . Тоді

З огляду на, що , маємо

.

У такий спосіб

, (1.7)

Отут, природно, передбачається, що .

Далі, тому що

,

ті

(1.8)

Якщо ‹‹ 1, ті

,

що збігається з (1.61).

Зведемо в таблицю отримані результати.

Таблиця 1.1. Погрішності виконання арифметичних операцій

№	Операція			Примітки
1.	z=x+ y
2.	z=x - y
3.	z=x y			, якщо або ‹‹1
4.				, якщо ‹‹1