2.5. Інтерполяційний багаточлен Ньютона

За аналогією з (2.6) розглянемо багаточлен ступеня n .

(2.7)

Визначимо його значення у вузлових точках. Так, безпосередньо з (2.7) маємо

Далі,

,

але, з урахуванням (2.6) при це рівняється.

Т.о.

Аналогічним образом одержуємо, що

Таким чином, багаточлен (2.7) приймає задані значення в заданих точках і, отже, є інтерполяційним. Він і називається інтерполяційним багаточленом Ньютона. Помітимо, що в силу одиничності (п. 2.2) розходження між інтерполяційними багаточленами Лагранжа й Ньютона чисто зовнішні.

2.6. Порівняльний аналіз інтерполяційних багаточленів

Зовнішні розходження інтерполяційних багаточленів спричиняють ряд особливостей, що впливають на зручність їхнього застосування. Відзначимо деякі з них. Насамперед укажемо, що загальним є те, що нумерація точок абсолютно довільна й ніяк не пов'язана з їхніми числовими значеннями.

До числа достоїнств багаточленів Лагранжа можна віднести ту обставину, що при фіксованих x_i, x і зміні y_i коефіцієнти не перераховуються. До числа особливостей, – роль коефіцієнтів. Їх можна розглядати, як свого роду, вагові коефіцієнти приy_i і по величині можна судити про значимість можливих змінy_i. Ця властивість виявляється корисним при теоретичному аналізі.

Як достоїнства багаточлена Ньютона можна відзначити, що при додаванні додаткових вузлових точок відсутня необхідність перерахування коефіцієнтів. У силу відзначеної довільності нумерації вузлових точок до вже наявного багаточлена просто додаються додаткові доданки. Багаточлен Лагранжа такоi особливістi не має.

2.7. Погрішності інтерполяційних формул

Нижче зупинимося лише на основних елементах методики оцінки погрішності інтерполяційних формул, постараючись зберегти її логічну схему.

Нехай y=f(x), - дана функція, а P_n(x)- її інтерполяційний багаточлен. Тоді погрішність R_n(x) інтерполяції функції в точцi х дорівнює

R_n(x)=f(x) – P_n(x),

звідки

f(x)=P_n(x)+R_n(x) (2.8)

Додамо тепер точку x до заданих вузлових точок і розглянемо інтерполяційний багаточлен P_n+1(z) у формі Ньютона, побудований уже по (n+2) точкам х₀, х₁…х_{n ,} x . Його значення в тоці x дорівнює:

P_n+1(x)=f(x)+( x-x₀)f(x₀, х₁)+...+( х-х₀)...( х-хn)f(x₀,...х_n, х)

Але, по побудові, , а першідоданків правої частини являють собою. Таким чином,

.

Порівнюючи тепер це співвідношення з (2.8) ,одержуємо

(2.9)

Це і є одна з форм подання погрішності апроксимації. Її недоліком є та обставина, що для обчислення необхідне значення, що невідомо. Як вихід з такого положення залишається взяти лише його наближене значення, тобто, однак у цьому випадку співвідношення (2.9) стає вже наближеним.

Якщо ж припустити, що функціядосить гладка й має безперервні похідні до-го порядку включно, то з формули

,

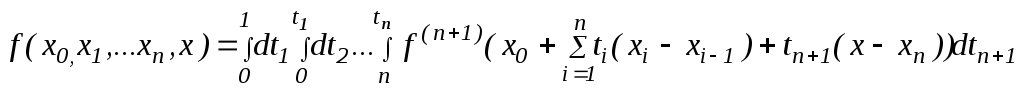справедливість якої треба по індукції, по теоремі про середній випливає співвідношення

,

де Тоді (2.9) приймає вид

(2.10)

Недоліком цього співвідношення є те, що невідомо значення . Однак, якщо відомо вид функції,те корисної може виявитися оцінка

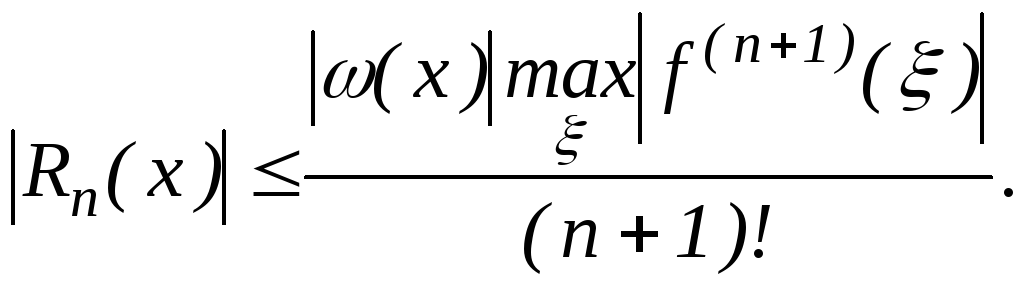
У тому випадку, коли вузлові точки рівновіддалені й ,, те по індукції можна показати, що

(2.11)

Якщо до них додати точку не змінює характер розташування вузлів, то формула залишається справедливої й для розділеної різниці наступного порядку. Т.е.

.

У противному випадку, остання рівність стає наближеним, і зробивши в заміну, одержимо

(2.12)