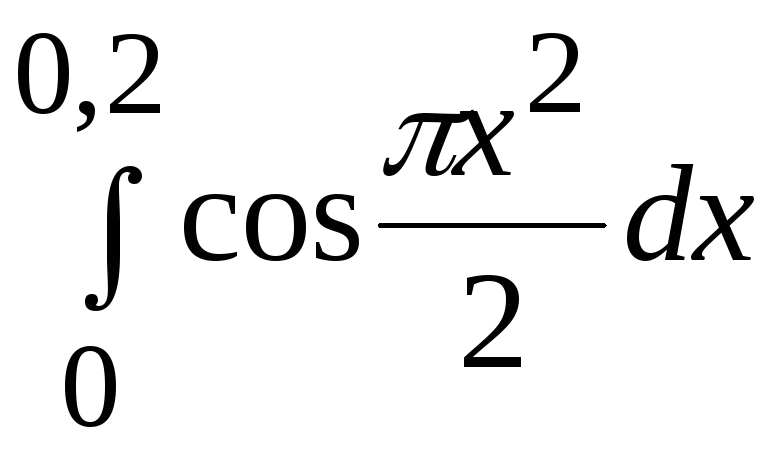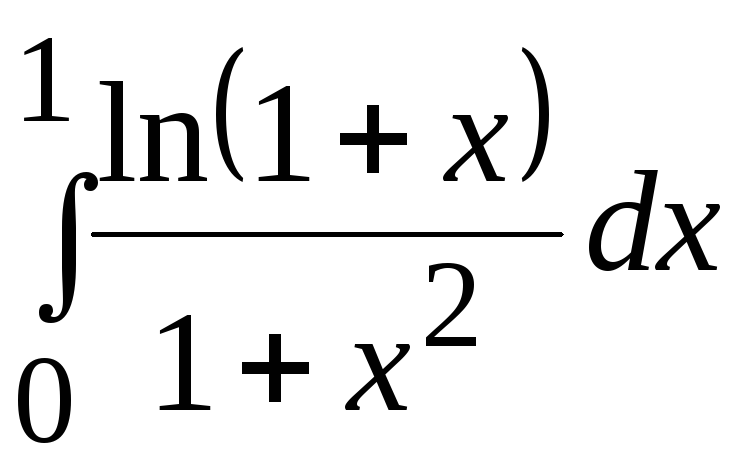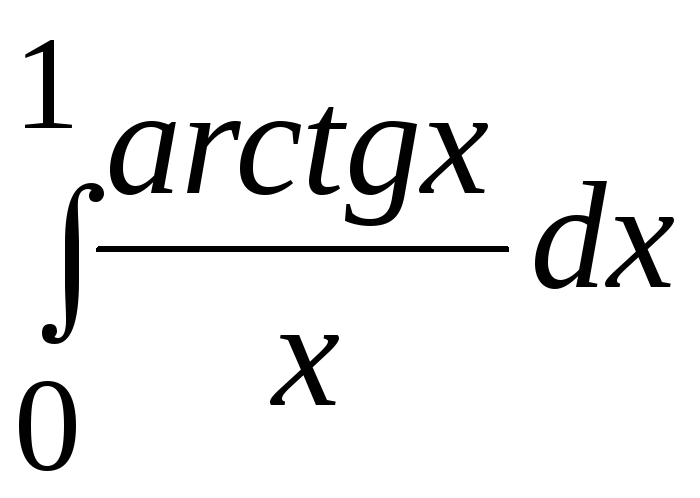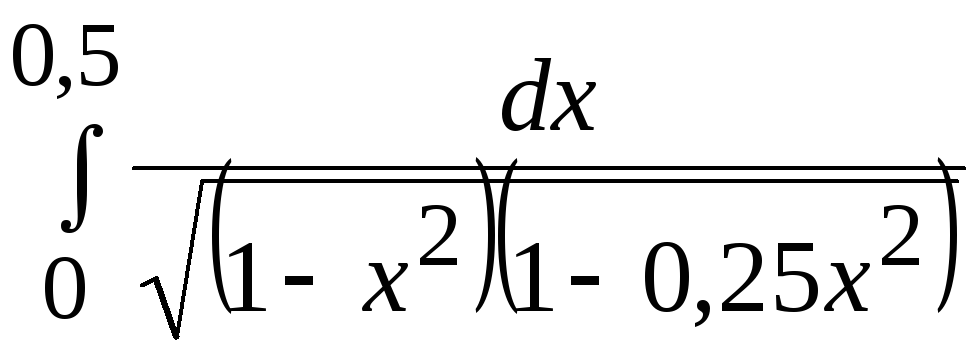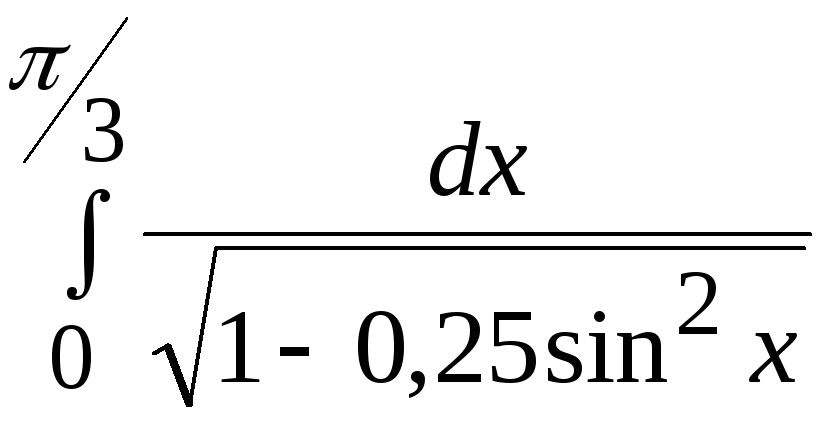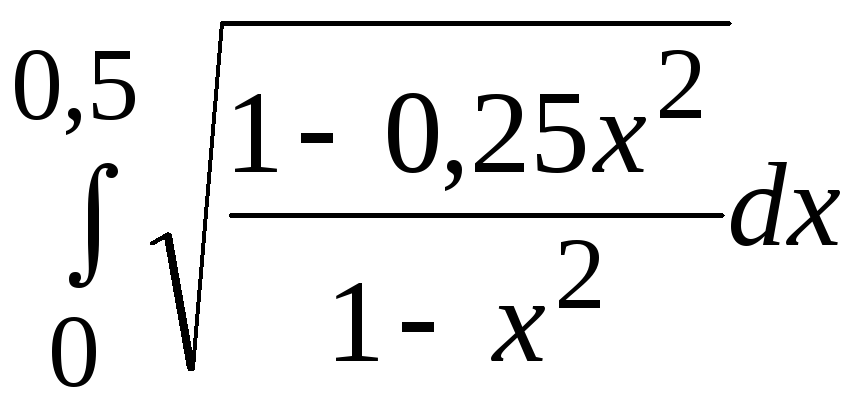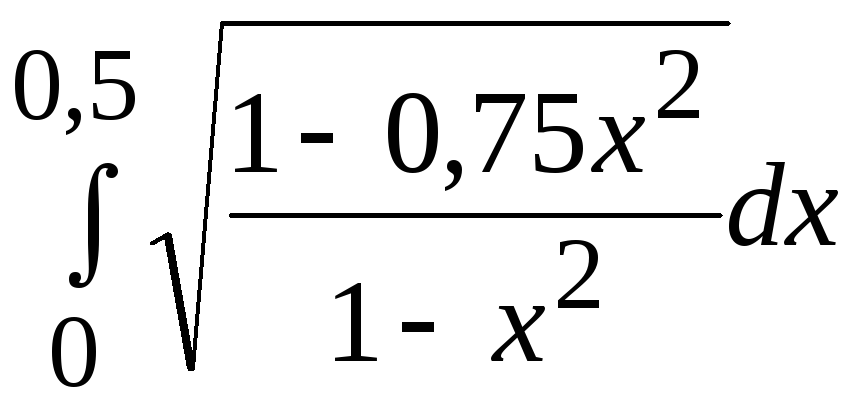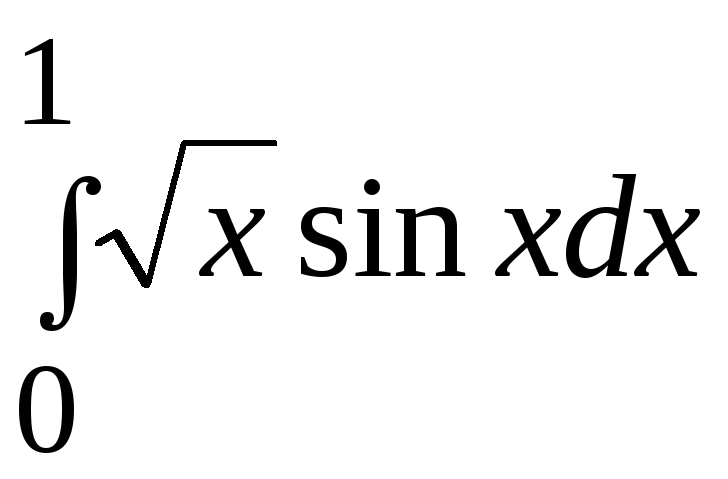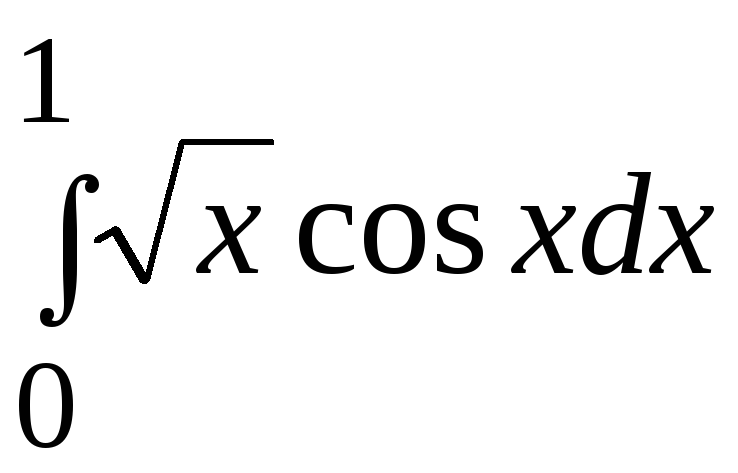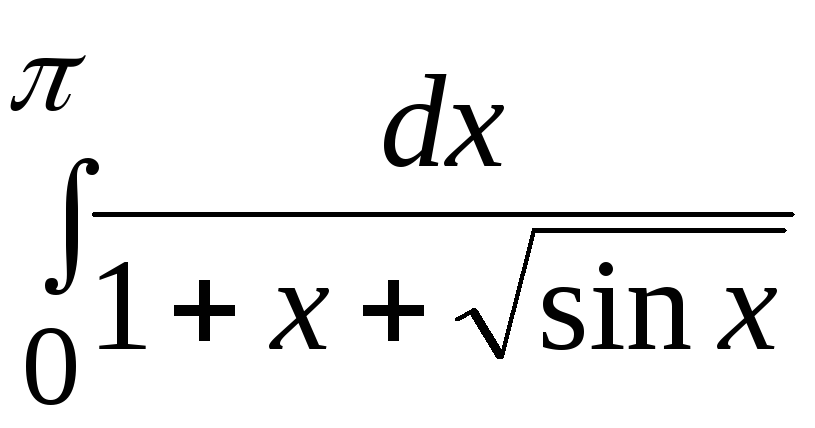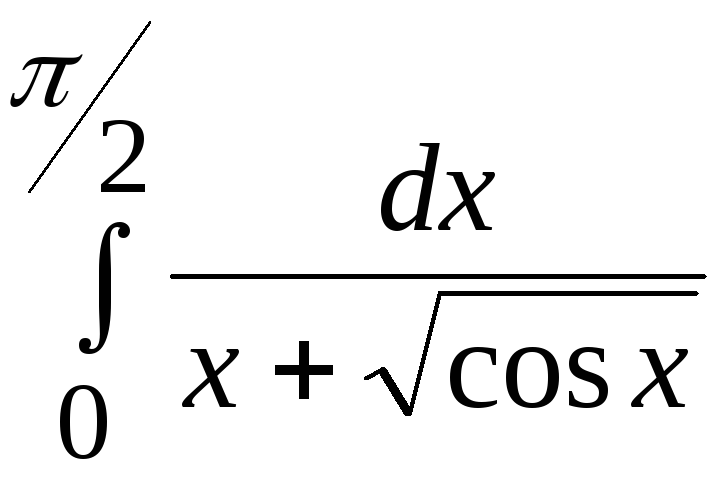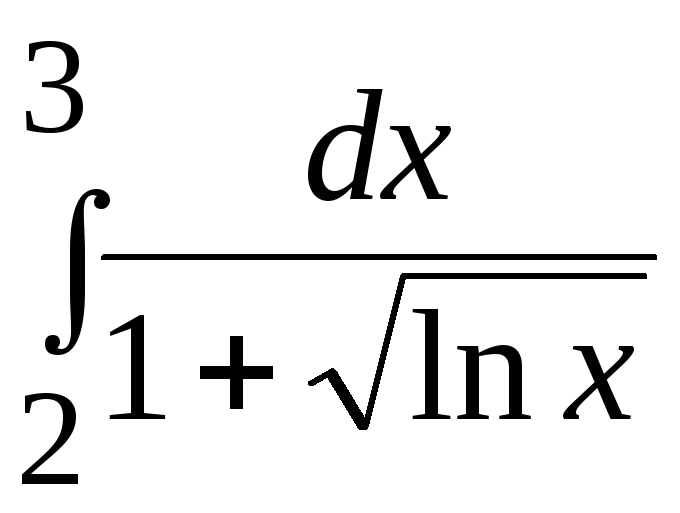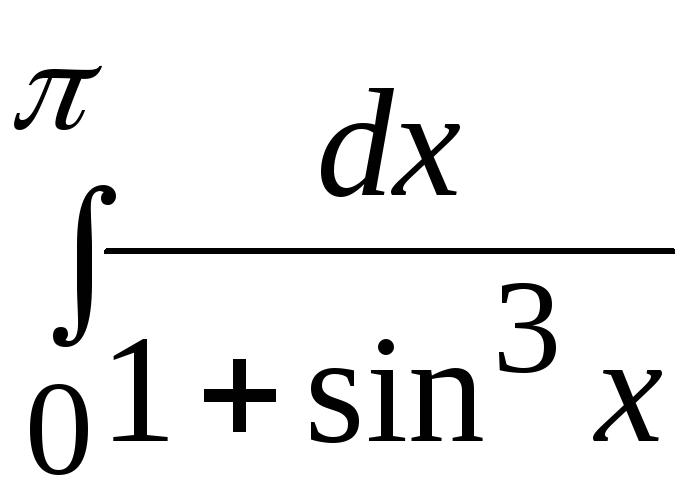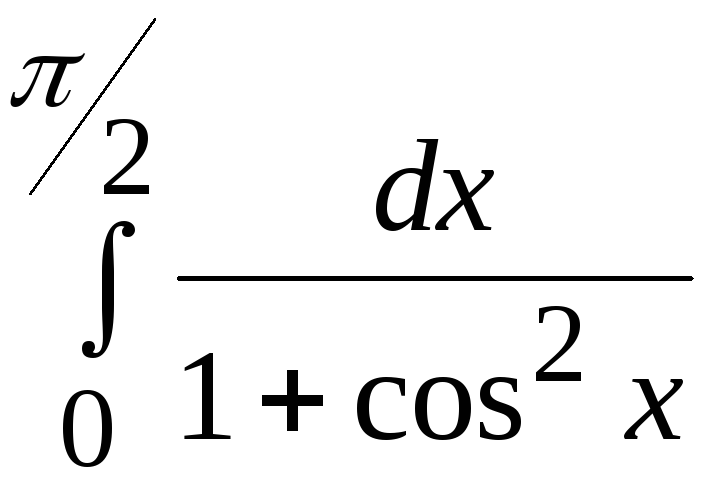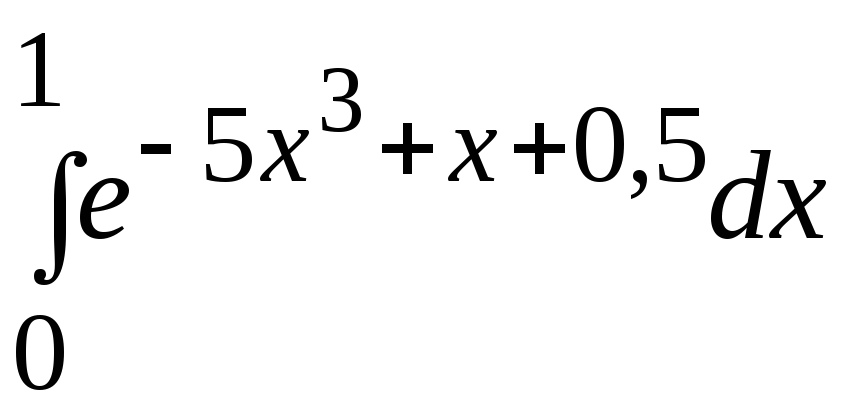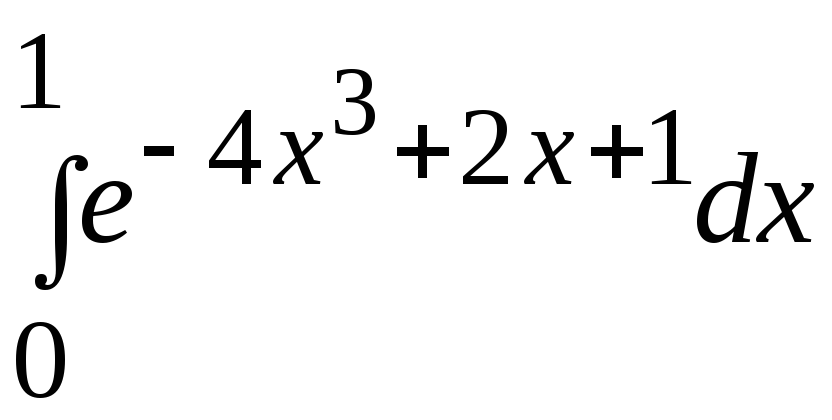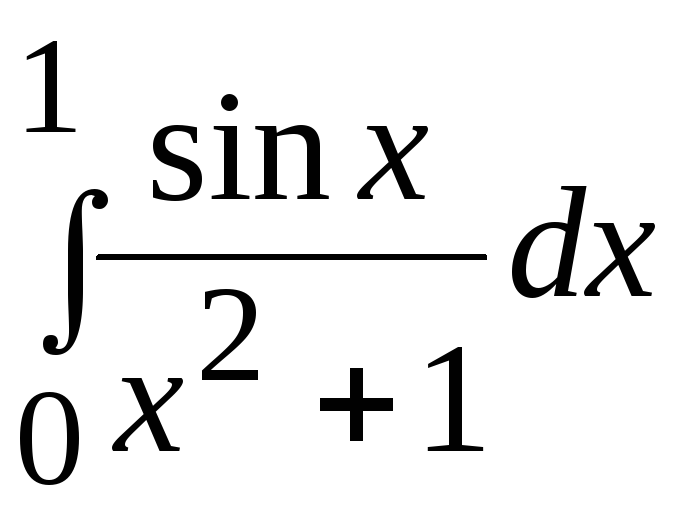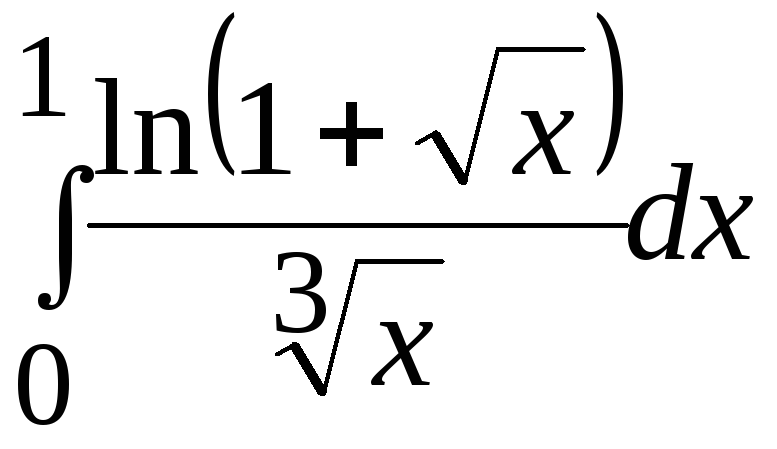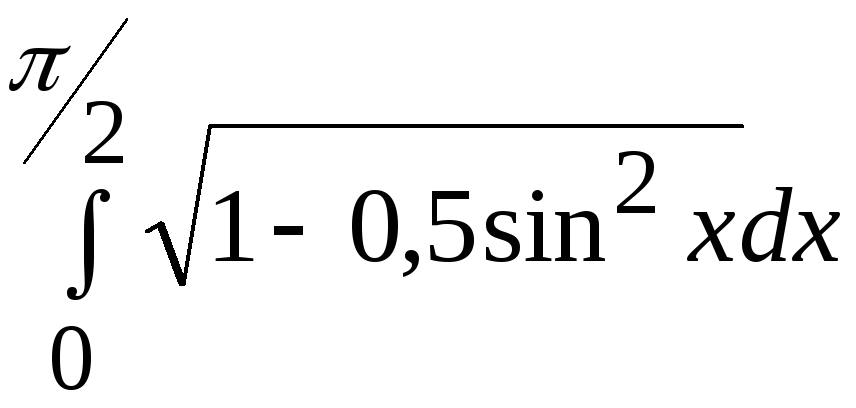Варіанти завдань

1. 

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

20. 

21. 

22. 

23. 

24. 

Лекція 7. Методи рішення звичайних диференціальних рівнянь

У якій розглядаються найпростіші аналітичні послідовних наближень і рядів Тейлора) і чисельні (Эйлера, трапецій і Рунге-Кутта) методи рішення задачі Коші звичайних диференціальних рівнянь.

1. Вступні зауваження

Нижче розглядаються деякі, що одержали поширення аналітичні й чисельні методи рішення задачі Коші для звичайного диференціального рівняння першого порядку

(1)

. (2)

Умова (2) називається початковим.

Достатні умови можливості розв'язання таких задач формулюються теоремою існування й одиничності, один з найбільш простих варіантів якої, полягає в наступному.

Нехай у крапці (x₀, y₀) і деякої її околиці функція f(x, y) і її похідна безперервні. Тоді існує єдина функціяy=y(x) безупинно дифференцируемая в крапці x₀ і деякої її околиці задовольняючому диференціальному рівнянню (1) і початковій умові (2).

Надалі ці умови передбачаються виконаними.

Аналітичними називають методи, що дозволяють одержати вираження, що описують наближені значення шуканої функції в будь-якій крапці заданого відрізка [a, b]. Чисельними називаються методи, що дозволяють одержати наближені значення лише в окремих крапках заданого відрізка.

2. Аналітичні методи

Розглянемо два з них.

Метод послідовних наближень. Представимо в рівнянні (1) у вигляді відносини диференціалів, тоді

Далі, інтегруючи обидві частини отриманого співвідношення на проміжку [x₀, x] одержуємо

,

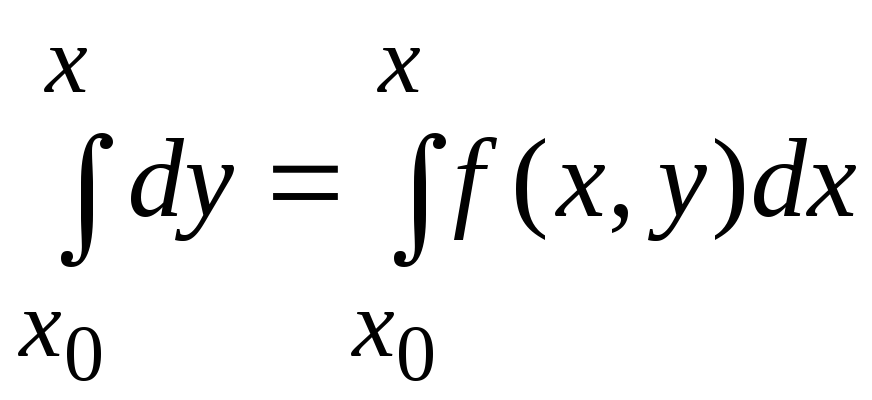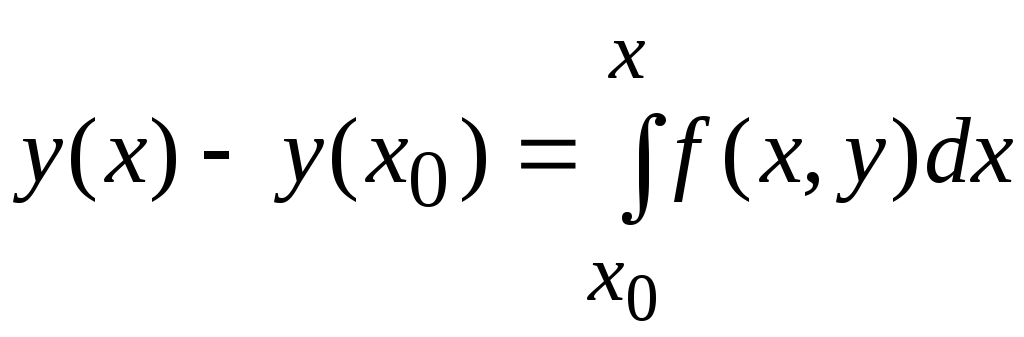
або

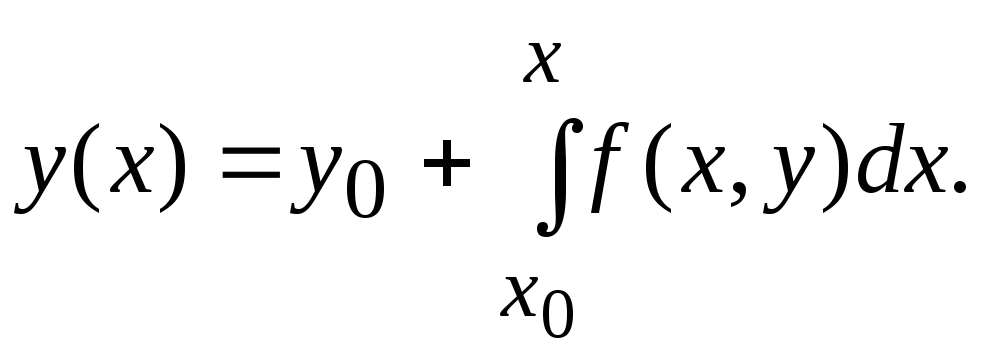(3)

Співвідношення (3) являє собою інтегральне рівняння, еквівалентне задачі (1), (2). На його основі будується наступний обчислювальний процес

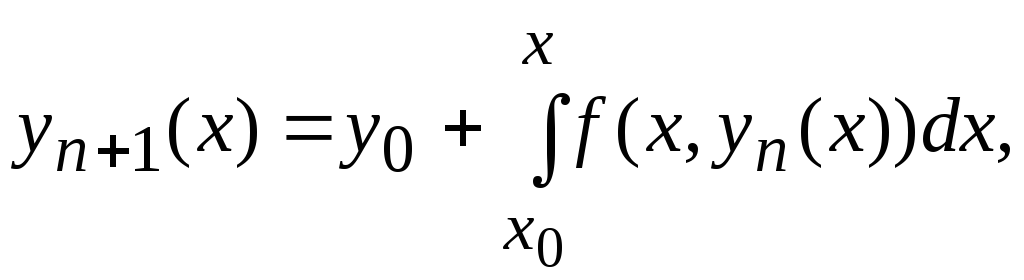(4)

де , що і називаєтьсяметодом послідовних наближень. За певних умов послідовність функції сходиться до точного рішення задачі (1), (2). А саме,

Нехай у прямокутнику виконані умови теореми існування й одиничності й. Тоді в проміжку, депослідовність (4) сходиться до точного рішення. Причому справедливо наступну оцінку

де .

Для ілюстрації цього методу розглянемо наступний

Приклад. Знайти рішення задачі Коші

, .

Знайти два перших наближення до рішення, оцінити погрішність.

Рішення. Візьмемо як область квадрат [-1, 1; -1, 1]. Тут,,. Тоді

т.е. М=2,

т.е. N=2,

.

Погрішність n-го наближення

,

звідси погрішність другого,- .

Знайдемо наближення Думаючи, що, з (4) маємо

,

т.е. .

Тоді

т.е.

Зауваження. У тому випадку, коли дана погрішність наближеного рішення число ітерацій, тобто послідовних наближень, можна знайти, зажадавши

Так, наприклад, у розглянутому прикладі

,

звідки й значеннявстановлюється послідовним перебором.

Метод рядів Тейлора. У цьому випадку рішення задачі (1), (2) шукається у вигляді ряду

.

Значення похідних, необхідних для побудови рішення перебувають шляхом послідовного диференціювання рівняння (1). Так, безпосередньо з нього треба

Далі,

,

тоді

і т.д.

Очевидно, що дана процедура дозволяє одержати рішення з як завгодно високою точністю лише в тому випадку, коли функція є нескінченно дифференцируемой у крапціВ противному випадку даний метод може бути взагалі не застосуємо. Див., наприклад, задачу

де вже не існує.