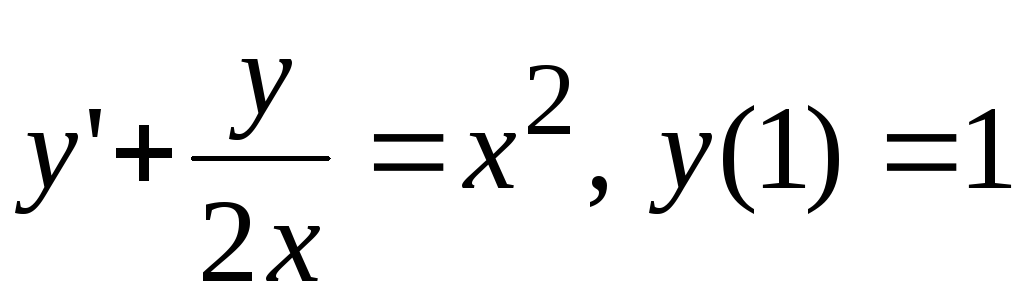Завдання
1. Знайти методом Пикара три перших наближення рішення заданої (відповідно до варіанта завдання) задачі Коші для звичайного диференціального рівняння першого порядку. Привести всі необхідні розрахунки. Побудувати графіки відповідних функцій.
2. Для тої ж задачі Коші за допомогою ручного прорахунку знайти інтегральну криву методом Рунге-Кутта 4-го порядку на відрізку одиничної довжини (починаючи від X0) із кроком 0,2. Привести всі проміжні розрахунки. Остаточні результати розрахунку звести в таблицю. За результатами побудувати графік.
3. Побудувати Simulink-Модель для заданої задачі Коші за умовами попереднього пункту. Зрівняти результат (представлений у вигляді графіка) з результатом п.2.
Варіанти завдань
Лекція 8. Основи спектрального аналізу
У якій нагадуються основні положення теорії рядів Фур'є, виробляється висновок комплексної форми й приводиться їхній дискретний аналог для рівновіддалених вузлів.
Елементи загальної теорії
Нагадаємо основні положення теорії рядів Фур'є.
Нехай
є деяка функція
,
задана на проміжку
й розглядається нескінченна система
функцій
.
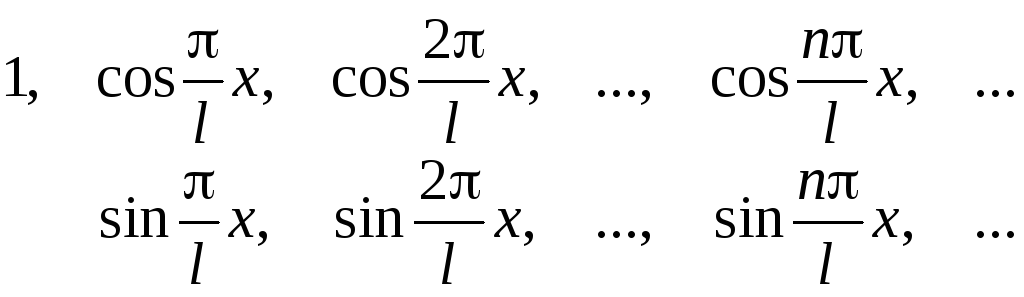Ставиться задача про подання даної функції у вигляді тригонометричного ряду
(1)
Таке подання за певних умов можливо і його коефіцієнти обчислюються по наступних формулах
(2)
Тригонометричний
ряд (1) з коефіцієнтами (2) називається
поруч
Фур'є
функції
.
Справедлива наступна теорема про розкладність (т. Дирихле):
Якщо
кусочно-монотонна функція й має не
більш, ніж кінцеве число крапок розриву
першого роду, то її ряд Фур'є (1), (2)
сходиться до значення
в крапках її безперервності й до
середнього арифметичного її однобічних
меж у крапках розриву.
Так,
наприклад, якщо
крапка розриву
,
то сума ряду Фур'є в цій крапці дорівнює
- (Малюнок
1),
де
,
.
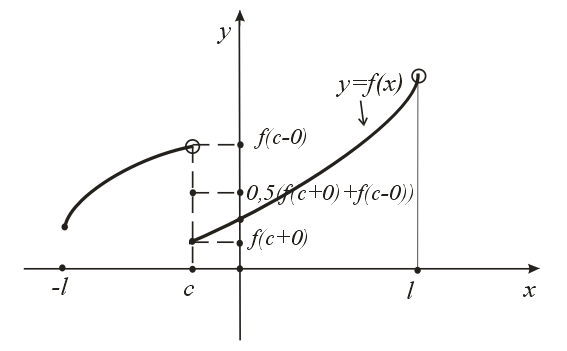
Малюнок 1. Пояснення до теореми Дирихле
Т.о. за
винятком, бути може, кінцевого числа
крапок сума ряду Фур'є (1), (2) дорівнює
.
Зауваження
1. У
крапках
ряд Фур'є сходиться до середньої
арифметичної правої й лівої меж функції
в крапках
відповідно.
Оборотний увага на особливості розкладання в ряд Фур'є парних і непарних функцій.
Якщо
парна на відрізку
,
те
,
також парна, а
,
- непарна. Тому коефіцієнти
і розкладання (1) приймає вид
Якщо ж
функція
непарна, то
також непарна, а
,
- парна.
Тому
,
і розкладання (1) приймає вид
Зауваження
2. Вираження
в розкладанні (1), уводячи допоміжний
кут, можна представити у вигляді
,
де
й ряд у цілому
Тоді
доданки
називаютьсягармонійними
складовими
або гармоніками,
коефіцієнти
-амплітудами
гармонік,
частотами,
-початковими
фазами.
Іноді гармоніка
називаєтьсяосновний,
гармоніки
,
-побічними.
Зауваження
3. Іноді
тригонометричні розкладання заданої
функції будуються на проміжку
.
У цьому випадку розглядається система
тригонометричних функцій
1,
,
і розкладання має вигляд
(3)
де
(4)
.
Теорема
Дирихле для проміжку
формулюється відповідно аналогічним
образом.
Комплексна форма рядів Фур'є
У додатках досить популярної є комплексна форма рядів Фур'є. Їхнє одержання базується на формулах Эйлера
звідки
,
. (5)
Приведемо комплексну форму для розкладання (3). З (4) з використанням (5) маємо
або
,
де
.
Аналогічним образом,
,
або
Тоді гармонійна складова ряду (3)
і
ряд, у цілому,
(6)
де
,
,
,
.
(7)
Розкладання (6), (7) і є шуканим.
Оборотний увага, що амплітуда n-ой гармоніки в цьому випадку дорівнює
.