4.3. Метод послідовних наближень
У цьому випадку рівняння (4.1) приводиться до виду
(4.5)
Далі,
вибирається початкове наближення
до рішення й на основі (4.5) за правилом
(4.6)
будується
послідовність
.
Розглянемо
відображення, формоване функцією
.
Нехай
,
- деякі довільні значення змінної
,
оцінимо величину
.
Маємо
де
.
Звідси випливає наступне твердження.
|
Якщо
|
або те ж
для
,
то відображення
є стискаючим. Отже, ітераційний процес
у цьому випадку сходиться.
Погрішність n-го наближення визначається співвідношенням (3.10).
Зупинимося на закінчення на процедурі приведення рівняння (4.1) до виду (4.5). Один з її варіантів полягає в наступному:
- вихідне
рівняння;
- де m,
- підлягаючому визначенню параметр;
- нова
форма рівняння;
,
де
- необхідна форма.
Нарешті, значення параметра m вибирається з умови
для
.
4.4. Завдання
Шляхом ручного прорахунку знайти корінь заданого рівняння двома методами (із чотирьох розглянутих) із заданою точністю. Відділення корінь провести графічно . Привести всі необхідні проміжні обчислення. Результати звести в підсумкову таблицю:
|
№ ітерації |
Xn |
|Xn-Xn-1| або |Bn-An| |
F(Xn) |
|
|
|
|
|
|
|
|
|
|
Зауваження. Для кожного рівняння необхідно знайти один корінь. Якщо рівняння має більше одного кореня, необхідно відшукати найближчий до початку координат.
Номер рівняння вибрати по формулі: k+21*( q-1).
Тут k - номер студента в списку групи; q=1 для групи А и 2 для групи Б.
Припустима погрішність обчислюється по формулі:
Номера застосовуваних методів ( 1-дихотомії; 2-хорд; 3-дотичних; 4-прості ітерації) обчислити по формулі:
N1=( k-q)MOD 2+1; (перший метод)
N2=[(k+q)DIV 2]MOD 2+3 (другий метод).
Варіанти до завдання
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
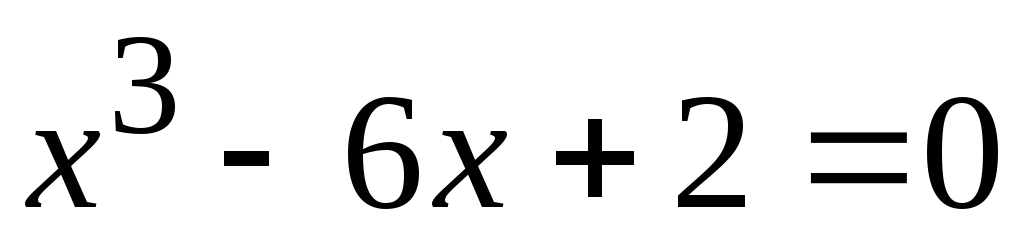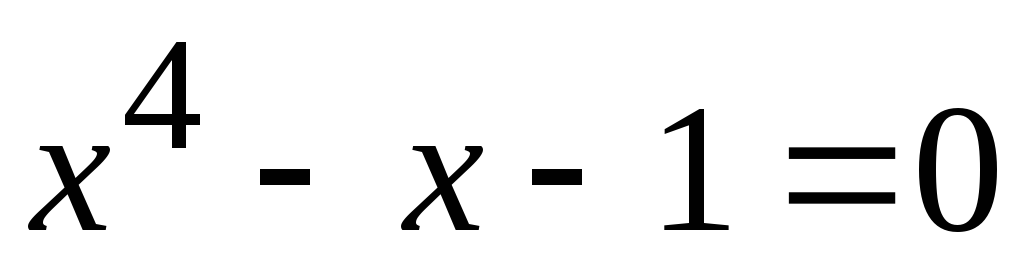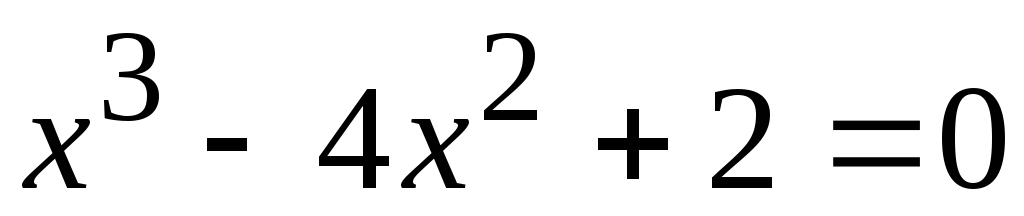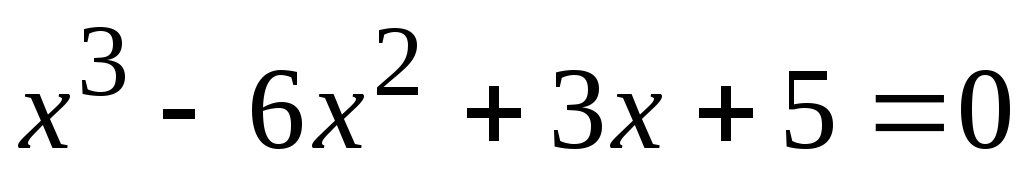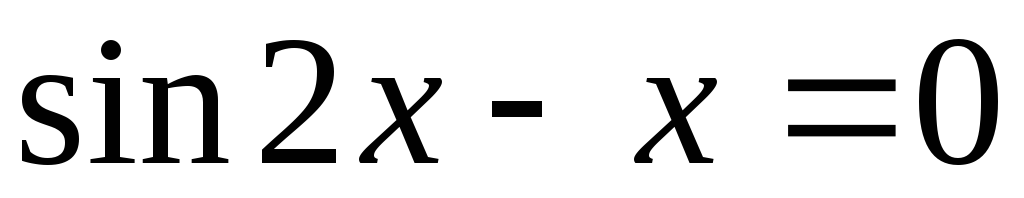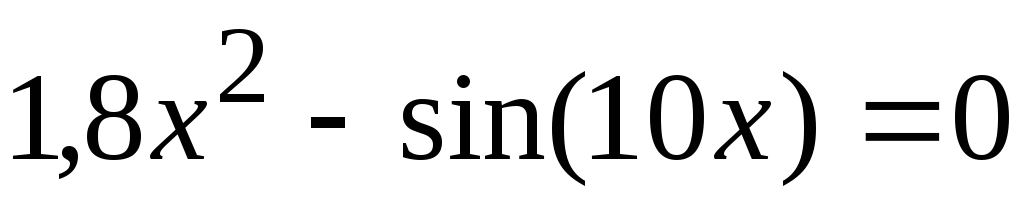
Лекція 5. Рішення систем нелінійних рівнянь
У якій, розглянуті вище, методи Ньютона й ітерацій узагальнюються на випадок систем нелінійних рівнянь.
Нижче обмежимося розглядом методу ітерацій і методу Ньютона, які належать до числа основних.
Метод ітерацій
Передбачається, що система рівнянь представлена у вигляді
, (5.1)
де
,
- функції, що диференціюються ,змінних
в областіD,
що містить рішення системи (5.1). Позначивши
через
і
,
систему (5.1) можна представити в більше
зручному для викладу виді
.
Нехай
,
- деяке наближення до шуканого рішення.
Тоді обчислювальний процес, организовуваний
по формулі
, (5.2)
де k = 0, 1, 2, … називається методом ітерацій. Якщо при обчисленні чергової координати k+1 – го наближення використовувати обчислені перед цим значення попередніх координат цього ж наближення, одержимо модифікацію, називану методом Зейделя. У ній алгоритм обчислень описується в такий спосіб
.
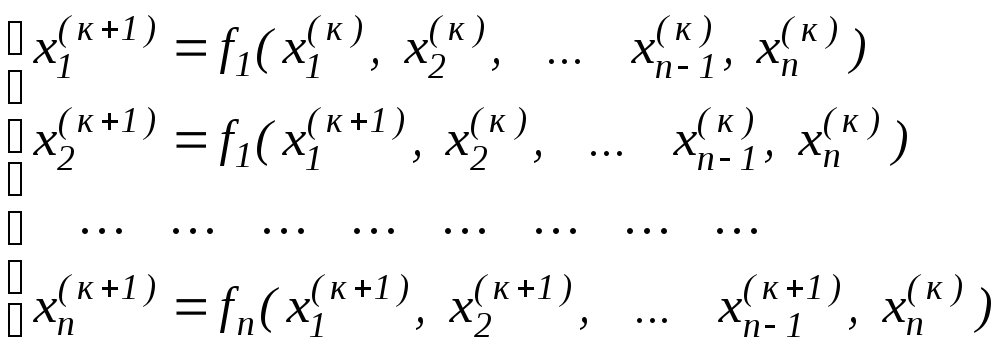За певних умов метод ітерацій (5.2) сходиться до точного рішення системи (5.1). Установимо ці умови, використовуючи, як і вище, поняття стискаючого відображення.
В
n-мірному
просторі
набір функцій
визначає деяке відображення,,
що нескiнченно диференціюється. Вище
(див. Лекція 3) було показано, що збіжність
ітераційної послідовності забезпечується
збіжністю утворюючого її відображення.
Нехай
- довільні точки
,
оцінимо
.
Припустимо, що величина
досить мала й у тейлоровських розкладаннях
функцій
у точцi
дозволено обмежитися величинами першого
порядку малості. Тоді
,
де
,
(5.3)
- матриця
Якобi
системи функцій
.
Якщо
в областіD,
відображення
є
стискаючим і є підстави вважати, що
ітераційний процес (5.2) сходиться до
рішення системи (5.1). Більш виразно це
формулюється у вигляді наступноїтеореми:
Нехай
в області D
система (5.1) має, принаймні, одне рішення,
що належить її внутрішньої частини й
норма матриці Якобi
в замиканні
областіD
менше
одиниці. Тобто,
таке
,
що
.
Тоді в областіD
система (5.1) має рішення й ітераційний
процес (5.2) сходиться до одному з
рішень при будь-якому
виборі
початкового наближення
.
Погрішність k-го наближення, як і раніше (див. Лекція 3), можна оцінити співвідношенням
.
Зауваження. Нерідко вихідна система рівнянь буває представленої в неявній формі
, (5.4)
де якобiан системи
.
Тоді для приведення (5.4) до виду (5.1), що забезпечує збіжність, можна використовувати припущування, аналогічні висловленим вище (див. Лекція 4). А саме, помножимо обидві частини (5.4) на деяку неособливу квадратну матрицю А
,
додамо, далі до обох частин х
,
позначимо
і зажадаємо, щоб
.
Із цього співвідношення можна визначити коефіцієнти матриці А. Якщо це зробити важко для всієї області D, то зазначену операцію можна робити покроково на кожному кроці ітераційного процесу.
Пояснимо це на прикладі двох рівнянь
.
Позначимо
.
Тоді система (5.1) приймає вигляд
.
Звідси
.
Задамо
далі,
і зажадаємо, щоб
.
Звідси, за правилом Крамера, наприклад,
,
.
Аналогічним чином, зажадавши
Знайдемо с и d.
Проводячи
зазначені перетворення на кожному кроці
ітераційного процесу, тим самим створюємо
умови для збіжності його зі швидкістю
в цілому.