3.5.3 Основные (типовые) законы распределения нсв

НСВ имеетравномерное распределение на участке , если ее плотность на этом участке постоянна:

График имеет вид:

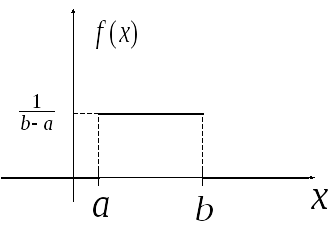
Функция распределения

Равномерное распределение зависит от двух параметров и.

Числовые характеристики:

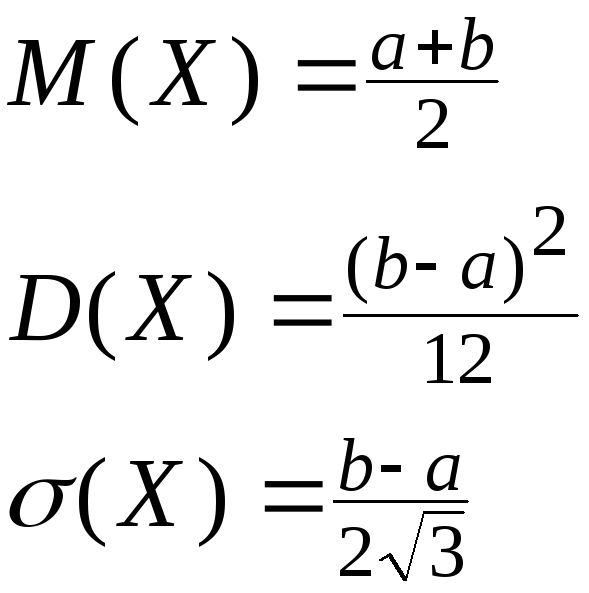(3.25)

Частный случай равномерного закона распределения НСВ – НСВ равномерно распределенная на интервале (0,1), для которой

, ,

Значения НСВ называютсяслучайными числами.

Вероятность попадания НСВ в результате испытания в интервалравна его длине:

НСВ имеетпоказательное (экспотенциальное) распределение, если её плотность выражается формулой:

где - постоянная положительная величина.

График имеет вид

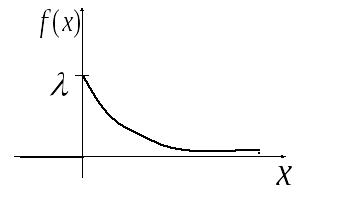
Функция распределения

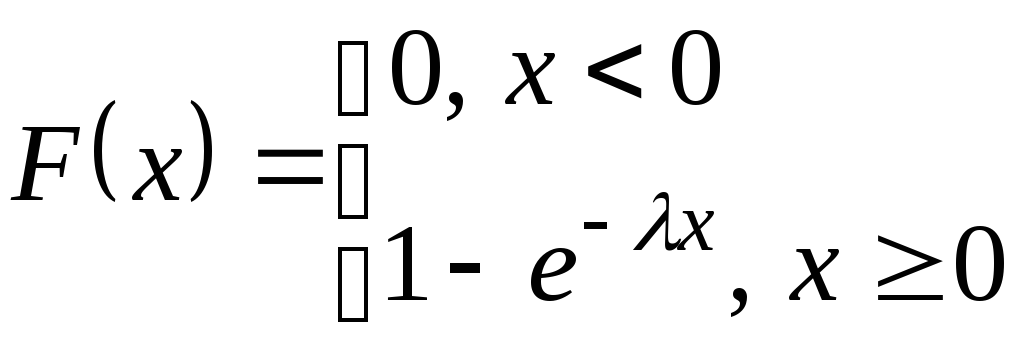
График функции

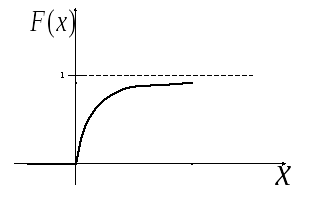
Показательное распределение зависит от одного параметра .

Числовые характеристики:

(3.26)

т.е.

Вероятность попадания НСВ , распределенной по показательному закону, в интервалвычисляется по формуле:

(3.27)

Пример:

1. По соединительной линии между пунктами иосуществляются телефонные разговоры со средней длительностью 4 мин. для направленияи 3 мин. для. Вызовысоставляют 55% всех вызовов. Найти вероятность того, что некоторый разговор длится дольше 6 минут.

Решение.

Длительность разговора в телефонных сетях (время занятости линии связи) имеет показательное распределение. Если - средняя длительность разговора, то- интенсивность освобождения линии связи.

И вероятность того, что разговор случайной длительностью закончится до момента:

(3.28)

а вероятность того, что разговор не закончится до момента :

(3.29)

Тогда

По формуле полной вероятности (2.20)

. Элемент отказывает в среднем 1 раз за 50 часов непрерывной работы. Считая, что время безотказной работы распределено по показательному закону, найти вероятность отказа за 100 часов.

Решение.

Пусть элемент начинает работать в момент , а через времяпроисходит отказ. Обозначим черезНСВ - время безотказной работы элемента.

Тогда интегральная функция

(3.30)

определяет вероятность отказа за время , а функция надежности

(3.31)

где - интенсивность отказов ;

определяет время безотказной работы за время .

Из анализа формулы следует, что вероятность безотказной работы элемента на интервалене зависит от времени работы до начала рассматриваемого интервала, а зависит только от длительности времени.

НСВ имеет общеенормальное распределение с произвольными значениями и, если её плотность

(3.32)

или нормированное распределение с параметрами и, если её плотность

(3.33)

есть функция Гаусса и имеет свойства:

- четности ;

- если , то;

- табулирована на отрезке .

График плотности нормального распределения называют нормальной кривой (кривой Гаусса)

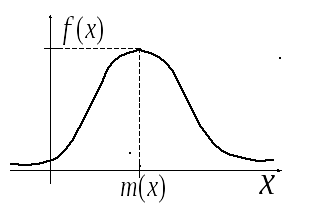
Нормальная кривая.

1. Определена на всей оси

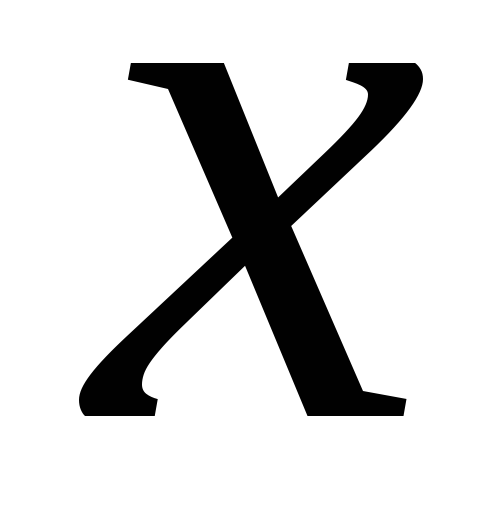
2. Принимает только положительные значения.

3. Ось 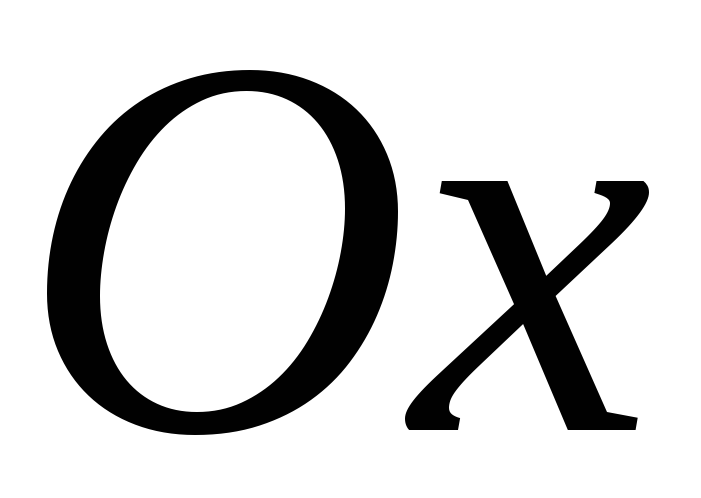является горизонтальной асимптотой графика.

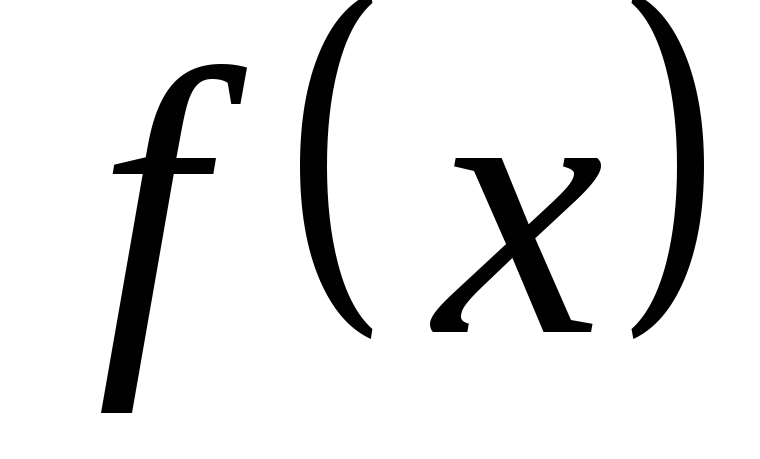4. Имеет только один максимум в точке .

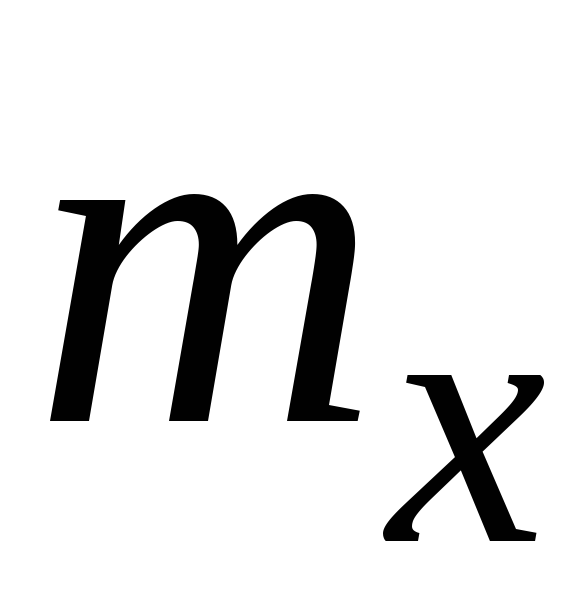5. Симметрична относительно прямой .

6. Точки на кривой с координатами

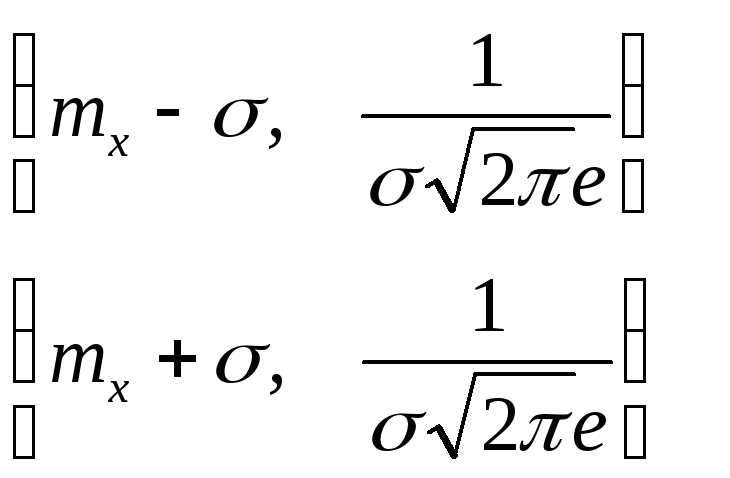
являются точками перегиба.

При изменении форма нормальной кривой не изменяется, она сдвигается вдоль осивправо, есливозрастает и влево, еслиуменьшается.

Изменение изменяет форму нормальной кривой. При возрастаниикривая становится более пологой, т.е. прижимается к оси. При уменьшениикривая становится более острой.

Интегральная функция общего нормального распределения

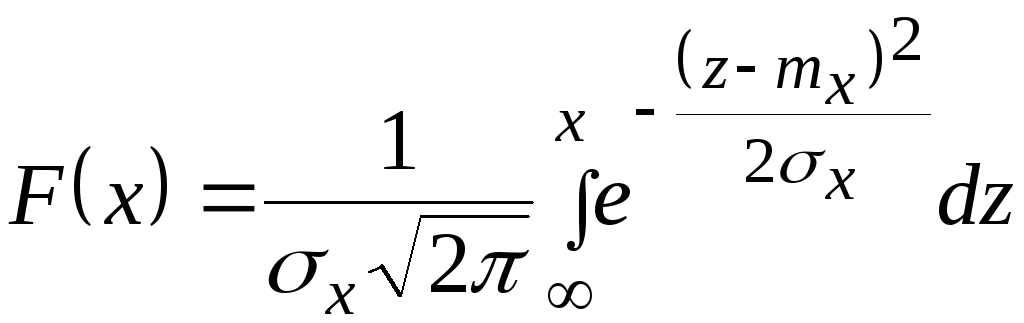(3.34)

а нормированного распределения

(3.35)

есть функция Лапласа

(3.36)

Функция Лапласа обладает свойствами:

- нечетности ;

- если , то;

- монотонно возрастает (если , то);

- табулирована на отрезке .

Нормальное распределение зависит от двух параметров и.

Вероятность попадания НСВ в интервал

(3.37)

Если участок симметричен относительно точки, то вероятность попадания в него

,

где - половина длины участка.

Пример:

1. Проверить правило 3-х сигм

Решение.

т.е. возможные значения нормальной НСВ попадут в интервалс вероятностью.

2. На автоматическом токарном станке изготовляют болты, номинальная длина которых 40мм. В процессе работы станка наблюдаются случайные отклонения, распределенные по нормальному закону с и. При контроле бракуются все болты, размеры которых отличаются от номинального больше, чем на 2мм. Найтиотклонение, если известно, что брак составляет 10% всей продукции.

Решение.

- отклонение размера случайно взятого болта от номинального

Нормальный закон является наиболее важным, как в теории, так и на практике, т.к. большинство наблюдаемых явлений подчиняются этому закону и он считается предельным законом, к которому приближаются другие законы распределения при определенных часто встречающихся типичных условиях.