5.2 Теория оценок

Теория оценок определяет методы и способы статистической оценки неизвестных параметров теоретического распределения случайной величины по совокупности экспериментальных данных. При этом часто допускается, что закон распределения генеральной совокупности известен, но неизвестны параметры этого закона (математическое ожидание, дисперсия), которые необходимо оценить (приближённо найти) по выборочной совокупности.

Статистической оценкой неизвестного параметра теоретического распределения называется функция от выборочных значений (вариант), которая даёт приближённое значение оцениваемого параметра.

Все оценки делятся на точечные и интервальные.

5.2.1. Точечные оценки.

Точечной называется оценка, которая определяется одним числом.

К точечным оценкам предъявляются следующие требования:

- несмещённости;

- эффективности;

- состоятельности.

Пусть –статистическая оценка неизвестного параметра теоретического распределения. Допустим, что по выборке объёмаn найдена оценка . Извлечём из генеральной совокупности другую выборку объёмаn и вычислим. . Повторяя опыт многократно, получим числа,,…,, которые, вообще говоря, различны между собой. Таким образом, оценкуможно рассматривать как случайную величину, а числа,,…,– как её вложенные значения.

Несмещённой называют статистическую оценку , математическое ожидание которой равно оцениваемому параметрупри любом объёме выборки, т. е.

.

Смещённой называют оценку, математическое ожидание которой не равно оцениваемому параметру, т. е.

.

Эффективной называют статистическую оценку, которая при заданном объёме выборки n имет наименьшую возможную дисперсию.

Состоятельной называют статистическую оценку, которая при стремится по вероятности к оцениваемому параметру, т. е.

,

где – бесконечно малая величина.

Оценка генеральной средней выборочной средней выполняется по формуле (5.4) и является немещённой и состоятельной, если выборка повторная и несмещённой, если выборка бесповторная.

В качестве оценки генеральной дисперсии принимают исправленную выборочную дисперсию S².

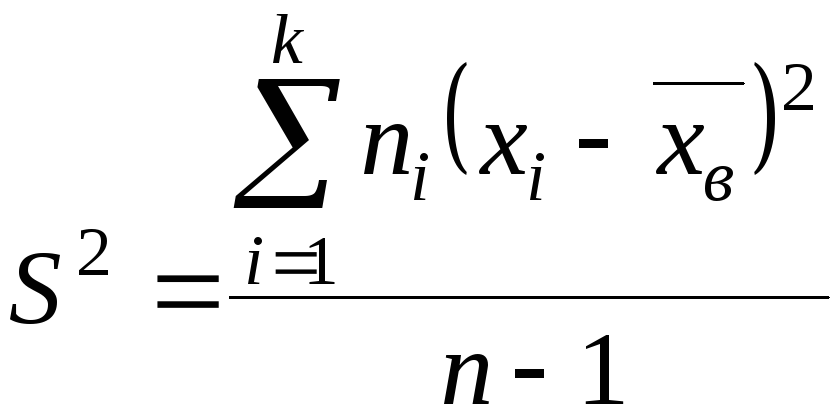(5.24)

или

,

которая удовлетворяет требованию несмещённости. Очевидно, при достаточно больших значениях n D_в и S² различаются мало. На практике S² вычисляется, если n < 30.

Для оценки среднего квадратического отклонения генеральной совокупности используется исправленное выборочное среднее квадратическое отклонение S или выборочное среднее квадратическое отклонение .

. (5.25)

Все рассмотренные оценки (формулы (5.4), (5.11), (5.24), (5.25)) являются точечными.

Точечные оценки используются прежде всего тогда, когда с их помощью выполняются другие расчёты. При этом точечные оценки не несут информации о точности конкретной оценки. При малых объёмах выборки точечные оценки могут значительно отличаться от оцениваемого параметра.

5.2.2 Интервальные оценки

Интервальной называется оценка, которая определяется двумя числами – началом и концомм интервала, в котором находится оцениваемый параметр теоретического распределения с некоторой вероятностью.

Пусть найденная по данным выборки статистическая оценка является оценкой неизвестного параметра. Статистическая оценкатем точнее определяет параметр, чем меньше абсолютная величина разности, т. е., еслии

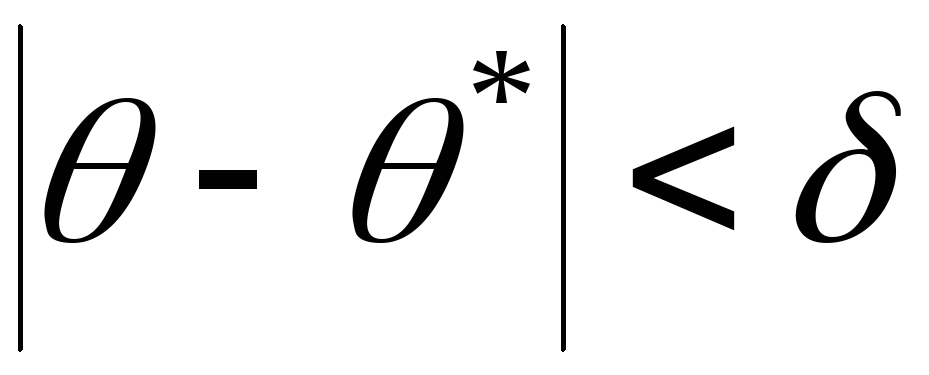, (5.26)

то чем меньше , тем оценка точнее. Таким образом, величинахарактеризует точность оценки.

Т. к. – случайная величина, то нельзя категорически утверждать, чтоудовлетворяет неравенству (5.26). Вероятность, с которой выполняется неравенство (5.26) называетсянадёжностью (доверительной вероятностью).

. (5.27)

Обычно задаётся наперёд в виде числа, близкого к единице, наиболее често – 0,95; 0,99; 0,999.

Заменим неравенство в формуле (5.27) равносильным двойным неравенством:

.

Интервал называютдоверительным, его границы – доверительными границами.

Доверительный интервал покрывает неизвестный параметр с надёжностью.

Если случайная величина X распределено нормально с математическим ожиданием равным a и среднеквадратическим отклонением известным и равным , то по выборке объёмаn можно найти доверительные границы для математического ожидания a по уровнениям

;

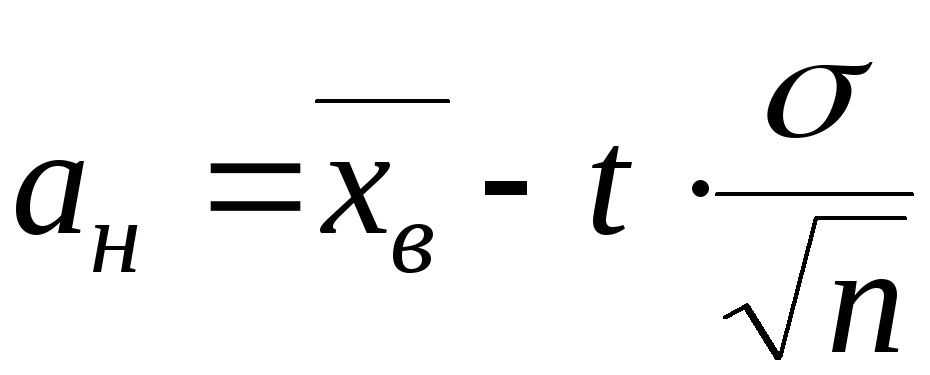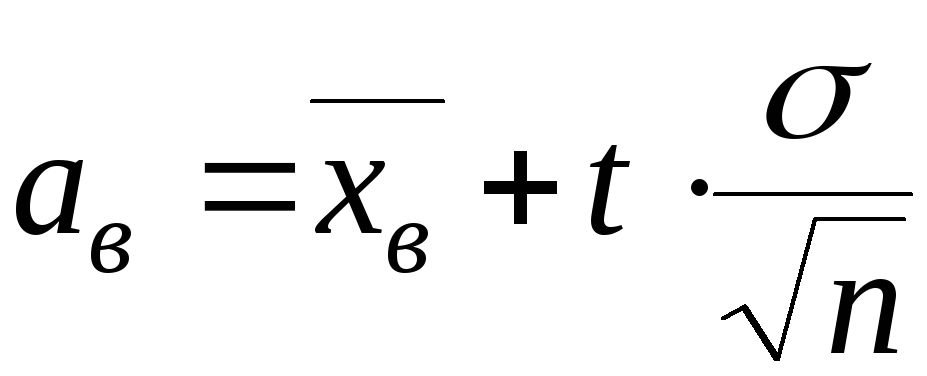, (5.28)

где a_н и a_в – нижняя и верхняя доверительные границы математического ожидания a;

t – коэффициент, определяемый по таблице функции Лапласа, которому соответствует значение функции Лапласа . В этом случае

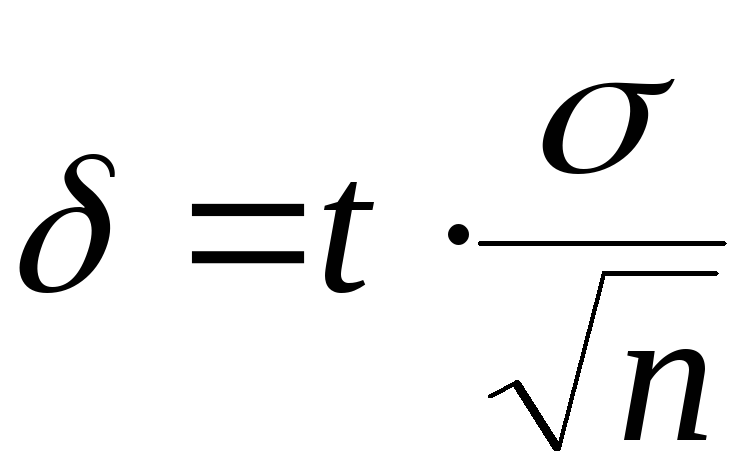. (5.29)

Анализ формулы (5.29) показывает, что

- при возрастании объёма выборки n число убывает и, следовательно, точность оценки возрастает;

- при увеличении надёжности возрастают значенияt (функция является возрастающей) и , что приводит к уменьшению точности оценки;

- если требуется оценить математическое ожидание с наперёд заданной точностью и надёжностью , то минимальный объём выбоки, который обеспечит эту точность находят по формуле

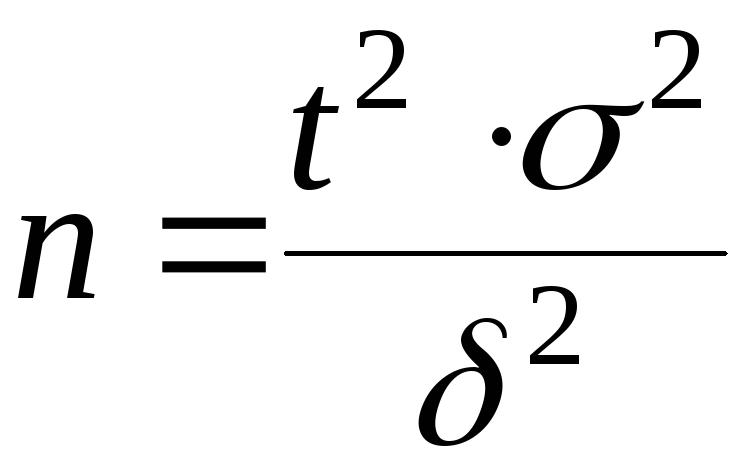. (5.30)

Формула (5.30) используется для повторной выборки, для бесповторной выборки минимальный объём пересчитывают по формуле

, (5.31)

где N – генеральной совокупности.

Пример 1. Случайная величина X имеет нормальное распределение с известным среднеквадратическим отклонением . Найти доверительный интервал для оценки неизвестного математического ожиданияa по , еслии.

Решение.

При условии

;

;

.

Вычисляем

.

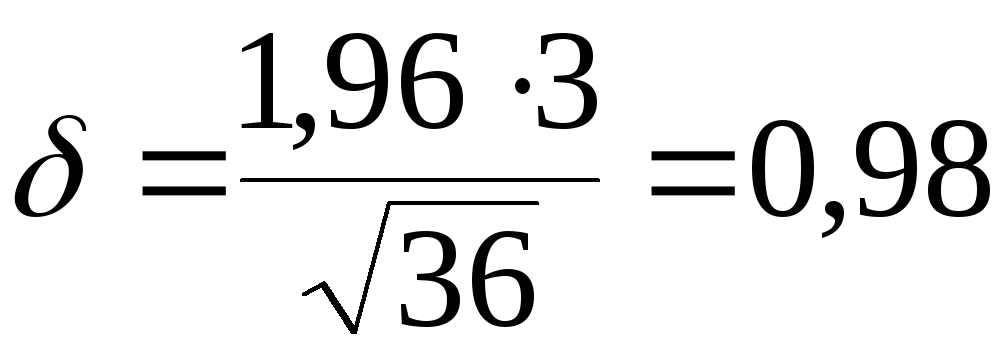Получили искомый доверительный интервал:

;

.

.

Пример 2. Найти минимальный объём повторной и бесповторной выборок для генеральной совокупности с объёмом N=1000 с , при котором точность оценки математического ожидания нормально распределённого признака будет равна0,2 при .

Решение.

;

;

;

.

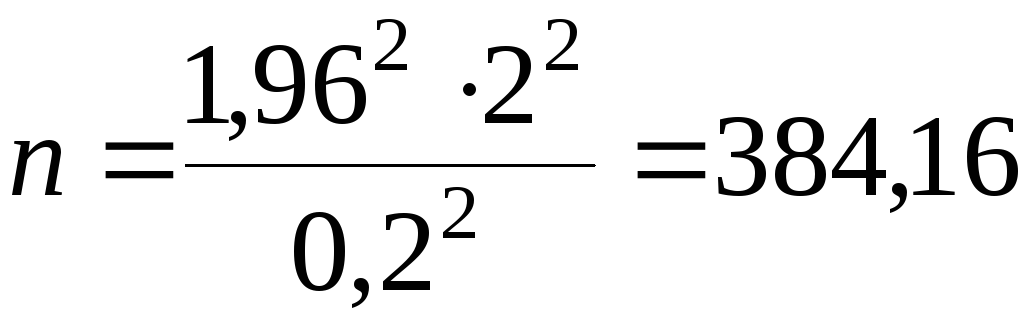Принимаем объём повторной выборки n=385.

Для бесповторной выборки

.

Принимаем объём бесповторной выборки .

Если случайная величина X распределена нормально с математическим ожидание равным a и среднеквадратическим отклонением неизвестным, то по выборке объёма n можно найти доверительные границы для математического ожидания a по формулам

;

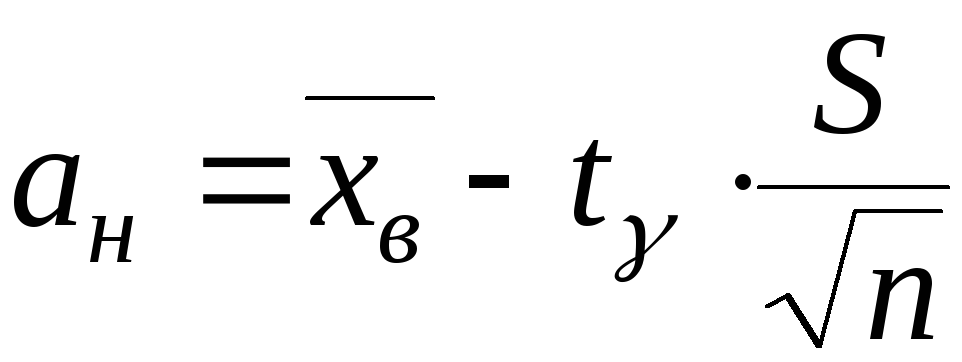, (5.32)

где S – исправленное среднеквадратическое отклонение;

–коэффициент Стьюдента, который определяется по таблице в зависимости от надёжности и числа степеней свободы, равное.

При неограниченном возрастании объёма выборки n распределение Стъюдента стремится к нормальному, поэтому при n>30 в формулах (5.32) можно заменить на .

Если случайная величина X распределена нормально и среднеквадратическое отклонение неизвестно, то оценить его помжно по исправленному среднеквадратическому отклонениюS, рассчитанному для выборки объёма n, по формулам

;

, (5.33)

где ,– нижняя и верхняя доверительные границы среднеквадратического отклонения;

q – коэффициент распределения , определяемый по таблице в зависимости от и объёма выборкиn.

Если q<1, то учитывая, что ,.

Пример. Случайная величина X имеет нормальное распределение. По выборке объёма n=10 найдено исправленное среднеквадратическое отклонение S=0,16. Найти доверительный интервал, покрывающий неизвестное среднеквадратическое отклонение с надёжностью.

Решение.

По таблице найдём q=1,8 (q>0) при и n=10.

Искомые доверительные границы доверительного интервала:

;

.

Практическое применение формулы (5.28) и (5.32) получили для оценки истинного значения измеряемой величины, формулы (5.33) – для оценци точности измерений (точности прибора).

Если случайная величина X имеет биноминальное распределение, то оценить неизвестную вероятность p появления события A в каждом испытании можно, рассчитав доверительные границы по формулам

;

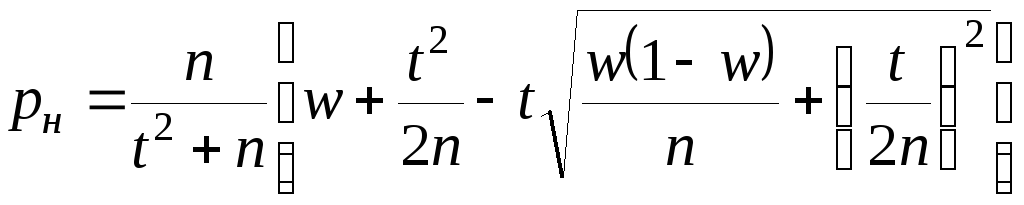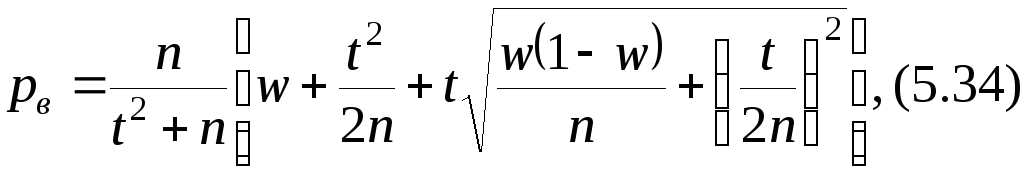
где р_н и р_в – нижняя и верхняя доверительные границы неизвестного значения вероятности p;

w – относительная частота (точечная оценка для p).

,

где m – число появления события A;

n – число испытаний.

Пример. Производят независимые испытания с одинаковой, но неизвестной вероятностью p появления события A в каждом испытании. Найти доверительный интервал для оценки p с надёжностью 0,95, если в 80 испытаниях событие A появилось 16 раз.

Решение.

По условию m=16, n=80, .

Найдём .

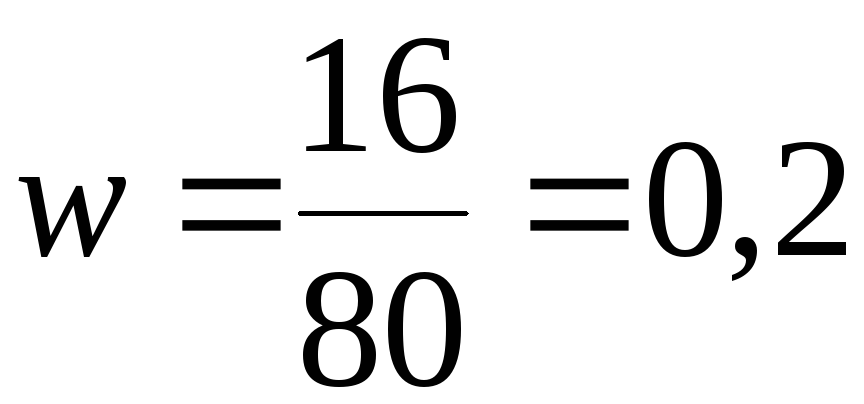Найдём t по таблице функции Лапласа из соотношения .

Подставив n, w, t в формулу (5.34), получим

, .

При больших значениях n (порядка сотен) слагаемые и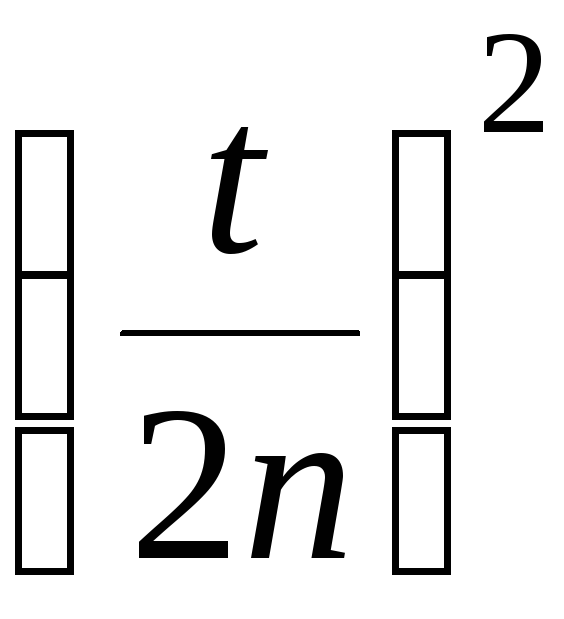очень малы и множитель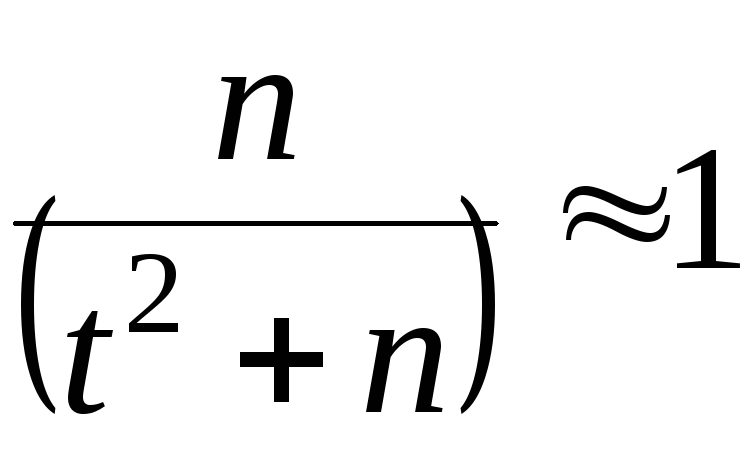, поэтому доверительные границы можно рассчитать по формулам

;

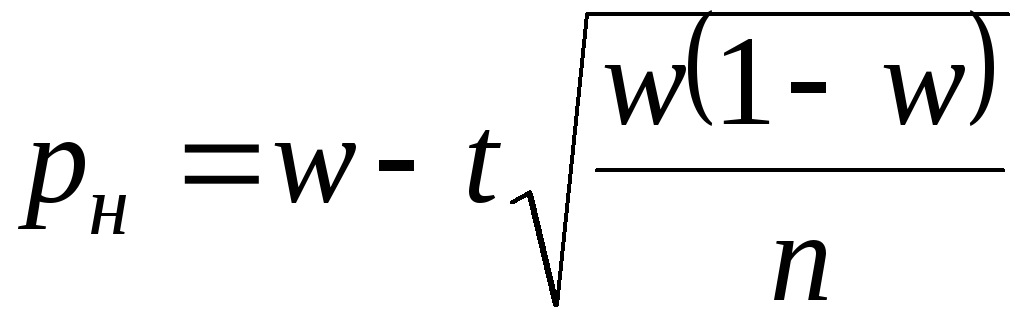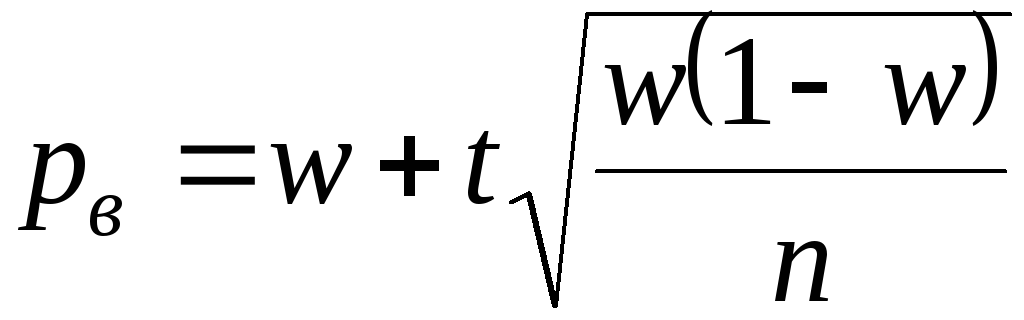. (5.35)