5.3.3 Проверка статистической гипотезы о параметрах распределения

Пусть генеральные совокупности СВ X и СВ Y распределены нормально. По независимым выборкам с объёмами, соответственно равными, n₁ и n₂, извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии и . Требуется по и при заданном значении проверить, H₀ состоящие в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

.

В качестве критерия примем отношение большей исправленной дисперсии к меньшей, т. е. СВ F.

. (5.39)

Величина F при условии справедливости H₀ имеет распределение Фишера – Снедекора со степенями свободы

;

,

где n₁ – объём выборки, по которой вычислена большая исправленная дисперсия;

n₂ – объём выборки, по которой найдена меньшая дисперсия.

Критическую область строят в зависимости от вида конкурирующей гипотезы H₁.

Если , то строят правостороннюю критическую область. Критическую точкуF_кр находят по таблице распределения Фишера – Снедекора в зависимости от параметров ,k₁, k₂. Критическая область определяется неравенством F > F_кр, область принятия гипотезы – F < F_кр.

Если , то строят двустороннюю критическую область. Правую критическую точкуF_кр2 находят по таблице критических точек распределения Фишера – Снедекора в зависимости по параметров ,k₁, k₂.

Левых критических точек эта таблица не содержит. Однако для обеспечения надёжности критерия в двустороннюю критическую область F с уровнем значимости , правая критическая точка была определена с доверительной вероятностью. Поэтому критическая область удовлетворяет неравенствуF > F_кр2, область принятия гипотезы –

F < F_кр2.

Пример. По двум независимым выборкам, объекты которых соответсвенно равны n₁ =10 и n₂ = 15, извлечённым из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии и. Припроверитьпри

Решение.

Исходя из вида H₁, критическая область – двусторонняя. Определяем F_кр2 пр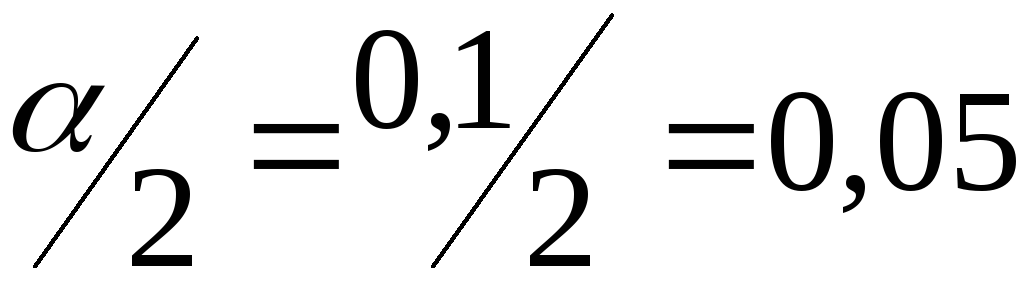и , и.

.

Вычисляем по (5.39) .

Т. к. , тоH₀ не опровергается, дисперсии можно считать равными.

5.3.4 Проверка статистической гипотезы о законе распределения

При проверке статистической гипотезы о законе распределения H₀ всегда формулируется следующим образом: генеральная совокупность распределена по закону, например, нормальному, а H₁: генеральная совокупность не распределена по закону, например, нормальному.

Выбор H₀ осуществляется, как правило, путём сравнения полигона и гистограммы выборки с графиками функций частных теоретических законов распределения.

Проверка H₀ проводится с использованием специально подобранной СВ, представляющей собой меру расхождения между эмпирическим и теоретическим распределениями, называмой в этом случае критерием согласия.

Критерии согласия не доказывают справедливость гипотезы, а лишь устанавливают для принятого значения её согласие или несогласие с данными наблюдений.

Имеется несколько примеров согласия: («хи квадрат»), Пирсона, Колмогорова, Смирнова и др.

Рассмотрим применение критерия Пирсона к проверке гипотезы о законе распределения генеральной совокупности.

Пусть из генеральной совокупности извлечена выборка объёмом n и получено статистическое распределение. Объём выборки должен быть достаточно велик ( ), частотыn_i , должны быть не менее 5.

В качестве критерия согласия Пирсона примем СВ

, (5.40)

где – теоретическая частота, частота, вычисленная в предположении закона распределения, сформулированного в H₀.

, (5.41)

где – вероятность наблюдаемого значения ДСВ X, вычисленная при допущении, что ДСВ X имеет распределение, сформулированное в H₀.

или – вероятность попадания НСВ X в i-й частичный интервал, вычисленная при допущении, что НСВ X имеет распределение, сформулированное в H₀.

Величина имеет распределение «хи квадрат» со степенями свободы

, (5.42)

где k – число вариант для ДСВ X или интервалов для НСВ X в выборочной совокупности;

d – число наложеных связей, число параметров, определённых по опытным данным. Для нормального распределнеия d=2, для показательного распределения d=1, для распределения Пуассона d=1.

Т. к. относторонний критерий более «жёстко» отвергает H₀, чем двусторонний, строим правостороннюю критическую область, для которой критическую точку определяем по таблице критических точек распределения по заданному и вычисленномуr.

Используя статистчиеское распределение, по формуле (5.40) вычисляем наблюдаемое значение критерия согласия Пирсона . Если – нет оснований отвергнуть H₀.

Если 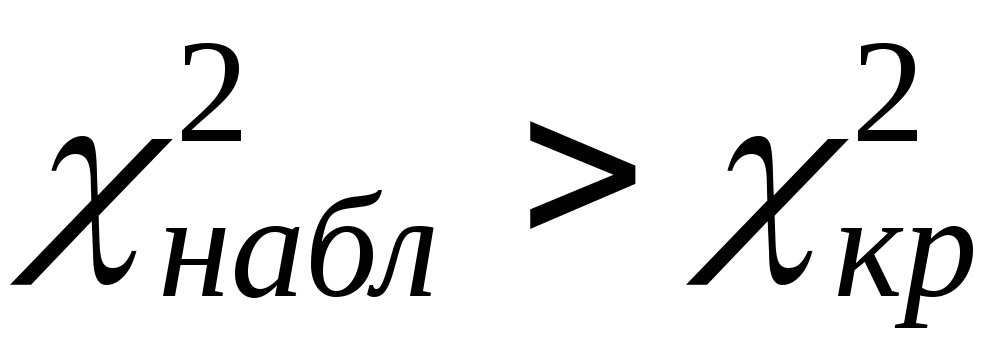– H₀ отвергают.

Пример. В. Е. Гмурман «Теория вероятностей и математическая статистика», стр. 332.