6.3 Выборочное корреляционное отношение (вко)

Для оценки тесноты нелинейной корреляции используются следующие характеристики:

- – выборочное корреляционное отношениеY к X;

- – выборочное корреляционное отношениеX к Y.

ВКО Y на X называют отношение межгруппового СКО к выборочному СКО величины Y , рассчитаным по выборочным данным

(6.8)

где межгрупповое СКО выборочное;

–СКО величины Y (общее СКО Y).

(6.9)

где n – объём выборки;

–частота варианты СВX;

–частота варианты СВY;

–выборочная средняя СВ Y (общая средняя Y);

–условная средняя СВ Y.

Условным средним называют среднее арифмитическое наблюдающихся значенийY, соответствующих ,.

Аналогично определяется ВКО X на Y:

(6.10)

Т. к. обладает теми же свойствами, что и, при перечислении свойств ВКО обозначим его.

Свойства ВКО:

1. ВКО удовлетворяет двойному неравенству

.

2. Если , тоX и Y не коррелированы.

3. Если , тоX и Y связаны функциональной зависимостью.

4. ВКО не меньше абсолютной величины r_в: .

5. Если ВКО равно абсолютной величине r_в, то имеет место точная линейная корреляционная зависимость, т. е. точки ,,…,лежат на прямой линии регрессии.

6. ВКО служит мерой тесноты связи любой формы, в том числе и линейной.

7. Элементы регрессионного анализа

Регрессионный анализ включает методы исследования корреляционной зависимости между случайными величинами, представленной уравнением регрессии.

7.1 Выборочные уравнения регрессии

В разделе 4.4 были введены уравнения регрессии Y на X и X на Y (4.25).

, .

Условное МО является функцией отx, следовательно, его оценка, т. е. условное среднее также функция отx. Обозначив эту функцию через , получим уравнение

, (7.1)

которое называют выборочным уравнением регрессии Y на X. Функцию называютвыборочной регрессией Y на X, а её график – выборочной линией регрессии Y на X.

Аналогично уравнение

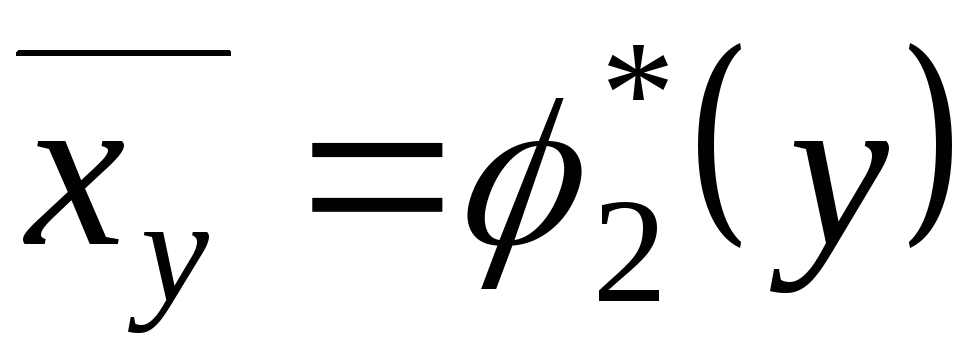(7.2)

называют выборочным уравнением регрессии X на Y; функцию – выборочной регрессией X на Y, а её график – выборочной линией регрессии X на Y.

Выборочное уравнение регрессии находять по выборке объёма n связанных пар наблюдений ,из совместной ГСX и Y.

7.2 Выборочное уравнение прямой линии регрессии

Рассмотрим выборочное уравнение прямой линии среднеквадратичной регрессии Y на X в виде

, (7.3)

где – угловой коэффициент прямой линии регрессии, который называютвыборочным коэффициентом регрессии Y на X; он является оценкой коэффициента регрессии (раздел 4.4).

Подберём параметры иb таким образом, чтобы точки ,,…,, построенные на плоскостиXоY, лежали как можно ближе к прямой (7.3).

При использовании метода наименьших квадратов (МНК) смысл этого требования интерпретируется так: сумма квадратов отклонений должна быть минимальной. Под отклонением понимают разность ,, где– вычисленная по уравнению (7.3) ордината наблюдаемого значения;– наблюдаемая ордината, соответствующая.

Запишем это требование в виде функции:

или

.

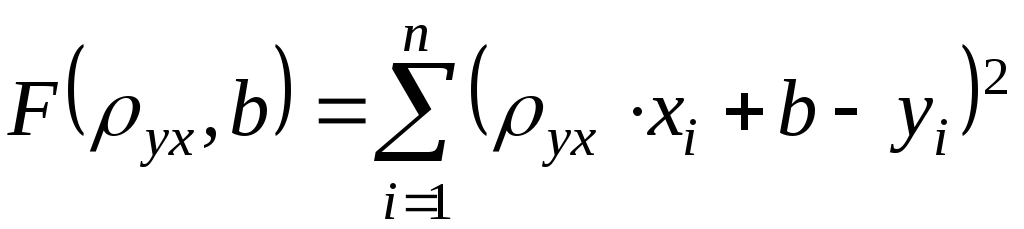Для отыскания минимума функции приравняем нулю соответствующие частные производные

;

.

Выполнив преобразования, получим систему

Решив данную систему, найдём искомые параметры

;

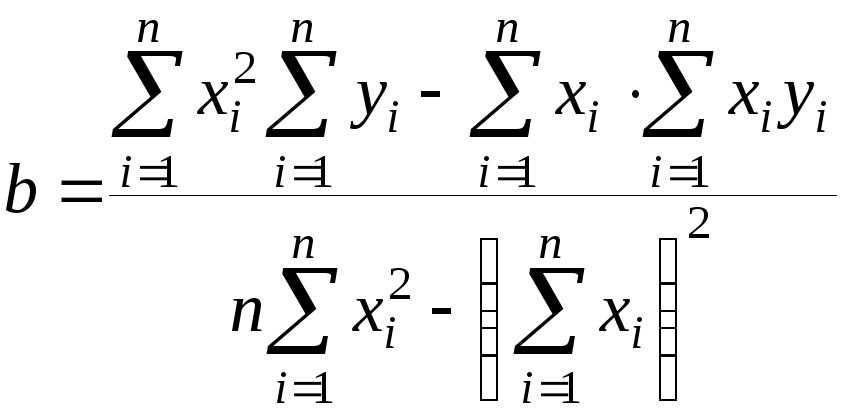. (7.4)

Аналогично можно найти выборочное уравнение прямой линии регрессии X на Y.

. (7.5)

Пример. Найти уравнение прямой линии регрессии по данным наблюдений:

X	1,00	1,50	3,00	4,50	5,00
Y	1,25	1,40	1,50	1,75	2,25

Составляем расчётную таблицу:

1,00	1,25	1,00	1,250
1,50	1,40	2,25	2,100
3,00	1,50	9,00	4,500
4,50	1,75	20,25	4,875
5,00	2,25	25,00	11,250

Находим неизвестные параметры из уравнения прямой линии регрессии:

;

.

Записываем искомое уравнение:

.

Если данные наблюдений представлены в виде корреляционнной таблицы 6.1, то можно вычислить по формуле

. (7.6)

Умножим обе части равенства (7.6) на дробь , получим формулу (6.3) для вычисленияr_в.

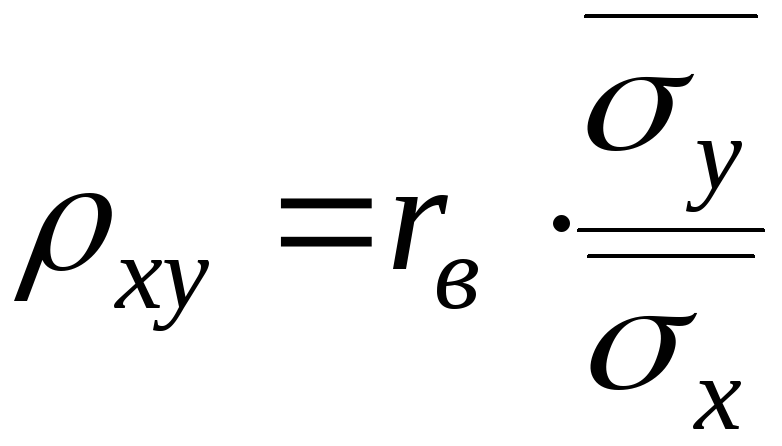. (7.7)

Отсюда уравнение (7.3) можно записать через r_в:

. (7.8)

Аналогично уравнение (7.5) примет вид

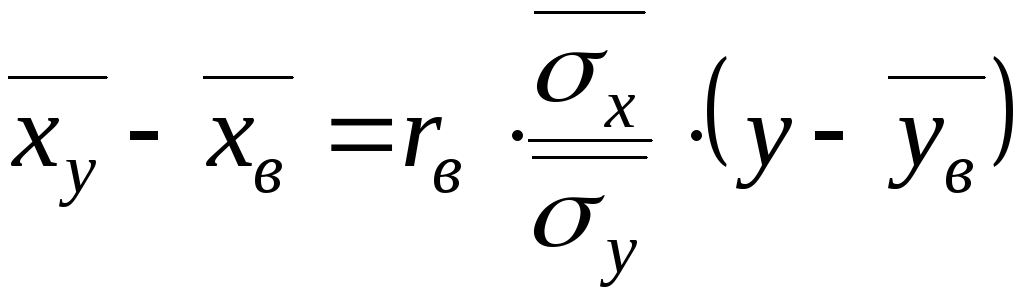. (7.9)