4. Система двух св (двумерная св)

4.1. Общие сведения

Система двух СВ – это совокупность двух СВ и, рассматриваемых совместно (как единое целое). Каждую из величин,называютсоставляющей (компонентой) двумерной СВ. Обозначают двумерную СВ , а возможные значения. Геометрически система двух СВинтерпретируется как случайная точка с координатамина плоскости.

Различают

• дискретные двумерные СВ (составляющие 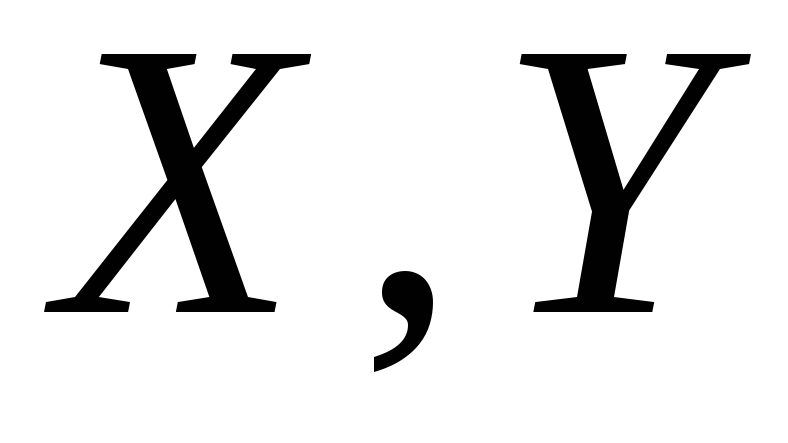- дискретны)

• непрерывные двумерные СВ (составляющие - непрерывны)

Система двух СВ может быть полностью представлена законом распределения, частично – числовыми характеристиками.

4.2. Закон распределения системы двух св

Законом распределения вероятностей двумерной СВ называют соответствие между возможными значениями СВ и их вероятностями.

Закон распределения двумерной СВ может быть задан

1. таблично;

2. интегральной функцией распределения;

3. дифференциальной функцией распределения (двумерной плотностью распределения).

Для дискретных двумерных СВ закон распределения имеет вид 1 или 2, для непрерывных – 2 или 3. Функция распределения – универсальный способ представления закона распределения системы двух СВ.

4.2.1 Табличное представление закона распределения двумерной св

Используется для дискретной двумерной СВ. Имеет вид таблицы с двойным входом, содержащей возможные значения и их вероятности,,

			…		…
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…

Т.к. события ,образуют полную группу, то сумма вероятностей, помещенных во все клетки равна 1.

Зная закон распределения дискретной двумерной СВ, можно найти законы распределения каждой из составляющих

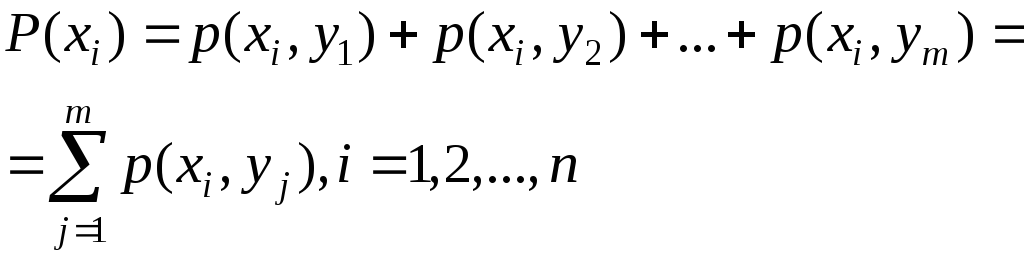
Аналогично

.

Пример. Найти законы распределения составляющих идля дискретной СВ, заданной таблично:

x y	2	3	4
0	0,2	0	0
0,1	0,05	0,1	0,15
0,2	0,1	0,15	0
0,3	0,05	0,15	0,05

Решение.

Закон распределения

	2	3	4
	0,4	0,4	0,2

Закон распределения

	0	0,1	0,2	0,3
	0,2	0,3	0,25	0,25

4.2.2 Интегральная функция распределения двумерной св

Интегральной функцией распределения двумерной СВ ()называют функцию , определяющую для каждой пары чиселивероятность того, чтопримет значение меньше, и при этомпримет значение меньше

. (4.1)

Другими словами - вероятность совместного выполнения двух неравенстви.

Геометрически есть вероятность попадания случайной точкив бесконечный квадрант с вершиной, расположенный левее и ниже этой вершины.

Свойства :

1. Значения удовлетворяют двойному неравенству

2. есть неубывающая функция по каждому аргументу, т.е.

если

если

3. Имеют место предельные соотношения

4. При становится интегральной функцией составляющей

При становится интегральной функцией составляющей

Используя можно определить вероятность попадания случайной точкив некоторую область.

Если вид области полуполоса

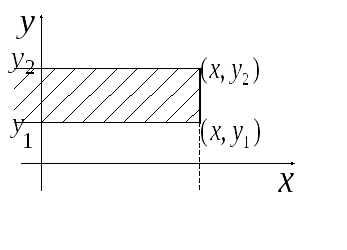
то вероятность попадания в неё (полуполосу) равна приращению по одному из аргументов

(4.2)

Если вид области – прямоугольник

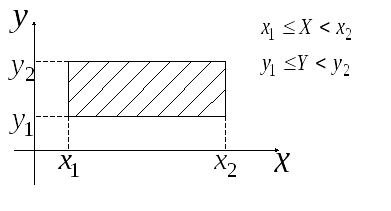
то вероятность попадания

(4.3)

Пример. Двумерная СВ задана

Найти вероятность того, что СВ примет значение из квадрата, вершины которого имеют координаты

Решение.

Множество точек заданного квадрата определяется соотношением

тогда

3. Дифференциальная функция распределения непрерывной двумерной СВ

Дифференциальная функция распределения непрерывной двумерной СВ (плотность распределения непрерывной двумерной СВ, двумерная плотность вероятностей) - это вторая смешанная производная от функции распределения

(4.4)

или (что следует из определения производной) - это предел отношения вероятности попадания случайной точки в элементарный участок плоскости, примыкающий к точке, к площади этого участка, когда его размеры стремятся к нулю.

Поверхность, изображающая функцию называетсяповерхностью распределения.

Интегральная функция выражается черезформулой

(4.5)

Величина называетсяэлементом вероятности для системы двух СВ и равна вероятности попадания случайной точки в элементарный прямоугольник со сторонами,, примыкающий к точке.

Вероятность попадания случайной точки в произвольную областьопределяется формулой

(4.6)

Для прямоугольной области

Свойства :

1. есть неотрицательная функция.

2. Двойной несобственный интеграл с бесконечными пределами от равен 1

Если все возможные значения принадлежат конечной области, то

Плотности отдельных величин, входящих в систему двух СВ, можно вычислить через совместную плотность

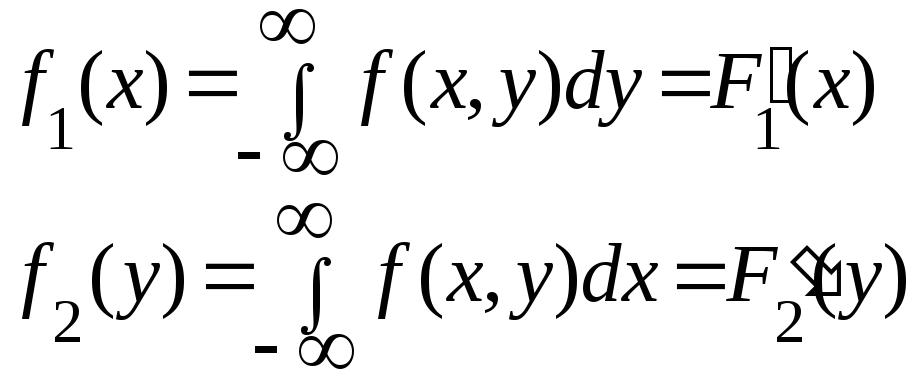(4.7)

Пример. Система двух СВ подчинена закону распределения с плотностью

Найти коэффициент ,, вероятность попадания случайной точкив квадрат, центр которого совпадает с началом координат, а стороны имеют длину равную 2.

Решение.

Из условия находим

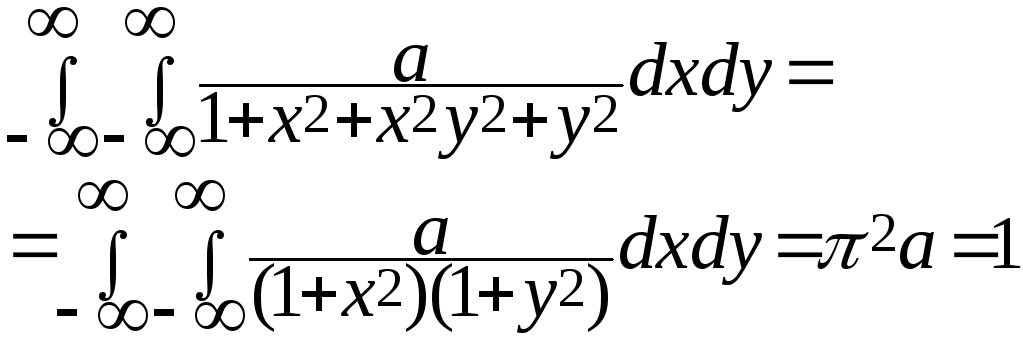
Из формулы (4.5)

По (4.6)