5.1.3 Числовые характеристики выборки

Числовые характеристики выборки – параметры выборки, выражающие наиболее существенные особенности статистического распределения выборки.

Выборочной средней называют среднее арифмитическое значение признака выборочной совокупности.

(5.4)

Если статистическое распределение выборки задано интервальным вариационным рядом, тогда при вычислении необходимо перейти к дискретному вариационному ряду, вариантами которого выступают середины интервалов

(5.5)

Модой Мо называют варианту, которая имеет наибольшую частоту.

Для интервального статистического распределения сначала определяют модальный интервал [x_m; x_m+1), для которого ,

где h_i – длина частичного интервала [x_i; x_i+1),

n_i – число вариант этого интервала.

Далее

(5.6)

Медианой Ме дискретного статистического распределения называют варианту, которая делит вариационный ряд на две части, равных по числу вариант.

Если число вариант нечётное, то ,

если чётное, то

(5.7)

Медианой M_e интервального статистического распределения называется число, для которого выполняется равенство

.

Формула для вычисления M_e имеет вид

,

(5.8)

где [x_m; x_m+1) – медианный частичный интервал, для которого выполняется неравенство

и .

Дисперсия выборки (выборочная дисперссия) D_в – среднее арифмитическое квадратов отклонений наблюдаемых значений признака от их среднего значения .

. (5.9)

Вычисление D_в можно упростить, используя следующую формулу

. (5.10)

D_в характеризует рассеяние наблюдаемых значений количественного признака вокруг своего среднего значения .

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень изD_в.

. (5.11)

Размахом варьирования R называют разность между наибольшей и наименьшей вариантами.

. (5.12)

Размах варьирования является простейшей характеристикой рассеяния вариационного ряда.

Средним абсолютным отклонением называют среднее арифметическое абсолютных отклонений

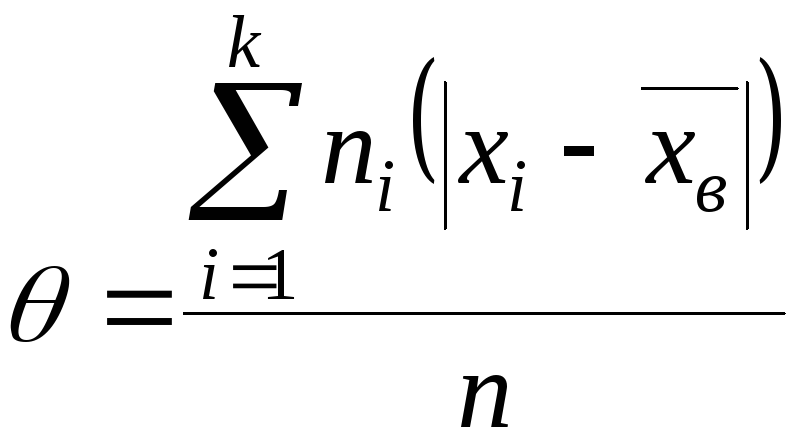. (5.13)

Среднее абсолютное значение используется для характеристики рассеяния вариационного ряда.

Коэффициентом вариации V называют выраженное в процентах отношение к.

(5.14)

где .

Коэффициент вариации V служит для сравнения величин рассеяния по отношению к двух вариационных рядов, даже если варианты имеют различную размерность.

Сводными характеристиками статистических распределений выступают статистические (эмпирические) моменты.

Обычным эмпирическим моментом порядка l называют среднее значение l-х степеней разностей .

, (5.15)

где с – произвольная постоянное число, т. н. ложный нуль.

Начальным эмпирическим моментом порядка l называют обычный момент порядка l при с=0.

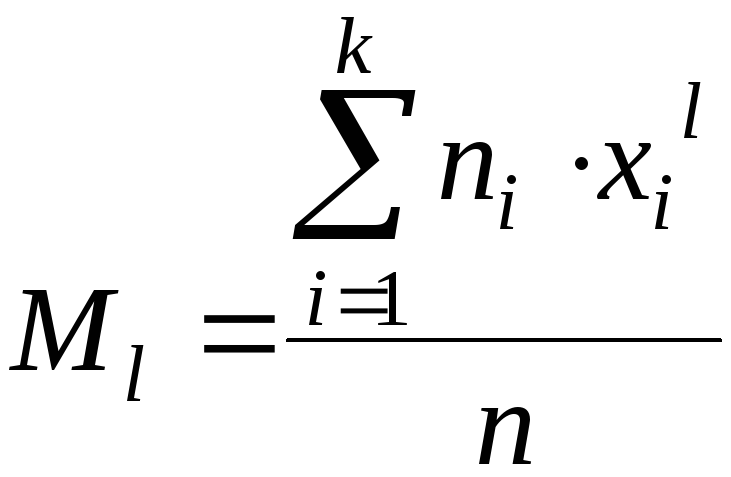. (5.16)

В частности

,

т. е. начальный эмпирический момент первого порядка равен выборочной средней.

Центральным эмпирическим моментом порядка l называют обычный момент порядка l при .

. (5.17)

В частности

,

т. е. центральный эмпирический момент второго порядка равен выборочной дисперсии.

Центральные моменты можно выразить через обычные:

;

; (5.18)

.

Условным эмпирическим моментом порядка l называют начальный момент порядка l, вычисленный для условных вариант.

, (5.19)

где u_i – условная варианта.

Условными называют варианты, определяемые равенством

, (5.20)

где с – любая варианта x_i, которая располагается в середине вариационного ряда или является модой;

h – шаг, т. е.

.

Таким образом, для вариационного ряда, состоящего из равноотстоящих вариант с шагом h, условные варианты есть целые числа.

В частности

Отсюда

. (5.21)

Выразим обычные моменты через условные:

.

Тогда

. (5.22)

Подставив (5.22) в (5.18), можно получить удобные для вычислений формулы, выражающие центральные моменты через условные.

Например, для m₂:

. (5.23)

Пример. Для статистического распределения рассчитать числовые характеристики.

xi	2	6	10
ni	12	18	30

Решение.

.

.

.

Или

.

.

.

.

.

Перейдём к условным вариантам.

с=10.

ui	-2	-1	0
ni	12	18	30

.

.

.

.