3.5 Непрерывные св

Непрерывной СВ в широком смысле называется СВ, которая может принимать все (бесконечно много) значения из некоторого конечного или бесконечного промежутка. Если функция распределения везде непрерывна и имеет производную, СВназываетсянепрерывной в узком смысле.

Пример:

1. Координаты точки попадания при выстреле.

2. Время опоздания поезда.

3. Время безотказной работы лампы.

3.5.1. Формы представления закона распределения нсв

Ряд распределения, многоугольник распределения и формула не используются в качестве закона распределения НСВ.

Функция распределения НСВ , есть непрерывная, кусочно-дифференцируема функция с непрерывной производной.

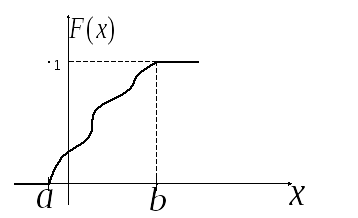
График функции распределения НСВ , которая принимает все возможные значения на интервале.

Из свойства 2 функции распределения вытекает важное следствие для НСВ: вероятность того, что НСВ примет одно определенное значение равна 0. И тогда

Таким образом, не представляет интереса говорить о вероятности того, что НСВ примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малой.

При этом надо понимать, что не означает, что событие невозможно. В результате испытания НСВ обязательно примет одно из возможных значений, в том числе и.

Плотность вероятностей (плотность распределения вероятностей, плотность) НСВ - функция, определяемая как первая производная функции распределения

(3.12)

Из определения следует, что - есть первообразнаяи выражается черезформулой.

(3.13)

Геометрически есть площадь кривой распределения, лежащая левее точки.

График называетсякривой распределения.

Размерность обратна размерности СВ (это не вероятность).

Свойства :

1. неотрицательная функция, т.е.

2.Несобственный интеграл от на интервалеравен 1.

(3.14)

Это так называемое условие нормировки плотности распределения.

Если все возможные значения НСВ принадлежат интервалу, то

(3.15)

3. Вероятность того, что НСВ 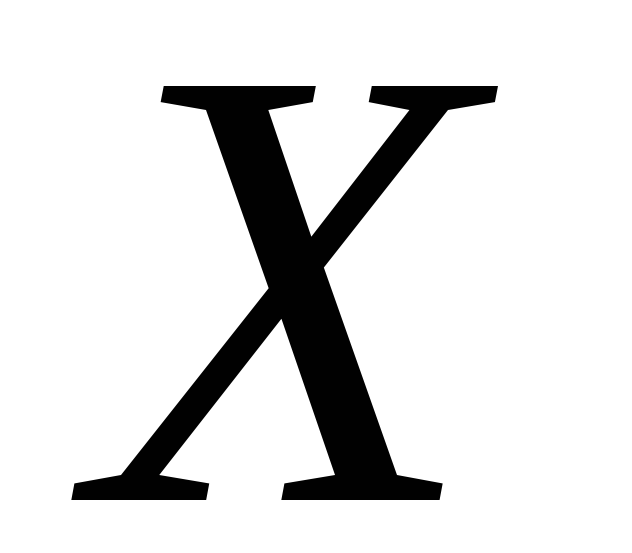примет значение из интервала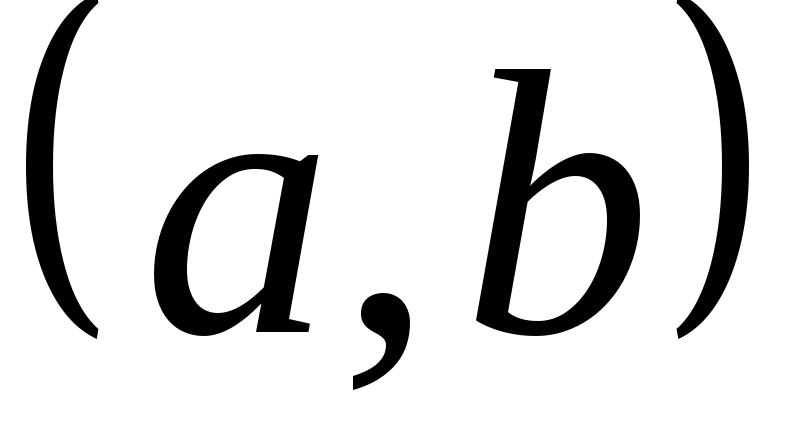равна определенному интегралу от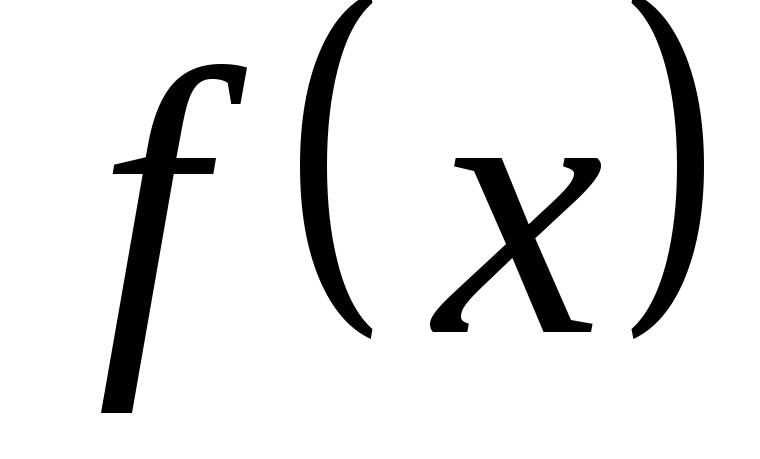, взятому на интервале

(3.16)

Геометрически это означает, что есть площадь под кривой распределения, ограниченная линиямиислева и справа соответственно и осью абсцисс внизу.

Величина для НСВ называетсяэлементом вероятности и приближенно равна вероятности попадания СВ на элементарный отрезок, примыкающий к точке.

(3.17)

Пример. Для НСВ , плотность распределения которой имеет вид

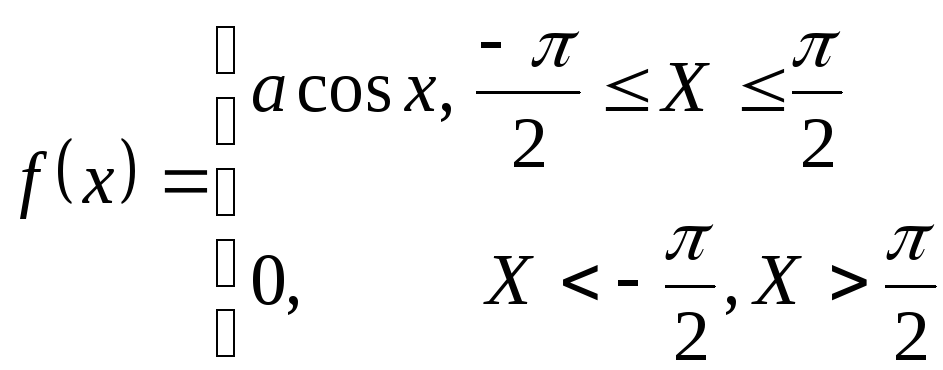
1. Определить коэффициент ;

2. Построить кривую распределения;

3. Найти и построить её график;

4. Вычислить

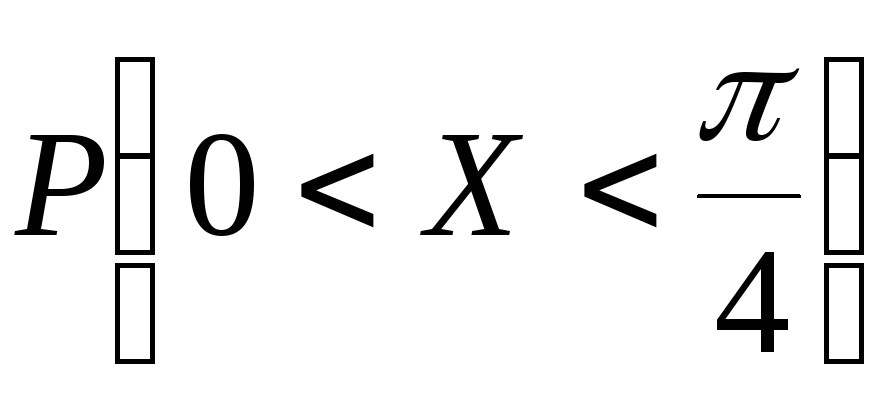
Решение:

1. По (3.14)

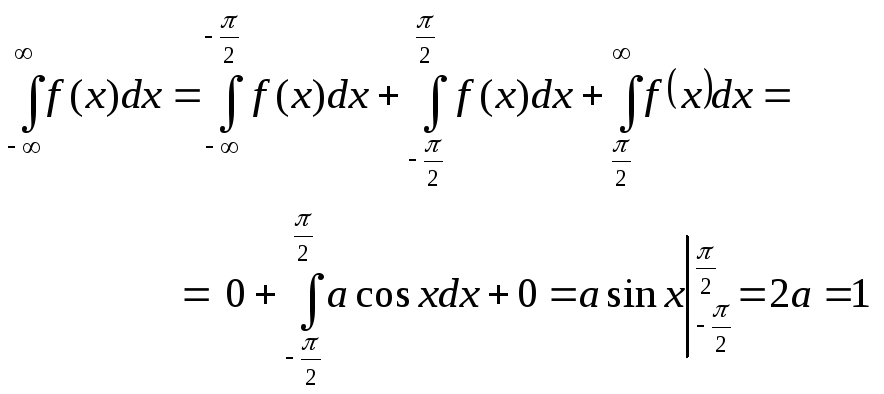
2. Кривая распределения

3. По (3.13)

При

При

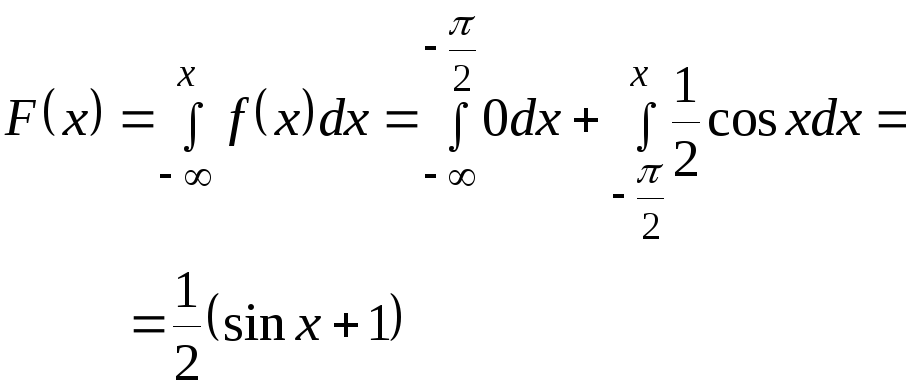
При

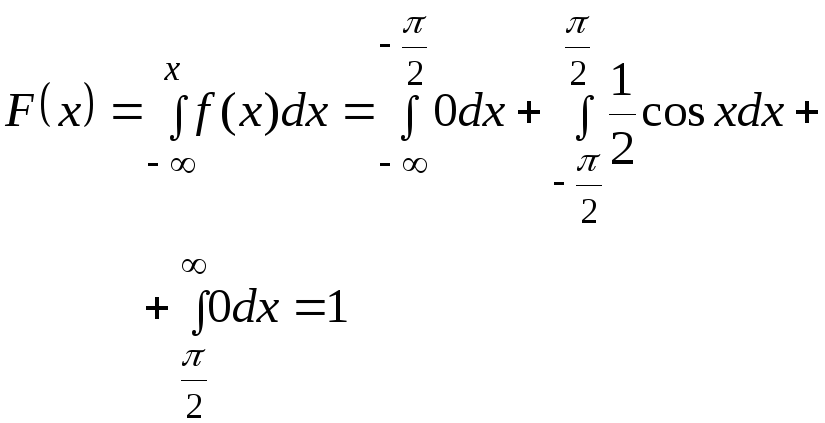
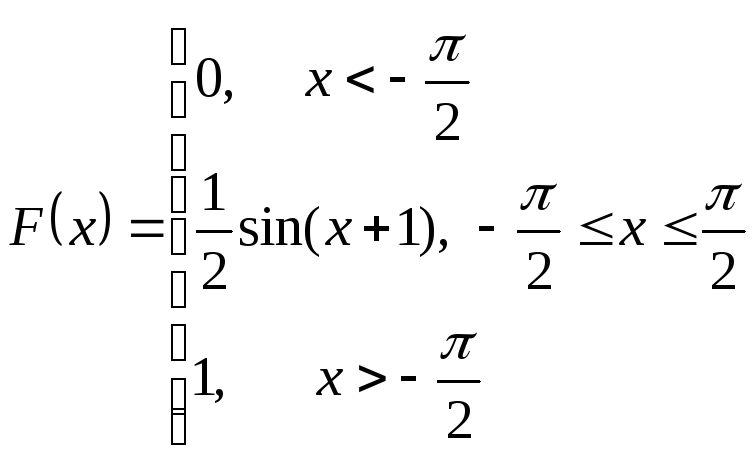
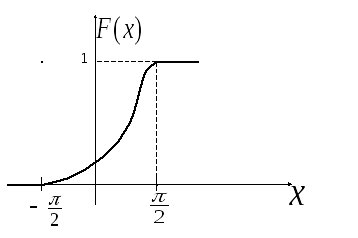
График функции

4. Согласно второго свойства

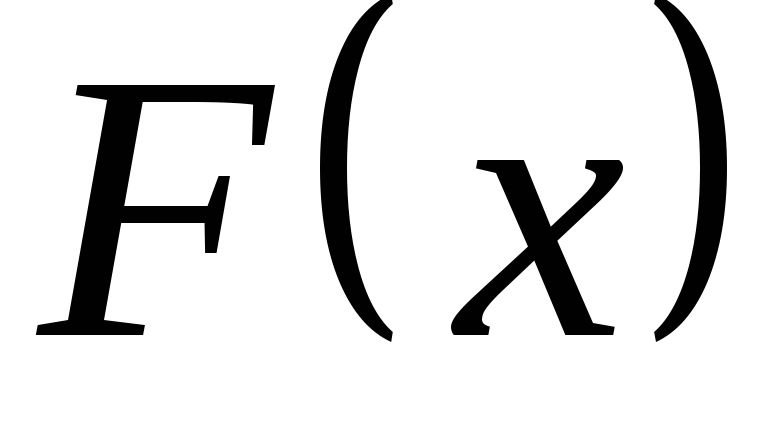
3.5.2 Числовые характеристики нсв

Математическое ожидание НСВ с плотностью- среднее значение НСВ, вычисляемое по формуле

(3.18)

или

(3.19)

Если НСВ принимает значение только из интервала.

Мода НСВ значение , в которойимеет максимум.

Медиана НСВ геометрически – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.

Дисперсия НСВ

(3.20)

или

(3.21)

СКО НСВ

(3.22)

Начальный теоретический момент

-го порядка НСВ :

, (3.23)

Центральный теоретический момент

-го порядка НСВ :

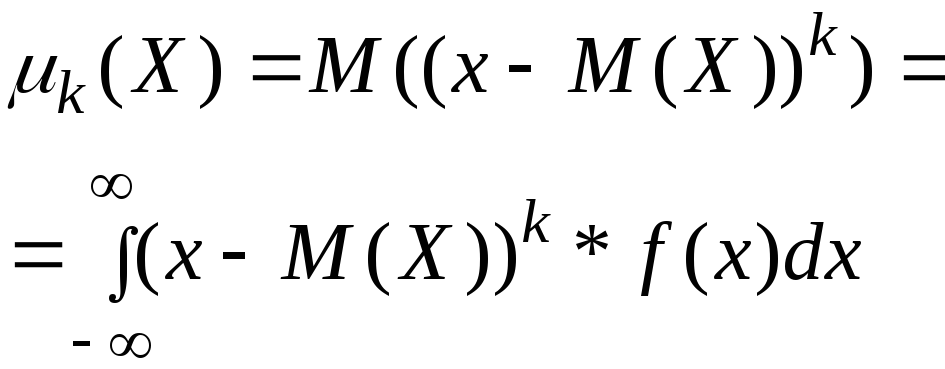(3.24)

Пример. Для НСВ , функция распределения которой имеет вид:

Найти числовые характеристики

, ,,.

Решение:

1. По (3.12) определим

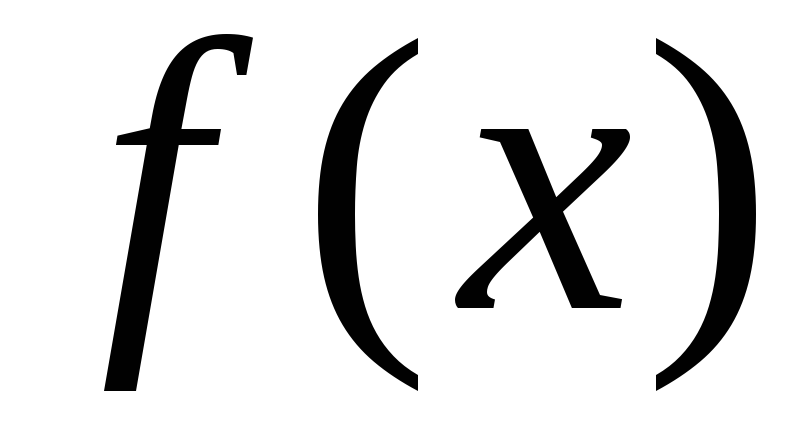
при ,

при ,

при ,

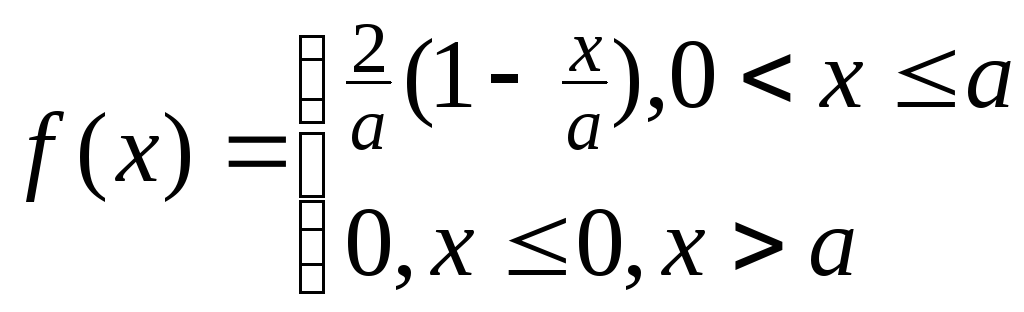
2. По (3.19)

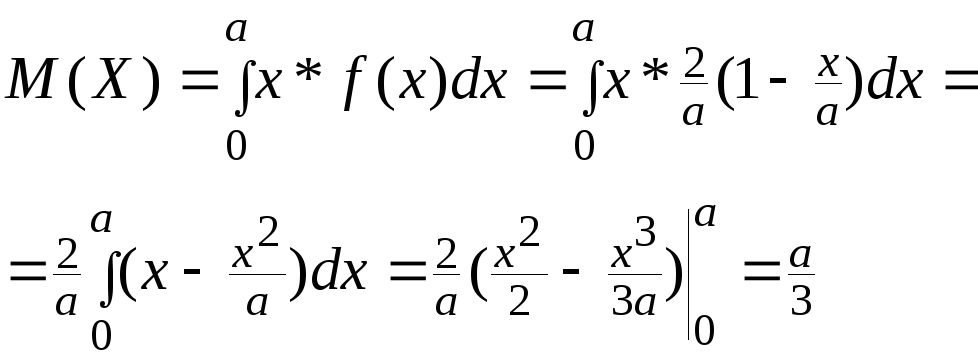
3. По (3.21)

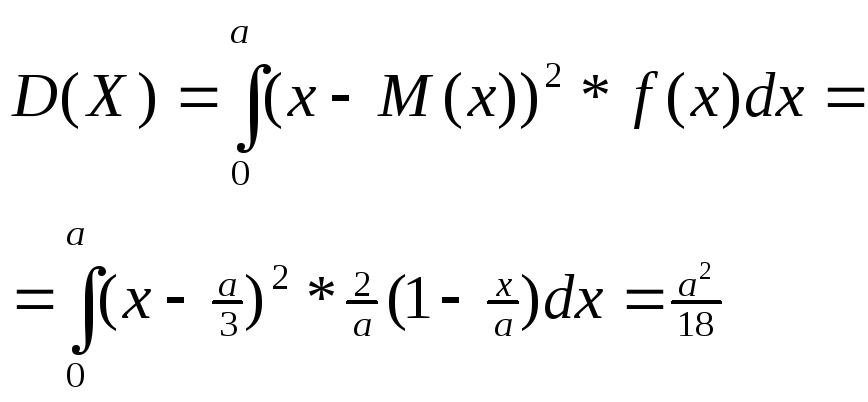
4. По (3.22)

5.