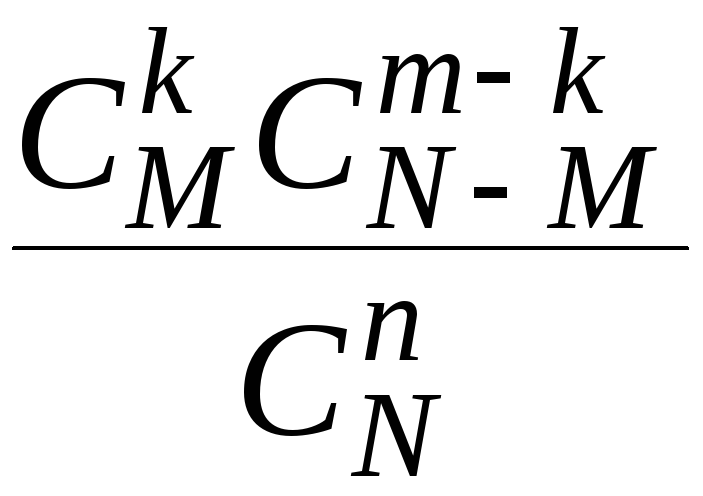- •«Спеціальні розділи математики»
- •«Теорія ймовірностей і математична статистика»
- •Специальные разделы метематики
- •1.4.2 Правила комбинаторики
- •2 Основные теоремы теории вероятностей
- •2.1 Теорема умножения вероятностей
- •2.4 Следствия теорем сложения и умножения
- •2.4.1 Теорема о вероятности появления хотя бы одного события
- •2.4.2 Формула полной вероятности
- •3 Случайные величины
- •3.1 Общие сведения
- •3.2 Функция распределения случайной величины.
- •3.4.1 Формы закона распределения дискретной случайной величины
- •3.4.2 Числовые характеристики дсв
- •3.4.3 Основные (типовые) распределения дсв.
- •3.5 Непрерывные св
- •3.5.1. Формы представления закона распределения нсв
- •3.5.2 Числовые характеристики нсв
- •3.5.3 Основные (типовые) законы распределения нсв
- •4. Система двух св (двумерная св)
- •4.1. Общие сведения
- •4.2. Закон распределения системы двух св
- •4.2.1 Табличное представление закона распределения двумерной св
- •4.2.2 Интегральная функция распределения двумерной св
- •Числовые характеристики системы двух св
- •Зависимые и независимые св
- •Часть II Математическая статистика
- •5. Элементы математической статистики
- •5.1 Теория выборок
- •5.1.1 Способы формирования выборки
- •5.1.2 Статистическое распределение выбоки
- •5.1.3 Числовые характеристики выборки
- •5.2 Теория оценок
- •5.2.1. Точечные оценки.
- •5.2.2 Интервальные оценки
- •5.3 Теория проверки статистических гипотез
- •5.3.1 Виды статистических гипотез
- •5.3.2 Статистический критерий
- •5.3.3 Проверка статистической гипотезы о параметрах распределения
- •5.3.4 Проверка статистической гипотезы о законе распределения
- •6 Элементы корреляционного анализа
- •6.1 Корреляционное поле
- •6.2 Выборочный коэффициент корреляции
- •6.3 Выборочное корреляционное отношение (вко)
- •7. Элементы регрессионного анализа
- •7.1 Выборочные уравнения регрессии
- •7.2 Выборочное уравнение прямой линии регрессии
- •7.3 Выборочное уравнение нелинейной регрессии
- •8. Элементы дисперсионного анализа
- •8.1 Общие сведения
- •8.2 Общая, факторная и остаточная суммы квадратов отклонений.
- •8.3 Общая, факторная и остаточная дисперсии.
- •8.4 Применение метода дисперсионного анализа
3.4.3 Основные (типовые) распределения дсв.
СВ
![]() называется распределенной
по биномиальному
закону,
если её возможные значения
называется распределенной
по биномиальному
закону,
если её возможные значения
![]() ,
а соответствующие вероятности
рассчитываются по формуле Бернулли
(2.22)
,
а соответствующие вероятности
рассчитываются по формуле Бернулли
(2.22)
![]()
![]()
![]() -
число появления события в
-
число появления события в
![]() независимых испытаниях.
независимых испытаниях.
Биномиальное
распределение зависит от двух параметров
![]() и
и![]() .
.
Ряд распределения имеет вид:
|
|
0 |
1 |
2 |
… |
|
|
|
|
|
|
|
|
![]()
![]()
![]() (3.7)
(3.7)
Пример. Проверить формулы (3.7) для примера рассмотренного выше.
Решение.
![]() ,
,
![]() ,
,![]()
![]()
![]()
ДСВ
![]() называетсяраспределенной
по закону Пуассона, если
её возможные значения
называетсяраспределенной
по закону Пуассона, если
её возможные значения
![]() ,
а соответствующие вероятности выражаются
формулой Пуассона
(2.24)
,
а соответствующие вероятности выражаются
формулой Пуассона
(2.24)
![]()
Распределение
Пуассона зависит от одного параметра
![]() -
среднее число появления событий при
-
среднее число появления событий при![]() испытаниях.
испытаниях.
Ряд распределения имеет вид:
|
|
0 |
1 |
2 |
… |
|
|
|
|
|
|
|
|
![]() (3.8)
(3.8)
Пуассоновское
распределение является предельным для
биномиального при
![]() ,
,![]() ,
если
,
если![]() .
.
Пример:
Устройство имеет 1000 элементов, которые работают независимо один от другого. Вероятность того, что элемент выйдет из строя во время работы
 .
Определить среднее количество элементов,
которые могут выйти из строя.
.
Определить среднее количество элементов,
которые могут выйти из строя.
Решение.
![]()
На АТС на протяжении часа поступает в среднем 30 вызовов. Найти вероятность того, что на протяжении минуты поступит не более 2-х вызовов.
Решение.
![]() -
среднее число
-
среднее число
вызовов за одну минуту
![]()
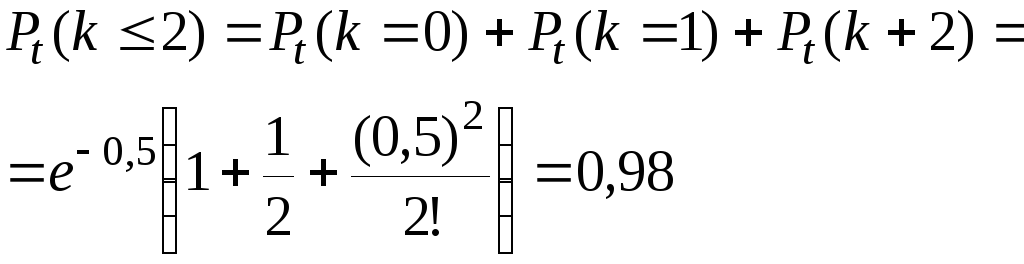
ДСВ
![]() называется распределенной погипергеометрическому
закону, если
её возможные значения
называется распределенной погипергеометрическому
закону, если
её возможные значения
![]() ,
а соответствующие вероятности определяются
гипергеометрической формулой
(1.7).
,
а соответствующие вероятности определяются
гипергеометрической формулой
(1.7).
 ,
,
![]()
Гипергеометрическое
распределение зависит от трех параметров
![]() .
.
Ряд распределения имеет вид:
|
|
0 |
1 |
2 |
… |
|
|
|
|
|
|
|
|
![]()
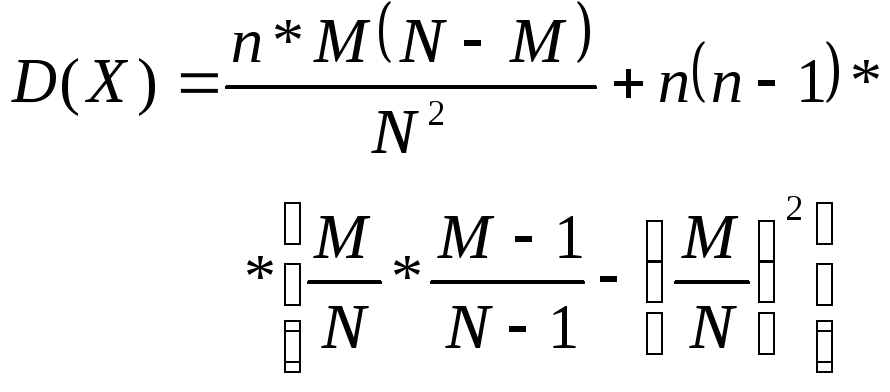 (3.9)
(3.9)
При
![]() гипергеометрическое распределение
дает вероятности, близкиек
вероятностям, найденным по биномиальному
закону.
гипергеометрическое распределение
дает вероятности, близкиек
вероятностям, найденным по биномиальному
закону.
Пример. В ящике имеется 10 однотипных деталей, из них 7 стандартных. Из ящика берут 4 детали. Построить ряд распределения ДСВ – числа стандартных деталей среди отобранных.
Решение.
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
ДСВ
![]() называется распределеннойпо
равномерному
закону, если ее возможные значения
называется распределеннойпо
равномерному
закону, если ее возможные значения
![]() ,
а соответствующие им вероятности можно
рассчитать
по формуле
,
а соответствующие им вероятности можно
рассчитать
по формуле
![]() ,
,
![]() .
.
Равномерное
распределение зависит от одного параметра
![]() .
.
Ряд распределения имеет вид:
|
|
0 |
1 |
… |
|
|
|
|
|
… |
|
![]() ,
,
![]()
Пример. На связке 5 ключей, из которых только один подходит к замку. Составить ряд распределения ДСВ числа ключей, которые пробуются для открытия замка.
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
![]()
![]()
![]()
![]()
![]()
ДСВ
![]() имеетгеометрическое
распределение,
если ее возможные значения
имеетгеометрическое
распределение,
если ее возможные значения
![]() а вероятности этих значений
а вероятности этих значений![]() .
.
Вероятности
![]() для ряда последовательных значений
для ряда последовательных значений![]() образуют бесконечно убывающую
геометрическую прогрессию со знаменателем
образуют бесконечно убывающую
геометрическую прогрессию со знаменателем![]() .
.
Ряд распределения имеет вид:
-
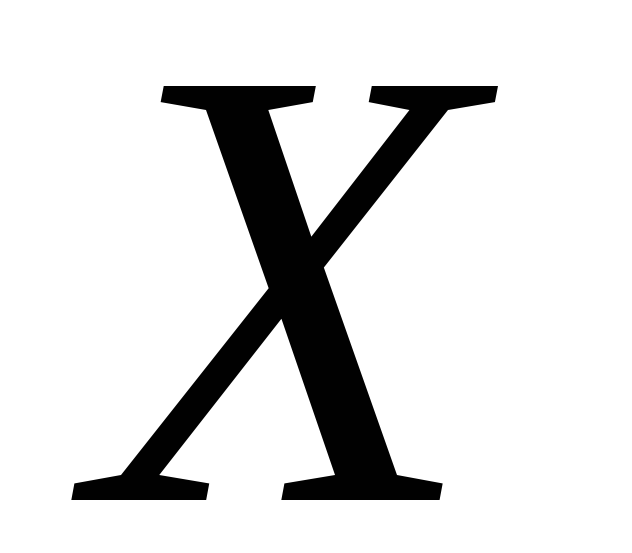
0
1
2
…

…
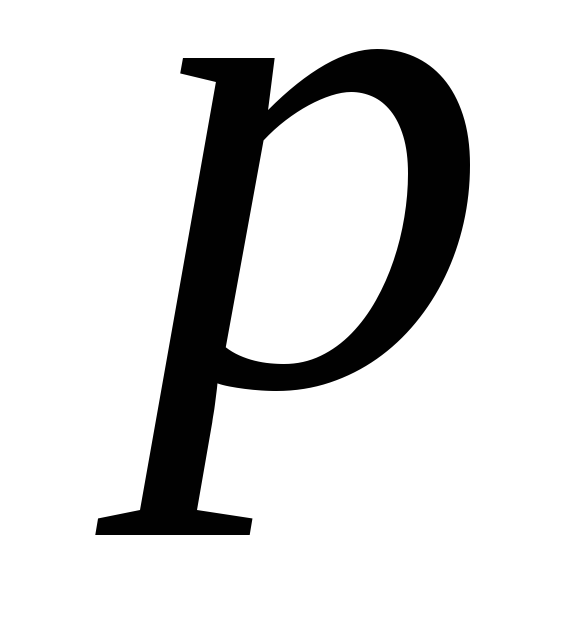


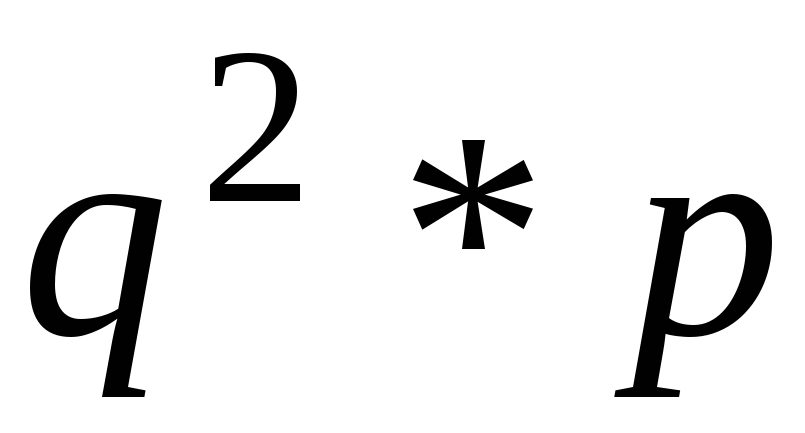
…

…
![]() ,
,
![]() (3.10)
(3.10)
Нередко
рассматривают СВ
![]() ,
равную числу попыток до получения
результата, включая удавшуюся попытку,
т.н. геометрическое распределение
начинающееся
с «1», для которого
,
равную числу попыток до получения
результата, включая удавшуюся попытку,
т.н. геометрическое распределение
начинающееся
с «1», для которого
![]()
Ряд
распределения СВ
![]() :
:
-

1
2
…
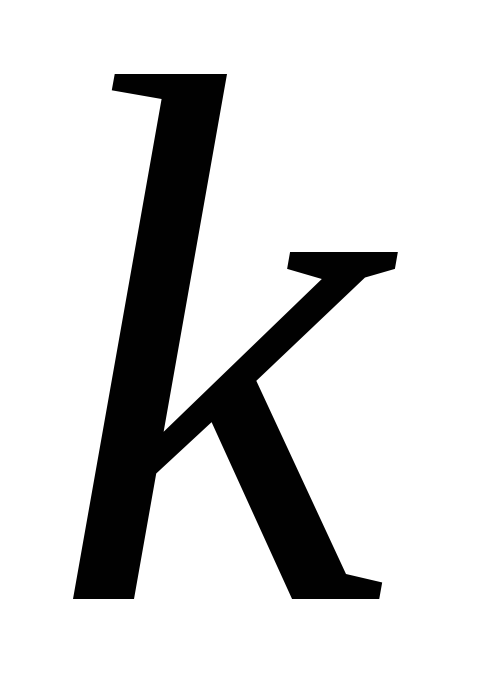
…


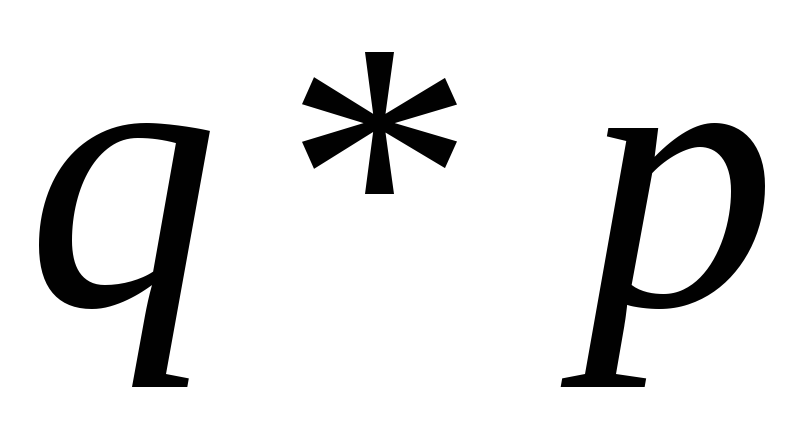
…
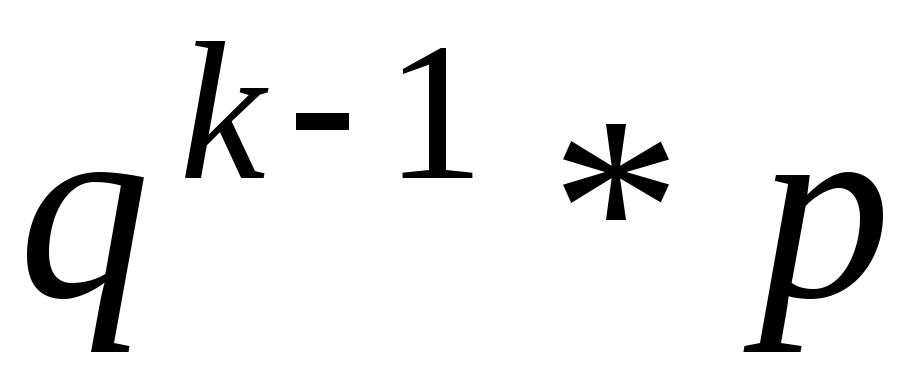
…
![]() ,
,
![]() (3.11)
(3.11)
Геометрическое
распределение зависит от одного параметра
![]() .
.
Пример.
Из корзины, в котором 3 черных и два белых
шара последовательно вынимают шары до
появления белого. Перед очередным
извлечением шара, вынутый ранее шар
возвращается в корзину. Построить ряд
распределения ДСВ
![]() - числа вынутых белых шаров до появления
черного и ДСВ
- числа вынутых белых шаров до появления
черного и ДСВ![]() - количество попыток до появления черного
шара.
- количество попыток до появления черного
шара.
Решение:
|
|
0 |
1 |
2 |
… |
|
|
|
|
|
… |
|
|
1 |
2 |
3 |
… |
|
|
|
|
|
… |