
- •«Спеціальні розділи математики»
- •«Теорія ймовірностей і математична статистика»
- •Специальные разделы метематики
- •1.4.2 Правила комбинаторики
- •2 Основные теоремы теории вероятностей
- •2.1 Теорема умножения вероятностей
- •2.4 Следствия теорем сложения и умножения
- •2.4.1 Теорема о вероятности появления хотя бы одного события
- •2.4.2 Формула полной вероятности
- •3 Случайные величины
- •3.1 Общие сведения
- •3.2 Функция распределения случайной величины.
- •3.4.1 Формы закона распределения дискретной случайной величины
- •3.4.2 Числовые характеристики дсв
- •3.4.3 Основные (типовые) распределения дсв.
- •3.5 Непрерывные св
- •3.5.1. Формы представления закона распределения нсв
- •3.5.2 Числовые характеристики нсв
- •3.5.3 Основные (типовые) законы распределения нсв
- •4. Система двух св (двумерная св)
- •4.1. Общие сведения
- •4.2. Закон распределения системы двух св
- •4.2.1 Табличное представление закона распределения двумерной св
- •4.2.2 Интегральная функция распределения двумерной св
- •Числовые характеристики системы двух св
- •Зависимые и независимые св
- •Часть II Математическая статистика
- •5. Элементы математической статистики
- •5.1 Теория выборок
- •5.1.1 Способы формирования выборки
- •5.1.2 Статистическое распределение выбоки
- •5.1.3 Числовые характеристики выборки
- •5.2 Теория оценок
- •5.2.1. Точечные оценки.
- •5.2.2 Интервальные оценки
- •5.3 Теория проверки статистических гипотез
- •5.3.1 Виды статистических гипотез
- •5.3.2 Статистический критерий
- •5.3.3 Проверка статистической гипотезы о параметрах распределения
- •5.3.4 Проверка статистической гипотезы о законе распределения
- •6 Элементы корреляционного анализа
- •6.1 Корреляционное поле
- •6.2 Выборочный коэффициент корреляции
- •6.3 Выборочное корреляционное отношение (вко)
- •7. Элементы регрессионного анализа
- •7.1 Выборочные уравнения регрессии
- •7.2 Выборочное уравнение прямой линии регрессии
- •7.3 Выборочное уравнение нелинейной регрессии
- •8. Элементы дисперсионного анализа
- •8.1 Общие сведения
- •8.2 Общая, факторная и остаточная суммы квадратов отклонений.
- •8.3 Общая, факторная и остаточная дисперсии.
- •8.4 Применение метода дисперсионного анализа
2 Основные теоремы теории вероятностей
2.1 Теорема умножения вероятностей
Произведением
двух событий
![]() и
и![]() называется
событие
называется
событие
![]() ,
состоящее в совместном появлении событий
,
состоящее в совместном появлении событий
![]() и
и
![]() .
.
Произведением
нескольких событий
![]() ,
,![]() ,…
,…![]() называется
событие
называется
событие
![]() ,
состоящее в совместном появлении всех
этих событий.
,
состоящее в совместном появлении всех
этих событий.
Пример:
Если событие
 - появление туза при вынимании карты
из колоды, событие
- появление туза при вынимании карты
из колоды, событие - появление карты бубновой масти, то
событие
- появление карты бубновой масти, то
событие есть появление туза бубновой масти.
есть появление туза бубновой масти.Если по мишени производится три выстрела и рассматриваются события
 - промах при первом выстреле,
- промах при первом выстреле, -
промах при втором выстреле,
-
промах при втором выстреле, - промах при третьем выстреле, то событие
- промах при третьем выстреле, то событие состоит в том, что в мишень не будет ни
одного попадания.
состоит в том, что в мишень не будет ни
одного попадания.
Теорема умножения 1
Вероятность
произведения двух событий
![]() и
и![]() равна произведению вероятности одного
из них на условную вероятность другого,
вычисленную в предположении, что первое
событие уже наступило
равна произведению вероятности одного
из них на условную вероятность другого,
вычисленную в предположении, что первое
событие уже наступило
![]() , (2.1)
, (2.1)
если
в качестве первого события взять
![]()
![]() ,
(2.2)
,
(2.2)
если
в качестве первого события взять
![]() .
.
![]() ,
,
![]() - условные вероятности событий
- условные вероятности событий![]() и
и![]() соответственно.
соответственно.
Условной
вероятностью
![]() называется
вероятность события
называется
вероятность события
![]() ,
вычисленную в предположении, что событие
,
вычисленную в предположении, что событие![]() уже наступило.
уже наступило.
Пример.
Студент знает 20 билетов из 30. Он тянет
билет шестым. Найти вероятность того,
что он сдаст экзамен (событие
![]() ),
если первых 5 человек вытащили 5 известных
ему билетов (событие
),
если первых 5 человек вытащили 5 известных
ему билетов (событие![]() ).
).
Решение.
![]()
![]()
Из формулы (2.1) можно получить формулу для вычисления условной вероятности
![]() (2.3)
(2.3)
Формула
(2.3) может быть использована при условии
![]() .
.
Пример. Проверить формулу (2.3) для предыдущего примера.
![]() находим
по (1.7) при
находим
по (1.7) при
![]() ,
,![]() ,
,![]() ,
,![]() .
.
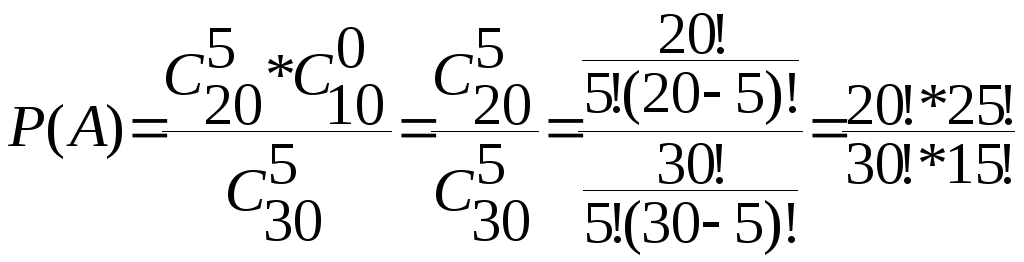
![]() определяем
по (1.7) при
определяем
по (1.7) при
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
![]()
Два
события
![]() и
и![]() называютсянезависимыми,
если появление одного из них не меняет
вероятности появления другого, т.е.
условная вероятность события
называютсянезависимыми,
если появление одного из них не меняет
вероятности появления другого, т.е.
условная вероятность события
![]() равна его безусловной вероятности или,
условная вероятность события
равна его безусловной вероятности или,
условная вероятность события![]() равна его безусловной вероятности
равна его безусловной вероятности
![]() (2.4)
(2.4)
![]() .
.
Если
событие
![]() не зависит от события
не зависит от события![]() ,
то и событие
,
то и событие![]() не зависит от события
не зависит от события![]() .
.
Два
события
![]() и
и![]() являютсязависимыми,
если
являютсязависимыми,
если
![]() или
или
![]() (2.5)
(2.5)
Если
событие
![]() зависит от события
зависит от события![]() ,
то и событие
,
то и событие![]() зависит от события
зависит от события![]() .
.
Пример. Из полной колоды карт (52 листа) вынимается одна карта. Рассматриваются события
![]() -
появление туза;
-
появление туза;
![]() -
появление карты красной масти;
-
появление карты красной масти;
![]() -
появление бубнового туза;
-
появление бубнового туза;
![]() -
появление десятки.
-
появление десятки.
Зависимы
или независимы пары событий
![]() и
и![]() ,
,![]() и
и![]() ,
,![]() и
и![]() ?
?
Решение.
Для
пары
![]() и
и![]()
![]()
![]()
![]()
![]()
![]()
![]()
справедливо
условие (2.4). Значит
![]() и
и![]() - независимые.
- независимые.
Для
пары
![]() и
и![]()
![]()
![]()
![]()
![]()
![]()
![]()
справедливо
(2.5). События
![]() и
и![]() зависимы.
зависимы.
Для
пары
![]() и
и![]() ,
без проверки условий (2.4), (2.5) можно
сказать, что события зависимы, т.к. они
несовместны. Для несовместных событий
(по определению) появление одного
исключает появление другого, т.е. обращает
в нуль его вероятность.
,
без проверки условий (2.4), (2.5) можно
сказать, что события зависимы, т.к. они
несовместны. Для несовместных событий
(по определению) появление одного
исключает появление другого, т.е. обращает
в нуль его вероятность.
Несколько
событий
![]() называютсяпопарно
независимыми, если
каждые два из них независимы.
называютсяпопарно
независимыми, если
каждые два из них независимы.
Несколько
событий
![]() называютсянезависимыми
в совокупности, если
каждые 2 из них независимы и независимы
каждое событие и все возможные произведения
остальных.
называютсянезависимыми
в совокупности, если
каждые 2 из них независимы и независимы
каждое событие и все возможные произведения
остальных.
Следствие из теоремы умножения 1
Для
независимых событий
![]() и
и![]() (2.1) имеет вид
(2.1) имеет вид
![]() (2.6)
(2.6)
Пример:
В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара (события
 и
и ).
Найти вероятность того, что оба шара
белые
).
Найти вероятность того, что оба шара
белые .
.
Решение.
![]() .
По (2.1)
.
По (2.1)
![]()
Те же условия, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются.
Решение.
По (2.6)
![]()
Теорема умножения 2
Вероятность
произведения нескольких событий
![]() ,
,![]() ,
…,
,
…,![]() равна произведению вероятности одного
из них на условные вероятности всех
остальных, причем вероятность каждого
последующего события вычисляется в
предположении, что все предыдущие уже
появились
равна произведению вероятности одного
из них на условные вероятности всех
остальных, причем вероятность каждого
последующего события вычисляется в
предположении, что все предыдущие уже
появились
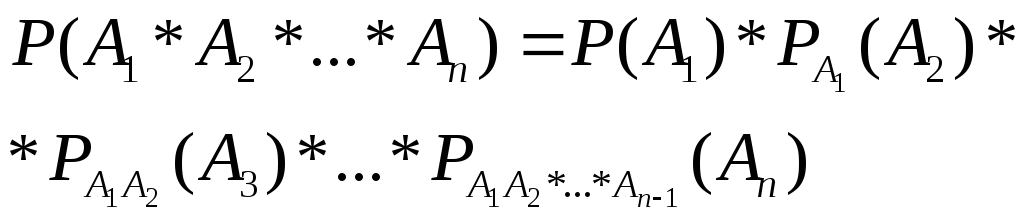 (2.7)
(2.7)
Следствие из теоремы умножения 2.
Вероятность
произведения нескольких событий
![]() ,
,![]() ,
…,
,
…,![]() ,
независимых в совокупности, равна
произведению вероятностей этих событий
,
независимых в совокупности, равна
произведению вероятностей этих событий
![]() (2.8)
(2.8)
Пример:
В урне 5 белых, 4 черных и 3 синих шара. Из урны вынимают подряд 3 шара. Найти вероятность того, что все 3 шара будут разноцветными.
Решение.
![]() -
вытащить первым белый шар;
-
вытащить первым белый шар;
![]() -
вытащить вторым черный шар;
-
вытащить вторым черный шар;
![]() -
вытащить третьим синий шар.
-
вытащить третьим синий шар.
По (2.7)
![]()
![]()
Те же условия, но после каждого
вынимания шар возвращается в урну, и шары в урне перемешиваются.
Решение.
По (2.8)
![]()
![]()
Теорема сложения вероятностей
Суммой двух событий
![]() и
и
![]() называется
событие
называется
событие
![]() ,
состоящее в появлении события
,
состоящее в появлении события![]() ,
события
,
события![]() ,
или обоих вместе. Для несовместных
событий
,
или обоих вместе. Для несовместных
событий![]() - появление либо
- появление либо![]() ,
либо
,
либо![]() ,
т.е. только одного из двух событий.
,
т.е. только одного из двух событий.
Суммой
нескольких событий
![]() называется
событие
называется
событие
![]() ,состоящее
в появлении хотя бы одного из
,состоящее
в появлении хотя бы одного из
![]() (для несовместных событий – только
одного).
(для несовместных событий – только
одного).
Пример:
1.
Если
![]() - попадание в цель при первом выстреле,
событие
- попадание в цель при первом выстреле,
событие![]() - попадание в цель при втором выстреле,
то событие
- попадание в цель при втором выстреле,
то событие![]() есть попадание в цель вообще, безразлично
при каком выстреле – при первом, при
втором или при обоих вместе.
есть попадание в цель вообще, безразлично
при каком выстреле – при первом, при
втором или при обоих вместе.
2. Если опыт состоит в пяти выстрелах
по мишени и рассматриваются события
![]() - ни одного попадания;
- ни одного попадания;
![]() - ровно одно попадание;
- ровно одно попадание;
![]() - ровно два попадания;
- ровно два попадания;
![]() - ровно три попадания;
- ровно три попадания;
![]() - ровно четыре попадания;
- ровно четыре попадания;
![]() - ровно пять попаданий;
- ровно пять попаданий;
то
![]()
![]() есть событие «не более двух попаданий»;
есть событие «не более двух попаданий»;
а
![]() - событие «не менее трех попаданий»
- событие «не менее трех попаданий»
Теорема сложения 1
Вероятность
суммы двух совместных событий
![]() и
и![]() равна сумме вероятностей этих событий
без вероятности их совместного появления.
равна сумме вероятностей этих событий
без вероятности их совместного появления.
![]() (2.10)
(2.10)
Если
![]() и
и![]() - зависимые события, то (2.10) принимает
вид
- зависимые события, то (2.10) принимает
вид
![]() (2.11)
(2.11)
Если
![]() и
и![]() - независимые события, то (2.10) имеет вид.
- независимые события, то (2.10) имеет вид.
![]() (2.12)
(2.12)
Вероятность
суммы двух несовместных событий
![]() и
и![]() равна сумме вероятностей
равна сумме вероятностей
этих событий
![]() (2.13)
(2.13)
Формулу
(2.13) можно рассматривать как частный
случай (2.10), т.к. для несовместных событий
![]() .
.
Пример. Вероятность попадания в цель при стрельбе первого и второго стрелка соответственно равны.
![]() ,
,![]() .
Найти вероятность попадания хотя бы
одним стрелком при одновременном
выстреле.
.
Найти вероятность попадания хотя бы
одним стрелком при одновременном
выстреле.
Решение.
![]() - попадание первого стрелка;
- попадание первого стрелка;
![]() - попадание второго стрелка.
- попадание второго стрелка.
По (2.12)
![]() ,
т.к.
,
т.к.
![]() и
и
![]() являются совместными и независимыми
являются совместными и независимыми
![]()
Теорема сложения 2
В
виду громоздкости общей формулы расчета
вероятности суммы совместных событий,
рассмотрим частный случай теоремы
сложения для трех событий
![]() ,
,![]() ,
,![]() (2.14)
(2.14)

Для
нескольких несовместных событий
![]() вероятность их суммы равна
вероятность их суммы равна
![]() (2.15)
(2.15)
Пример.
В
партии из
![]() изделий
изделий![]() изделий бракованных. Для контроля из
партии наугад берут
изделий бракованных. Для контроля из
партии наугад берут![]() изделий. Какова вероятность того, что
среди них будет не больше
изделий. Какова вероятность того, что
среди них будет не больше![]() бракованных (событие
бракованных (событие![]() )?
)?
Решение.
![]() -
среди взятых на проверку изделий ни
одного бракованного;
-
среди взятых на проверку изделий ни
одного бракованного;
![]() -
среди взятых на проверку изделий одно
бракованное;
-
среди взятых на проверку изделий одно
бракованное;
…
![]() -
среди взятых на проверку изделий
-
среди взятых на проверку изделий
![]() бракованных изделий.
бракованных изделий.
Тогда
![]() .
Т.к.
.
Т.к.![]() ,
,
![]() ,
…,
,
…,
![]() - несовместные события, то
- несовместные события, то
![]() по (2.15).
по (2.15).
Вероятность
события
![]() вычисляем по (1.7):
вычисляем по (1.7):
![]() ,
,
![]() ,
,![]()
Т.о.
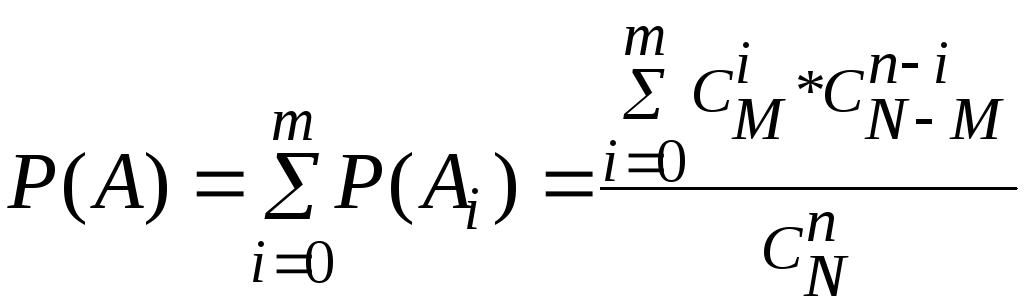
Следствие из теоремы сложения 2
Если
события
![]() образуют полную группу попарно
несовместных событий, то сумма их
вероятностей равна 1.
образуют полную группу попарно
несовместных событий, то сумма их
вероятностей равна 1.
![]() (2.16)
(2.16)
Пример
Для
АТС вероятность появления вызова с
квартирного телефона
![]() ,
с таксофона -
,
с таксофона -![]() .
Остальные вызовы дают учрежденческие
телефоны. Найти вероятность появления
учрежденческого вызова.
.
Остальные вызовы дают учрежденческие
телефоны. Найти вероятность появления
учрежденческого вызова.
![]()
![]()
Частный случай следствия из теоремы сложения 2
Сумма вероятностей противоположных событий равна 1
![]() (2.17)
(2.17)
Обычно
обозначают
![]() ,
,![]() ,
тогда (2.17) примет вид
,
тогда (2.17) примет вид![]()
Применение теорем умножения и сложения
На практике сравнительно редко встречаются задачи, в которых нужно применять только теорему умножения или только теорему сложения вероятностей. Обычно эти теоремы приходится применять совместно. При этом, как правило, событие, вероятность которого требуется определить, представляется в виде суммы и (или) произведений нескольких несовместных (совместных) событий.
Пример.
По
мишени стреляют 3 стрелка. Вероятность
попадания для них
![]() ,
,![]() ,
,![]() .
Найти вероятность следующих событий:
.
Найти вероятность следующих событий:
B – ни одного попадания;
C – только 1 попадание;
D – только 2 попадания;
E – только 3 попадания;
F – хотя бы одно попадание.
Решение.
![]()
![]() по
(2.8), т.к. события
по
(2.8), т.к. события
![]() - независимы в совокупности.
- независимы в совокупности.
![]() по
(2.17)
по
(2.17)
![]()
Аналогично
![]()
![]()
![]()
![]()
![]()
![]()
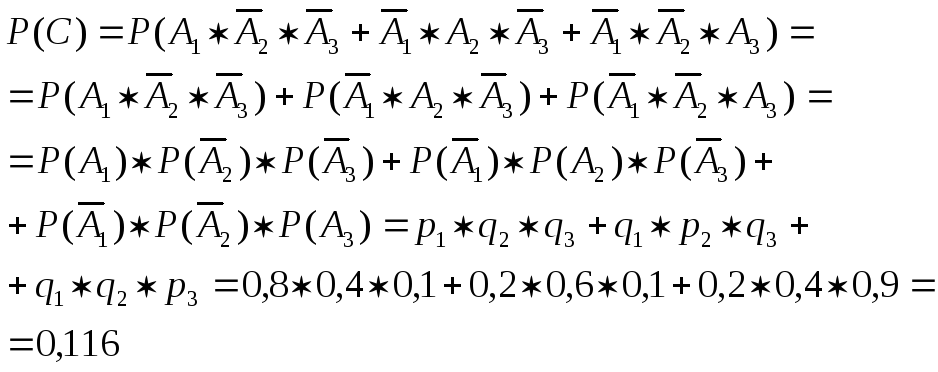
![]()
![]()
![]()
![]()
События В, С, D, Е образуют полную группу попарно несовместных событий. Проверим (2.16)
![]()
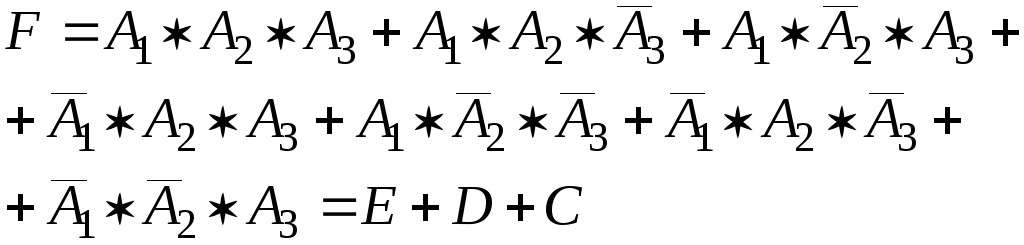
![]()
Однако такой путь решения задачи слишком сложен. Здесь проще от прямого события F перейти к противоположному событию – ни одного попадания – что соответствует событию B.
Поэтому
![]()
![]()
![]()
На
примере вычисления
![]() проиллюстрирован
принцип
целесообразности применения противоположных
событий в
теории вероятностей – если противоположное
событие распадается на меньшее число
вариантов, чем прямое событие, то имеет
смысл при вычислении вероятностей
переходить к противоположному событию.
проиллюстрирован
принцип
целесообразности применения противоположных
событий в
теории вероятностей – если противоположное
событие распадается на меньшее число
вариантов, чем прямое событие, то имеет
смысл при вычислении вероятностей
переходить к противоположному событию.
