
posobia_4semФизика / Квантовая оптика _решебник_
.pdf
N 0,45 0,55 10 6 3 3,736 1018 . 6,626 10 34 3 108
2) Сила светового давления на поверхность равна:
F=р·S.
Световое давление может быть найдено по формуле:
р Ee (1 , c
(1)
(2)
где Eе – энергетическая освещённость, ρ – коэффициент отражения, с – скорость света. Подставляя (2) в (1), получим:
F |
S Eе |
(1 ), |
(3) |
|
|||
|
c |
|
|
Т.к. произведение S Eе Фе - поток (мощность) энергии излучения, то
(3) можно записать в виде:
F Фcе (1 ),
Подставим численные значения:
F |
0,45 |
(1 1) 0,3 10 8 |
3(нН). |
|
3 108 |
||||
|
|
|
Ответ: N = 3,736·1018; F = 3 нН.
Домашнее задание № 4
Определить поверхностную плотность потока энергии излучения, падающего на зеркальную поверхность, если световое давление р при перпендикулярном падении лучей равно 10 мкПа.
Дано: |
СИ: |
Решение: |
р = 10 мкПа |
10-5Па |
Поверхностная плотность потока энергии из- |
ρ = 1 |
|
лучения равна плотности потока энергии излучения, |
с = 3·108 м/с |
|
падающего на поверхность Ее (облучённость поверхно- |
φ = ? |
|
сти): |
φ = Ее.
Давление света при нормальном падении на поверхность можно найти по формуле:
р Ece (1 ) ,
где Ee – так же энергетическая освещённость (мощность излучения падающе-
го на единицу поверхности), - коэффициент отражения, с – скорость света. Тогда:
61

Ee c р .
Вычислим и получим:
|
3 108 |
10 5 |
1,5 |
10 |
3 Вт |
1,5 |
кВт |
. |
|
1 1 |
м2 |
м2 |
|||||||
|
|
|
|
|
|||||
Ответ: φ = 1,5 кВт/м2.
Домашнее задание № 5
Найти давление света на внутреннюю п о- верхность колбы стоваттной электрической лампы.
Колба лампы представляет собой сферический с о- R суд радиусом 5см (рис. 1). Внутренняя поверхность колбы отражает 10% падающего на нее света. Сч и- тать, что вся потребляемая лампой энергия идет на излучение.
Дано: |
|
|
СИ: |
|
|
|
|
Решение: |
|
Рис. 1 |
||
|
|
|
|
|
|
|||||||
Фе = 100 Вт |
|
|
|
|
|
Давление света |
при |
|
||||
R = 5 см |
|
|
0,05 м |
|
нормальном давлении на поверхность: |
|||||||
ρ = 0,1 |
|
|
|
|
|
|
|
|
р |
Ee |
(1 ) , |
(1) |
с = 3·108 м/с |
|
|
|
|
|
|
c |
|||||
|
|
|
|
|
|
где Eе – энергетическая освещённость (энергия, падаю- |
||||||
р = ? |
|
|
|
|
|
|||||||
щая на единицу поверхности в единицу времени ), ρ – коэффициент отражения, c |
||||||||||||
– скорость света в вакууме. |
|
|
|
|
|
|
||||||
Мощность излучения: |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Фе = Eе·S, |
|
(2) |
|
где S – площадь внутренней поверхности колбы. |
|
|||||||||||
Из (2) выразим энергетическую освещённость Eе подставим её в (1) с учё- |
||||||||||||
том того, что Sсферы = 4πR2, получим давление: |
|
|
||||||||||
р |
Фe |
1 |
Фe |
|
1 . |
|
|
|||||
|
Sc |
4 R2c |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
Подставим численные значения: |
|
|
||||||||||
р |
|
|
100 |
|
|
1 0,1 0,1167 10 4 11,7 |
( мкПа). |
|||||
|
4 |
3,14 52 10 4 3 |
108 |
|||||||||
|
|
|
|
|
|
|||||||
Ответ: р = 11,7 мкПа.
62

Домашнее задание № 6
Спутник в форме шара движется вокруг Земли на такой высоте, что п о- глощением солнечного света в атмосфере можно пренебречь. Диаметр спутника d = 40 м. Зная солнечную постоянную (см. задачу №13) и принимая, что п о- верхность спутника полностью отражает свет, определить силу давления F солнечного света на спутник.
Дано: |
СИ: |
|||
С = 1,4 |
кДж |
1,4∙103 |
Дж |
|
м2 с |
м2 с |
|||
|
|
|||
ρ = 1
d = 40 м
с = 3·108 м/с F = ?
нормальном падении:
Решение:
Сила светового давления на поверхность равна произведению светового давления p на площадь S поверхности:
F = р·S,
где S = |
d 2 |
– площадь сечения спутника. |
|
4 |
|
Давление, производимое светом при
р Ece 1 ,
где, ρ – коэффициент отражения, с – скорость света в вакууме, Ее – плотность потока энергии излучения, падающего на поверхность (энергетическая осв е- щённость или облучённость поверхности). Что совпадает с Солнечной постоянной С (см. задачу №13), т.е.
Ее = С.
Тогда давление:
р Сc 1 .
Подставляя выражение давления света р и площади окружности S в формулу силы светового давления F, получим:
F |
С |
1 |
|
d 2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|||
|
c |
|
|
|
|
|
|
||
Произведём вычисления в системе СИ: |
|
||||||||
F 1,4 103 |
1 1 |
3,14 402 |
|
14067,2 |
10 5 |
= 1172·10-5 =11,72·10-3 Н ≈ |
|||
3 108 |
|
4 |
|
12 |
|
|
|||
11,7 мН.
Ответ: F = 11,7 мН.
63

Практическое занятие 4 ЭФФЕКТ КОМПТОНА
Рекомендуемое задание № 1
Рентгеновское излучение длиной волны 55,8 пм рассеивается плиткой графита (Комптон-эффект). Определить длину волны света, рассеянного под углом 60 к направлению падающего пучка света.
Дано: |
|
Си: |
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
55,8 пм |
|
55,8 10-12м |
|
Формула для эффекта Комптона: |
|
|
|
|
||
60° |
|
|
|
С (1 |
cos ) 2 С sin |
2 |
|
|
, |
|
|
|
|
|
|
|
|
|
|||
=? |
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
||
где – длина волны рассеянного (отразившегося) фотона на частице (эле к- трон, протон, нейтрон…), λ – длина волны падающего фотона, λ – разность
этих длин волн, |
С |
h |
2,426пм – комптоновская длина волны для элек- |
|
m0c |
||||
|
|
|
трона, m0 – масса покоя электрона отдачи.
Отсюда длина волны рассеянного (отразившегося) света:
С (1 cos ). Подставим численные значения:
55,8 10 12 2,426 1 0,5 55,8 10 12 1,213 10 12 57 (пм).
Ответ: = 57 пм.
Рекомендуемое задание № 2
Определить максимальное изменение длины волны при комптоновском рассеянии: 1) на свободных электронах; 2) на свободных протонах.
Дано: |
|
Решение: |
||
|
||||
1) mе = 9,11·10-31 кг |
|
Формула для эффекта Комптона: |
||
2) mр = 1,67·10-27 кг |
|
С (1 cos ) |
h |
|
h =6,63·10-34 Дж·с |
|
|
(1 cos ) , |
|
m c |
||||
с = 3·108 м/с |
|
0 |
|
|
|
Проанализируем формулу. Максимальное из- |
|||
λmax = ? |
|
менение длины волны λ при комптоновском рассея- |
||
нии наступит при условии сosθ = –1 (θ = 180 ) т.е. (1 – сosθ) = 2. Тогда:
max 2 mhc .
0
Выполним промежуточные вычисления:
64
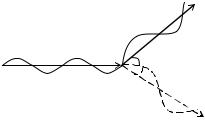
С |
|
h |
|
|
|
|
6,63 10 34 |
2,426 10 12 м 2,426пм |
- |
комптоновская |
||||
mе c |
|
9,11 10 31 3 |
108 |
|||||||||||
|
|
|
|
|
|
|
|
|||||||
длина волны для электрона; |
|
|
|
|
|
|||||||||
С , р |
h |
|
|
|
6,63 10 |
34 |
|
1,32 10 15 м 1,32фм |
- |
комптоновская |
||||
mр c |
1,67 10 27 |
3 108 |
||||||||||||
|
|
|
|
|
|
|
||||||||
длина волны для протона; |
|
|
|
|
|
|||||||||
|
|
|
||||||||||||
Вычислим максимальное изменение длины волны |
λ |
при комптонов- |
||||||||||||
ском рассеянии: |
|
|
|
|
|
|
|
|
|
|
||||
max,е |
2 2,426пм 4,852пм для электрона (пикометров); |
|||||||||||||
max, р |
2 1,32фм 2,64фм для протона (фемтометров). |
|
||||||||||||
Ответ: 1) |
|
|
|
λmax,е = 4,852 пм; 2) λmax,р = 2,64 фм. |
|
|
||||||||
Рекомендуемое задание № 3
Определить угол рассеяния фотона, испытавшего соударение со св о- бодным электроном (рис. 1), если изменение длины волны при рассеянии равно 3,62 пм.
Дано: |
|
Си: |
|
|
Решение: |
|
||||
|
|
|
|
|||||||
∆λ = 3,62 пм |
3,62 10-12 м |
|
|
Изменение длины волны фотона в р е- |
||||||
λС = 2,426 пм |
2,426 10-12 м |
зультате рассеяния на |
свободном эле ктроне |
|||||||
|
|
|
|
|
|
(эффект Комптона): |
|
|||
θ = ? |
|
|
|
|
|
|
||||
С (1 cos ), |
|
|
|
|
|
|
|
λ/ |
||
где λС – комптоновская длина волны для |
|
|||||||||
электрона. Выразим угол рассеяния: |
|
|
λ |
|||||||
|
|
|
|
|
|
|
|
|
- |
|
arccos 1 |
. |
|
|
|
|
|
|
|||
|
|
C |
|
|
|
|
|
|
Рис. 1 |
|
Подставим значения: |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
3,62 |
|
|
|
3,62 |
|
|
||
arccos 1 |
|
|
|
arccos 1 |
|
|
120 . |
|
||
|
|
2,426 |
|
|||||||
|
|
2,426 |
|
|
|
|
|
|||
Ответ: θ = 120 или 240 (на рисунке пунктиром).
Рекомендуемое задание № 4
Фотон с энергией 0,4 МэВ рассеялся под углом 90 на свободном электроне (рис. 2). Определить энергию рассеянного фотона и кинетическую энергию T электрона отдачи.
65

Дано: |
|
|
|
Си: |
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
ε = 0,4 МэВ |
|
|
0,64·10-14 Дж |
|
|
|
1. Энергию рассеянного фотона |
най- |
|||||||||||||||||||||||||||||||
θ = 90° |
|
|
|
8,16·10-14 Дж |
|
дем, воспользовавшись формулой Комптона: |
|||||||||||||||||||||||||||||||||
Е0 = 0,511 МэВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
1 cos . |
|
|
||||||||||||||||||||
? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m ·c |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
T ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выразив длины волн рассеянного и |
||||||||||||||||||||
падающего |
|
фотонов |
|
через энергии |
|
|
|
|
hc |
и |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
hc соответствующих фотонов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε / |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|||||
|
hc |
hc |
|
|
h |
|
|
1 cos . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
m·c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2 |
|
Т |
||||||||
Разделим обе части этого равенства на hc: |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
1 |
|
|
|
1 1 cos |
|
1 cos . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
mc2 |
|
|
Е0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Отсюда, обозначив для краткости энергию покоя электрона Е0 |
= mc2 = |
||||||||||||||||||||||||||||||||||||||
9,11·10-31·9·1016 = 8,16·10-14 Дж, найдем энергию рассеянного фотона: |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 cos Е0 |
|
|
|
|
|
|
|
1 cos 1 |
|
|
|||||||||||||
|
1 |
|
|
|
1 cos |
|
|
1 |
|
|
|
|
Е0 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||||||||||||||
|
|
|
Е0 |
|
|
|
|
|
|
|
Е0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Следовательно, энергия рассеянного фотона: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 cos Е |
|
|
|
|
|
|
|
|
|
|
сos 1 |
. |
|
|
(1) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Подставив числовые значения величин, получим : |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
0,4 |
|
|
0,224МэВ 224кэВ = 0,36 10 |
-13 |
Дж. |
|||||||||||||||||||||
|
0,4 |
|
|
|
|
|
|
|
|
|
|
1,783 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
0,511 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. Кинетическая энергия электрона отдачи Т, как это следует из за- |
|||||||||||||||||||||||||||||||||||||||
кона сохранения энергии: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
= |
+ Т, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
равна разности между энергией падающего фотона и энергией рассеянного фотона:
T = 0,4 – 0,224 = 0,176 МэВ = 176 кэВ.
T = 0,64·10-13 – 0,36·10-13 = 0,28·10-13 Дж.
Ответ: = 224 кэВ = 0,36 10-13 Дж, Т = 176 кэВ = 0,28·10-13 Дж.
Примечание 1: 1 МэВ = 1,6·10-13 Дж.
66
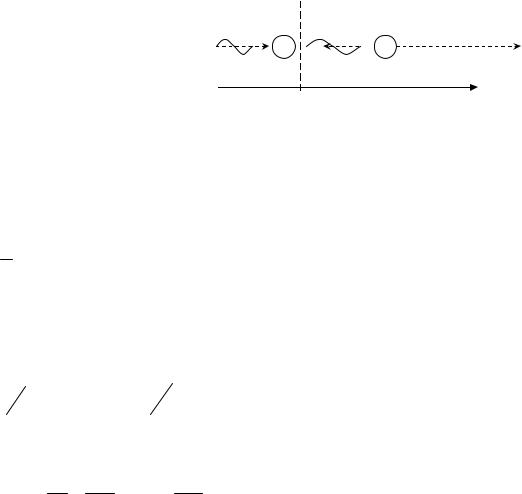
Примечание 2: Вывод формулы кинетической энергии электрона отд ачи:
|
|
|
|
|
|
|
|
|
Е |
|
|
2 |
1 cos Е |
|
Е |
|
|
|
2 |
|
cos |
|
|
|
|||||||
T |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
1 |
|
|
|
||||||||
1 cos Е0 |
|
|
|
1 cos Е0 |
|
|
1 cos Е0 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Рекомендуемое задание № 5 |
|
|
|
|
|
|
|
|
|
|||||||||||
Определить импульс pe |
электрона отдачи при эффекте Комптона, если |
||||||||||||||||||||||||||||||
фотон с энергией, равной энергии |
покоя электрона, был |
рассеян |
на угол |
||||||||||||||||||||||||||||
180 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Дано: |
|
|
|
|
|
|
СИ: |
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
180 |
|
|
|
|
8,16·10-14 Дж |
|
|
По закону сохранения импульса: |
|||||||||||||||||||||||
Е0 = 0,511МэВ |
|
|
р р ре , |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
λС =2,426 пм |
|
|
|
|
2,426·10-12 м |
|
|
где |
р – импульс падающего света, |
р – им- |
|||||||||||||||||||||
ре -? |
|
|
|
|
|
|
|
|
|
|
|
пульс рассеянного |
|
(отразившегося |
ф отона) |
||||||||||||||||
света, ре – импульс электрона. В проекции на ось ОХ (рис. 3): |
|
|
|
|
|
||||||||||||||||||||||||||
р = – р' + ре. |
|
|
|
|
|
|
р |
|
|
|
|
|
р |
|
ре |
|
|
||||||||||||||
Откуда импульс электрона: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
ре = р + р'. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mе |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
до mе |
|
|
|
|
|
|
|
|
|
Х |
|||||||||||
Распишем импульсы фотона: |
|
|
|
после |
|
|
|
|
|||||||||||||||||||||||
|
h |
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
р и |
|
р |
. |
|
|
|
|
|
|
|
|
|
|
|
Рис. 3 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Тогда импульс электрона: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
pe |
h |
|
|
h |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 способ. Через энергию. Умножим на «с», чтобы получить энергию ф о- тона h c . Тогда импульс электрона:
pe c hc |
hc |
|
|
|
|
|
|
|
|
|
(1). |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Энергия рассеянного фотона (вывод см. задача № 4): |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Е0 |
|
|
Е0 |
|
Е0 |
|
|
|
|
|
|
|
|
|
Е |
0 |
|
1 1 1 |
3 . |
||||||
|
|
|
||||||||||||||||
|
|
|
|
Е0 |
1 сos 1 |
|
|
1 сos180 1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Е0 |
|
|
|
|
|
||
Подставили ε = Е0 и θ = 180º. Подставим в формулу (1), и выразим и м- пульс фотона:
pec Е0 Е30 43Е0 pe 43Еc0 . Подставим числа:
67

pe |
4 8,16 10 14 |
|
32,64 |
10 22 |
3,63 10 22 |
кг·м/c. |
|
3 3 108 |
9 |
||||||
|
|
|
|
|
2способ. Через λС. Применим формулу для эффекта Комптона:
С 1 cos ,
где – длина волны рассеянного (отразившегося) фотона на электроне, |
λ – |
|||
длина волны падающего фотона, λ – разность этих длин волн, С |
h |
|
– |
|
m0c |
||||
|
|
|||
комптоновская длина волны для электрона, m0 – масса покоя электрона отдачи. Выразим – длину волны рассеянного фотона:
С 1 cos . Т.е. импульс электрона:
pe |
h |
|
h |
|
. |
|
|
С 1 cos |
|||||
|
|
|
||||
Длину волны фотона выразим через энергию фотона:
h c => h c .
С учетом этой формулы импульс электрона:
pe |
h |
|
|
|
|
h |
|
|
|
|
|
|
|
h |
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
h |
c |
|
|
h |
c |
|
c (1 cos ) |
c |
h |
c (1 cos1800 ) |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подставим числа: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
p |
|
|
8,16 10 14 |
|
|
|
|
|
6,63 10 34 |
|
|
|
, |
|
|
|
|
|
|||||||||||
e |
|
|
3 108 |
6,63 10 34 |
3 108 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2,426 10 12 (1 1 ) |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
8,16 10 14 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
pe |
2,72 10 22 |
|
|
6,63 10 34 |
|
|
|
2,72 10 22 |
|
6,63 10 |
34 |
, |
|||||||||||||||||
2,4375 |
10 12 |
4,852 |
10 12 |
7,2895 |
10 |
12 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
pe |
2,72 10 22 |
0,91 10 22 |
3,63 10 22 кг·м/c. |
|
|
|
|
|
|
|
|||||||||||||||||||
Ответ: ре = 3,63·10 -22 кг·м/c. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Примечание 1: 1 МэВ = 1,6·10-13 Дж. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Рекомендуемое задание № 6
Какая доля энергии фотона при эффекте Комптон а приходится на электрон отдачи, если фотон претерпел рассеяние на угол 180 ? Энергия фотона до рассеяния равна 0,255 МэВ.
68

Дано: |
|
Решение: |
|
||
180 |
|
Закон сохранения энергии: |
0,255 МэВ |
|
= + Т, |
Е0 = 0,511 МэВ |
|
где – энергия падающего фотона, ε/ – энергия рассеянно- |
T ? |
|
го (отразившегося) фотона, Т – кинетическая энергия |
|
|
электрона. |
Выразим |
|
кинетическую энергию электрона отдачи Т: |
T .
Тогда отношение кинетической энергии электрона отдачи к энергии падающего фотона:
|
|
|
|
|
|
|
|
|
|
T |
|
1 |
. |
(1) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Энергия рассеянного фотона (вывод см. задача № 4): |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
сos 1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Е0 |
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Откуда: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
сos 1 |
|
|
|
||||||||
|
|
|
|
|
Е0 |
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставим в формулу (1): |
|
|
|
||||||||||||||
T |
|
1 |
|
|
|
|
1 |
|
|
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
1 сos |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Е0 |
|
|
|
|
|
|
|
|
Произведём вычисления вне системы СИ: |
|||||||||||||||||
T |
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
1 |
1 . |
|||
|
|
|
0,255 |
|
1 1 |
||||||||||||
|
|
|
|
|
|
2 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
0,511 |
|
|
|
|
|
|
|||
Ответ: T 0,5 .
Примечание: 1 МэВ = 1,6·10-13 Дж.
Рекомендуемое задание № 7
Фотон с энергией 0,25 МэВ рассеялся на свободном электроне. Энергия рассеянного фотона равна 0,2 МэВ. Определить угол рассеяния .
69
Дано: |
|
Си: |
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0,25 МэВ |
|
0,4 10-13 Дж |
|
Воспользуемся формулой |
Комптона в |
|||||
= 0,2 МэВ |
|
0,32 10-13 Дж |
|
виде: |
|
|
|
|
|
|
Е0 = 0,511 МэВ |
|
|
|
2 |
h |
sin |
2 |
|
, |
(1) |
? |
|
|
|
m 0 c |
|
2 |
||||
|
|
|
|
|
|
|
|
|||
где – длина волны рассеянного (отразившегося) фотона на электроне, λ – длина волны падающего фотона, m0 – масса покоя электрона отдачи, h – постоянная планка, с – скорость света в вакууме.
Выразим длины волн и через соответствующие энергии и фотонов, воспользовавшись соотношением:
hc и hc => hc и hc ; Подставим в формулу (1) и сократим на hc:
hс |
|
hc |
2 |
h |
sin |
2 |
=> |
1 |
|
|
1 |
2 |
1 |
|
sin |
2 |
или |
|
2 |
1 |
sin |
2 |
|
. |
||
|
|
|
m0c |
2 |
|
|
|
|
m0c |
2 |
2 |
|
Е0 |
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Учли, что энергия покоя электрона Е0 = m0c2. Выразим искомый угол:
sin2 |
E0 ( ) |
=> sin |
|
|
|
|
. |
|||
|
E0 ( ) |
=> 2 arcsin |
E0 ( ) |
|||||||
|
|
|
2 |
|||||||
2 |
|
2 |
2 |
|
|
|
2 |
|||
Подставим числа вне системы СИ: |
|
|
|
|||||||
|
|
|
|
|
||||||
2arcsin |
|
0,511(0,25 0,2) |
2arcsin0,50547 2 30,3626 |
|||||||
|
|
|
2 0,25 0,2 |
|
|
|
|
|
||
60,725 60 43,5 .
Ответ: θ = 60 43,5' или 299 16,5'.
Примечание: 1 МэВ = 1,6·10-13 Дж.
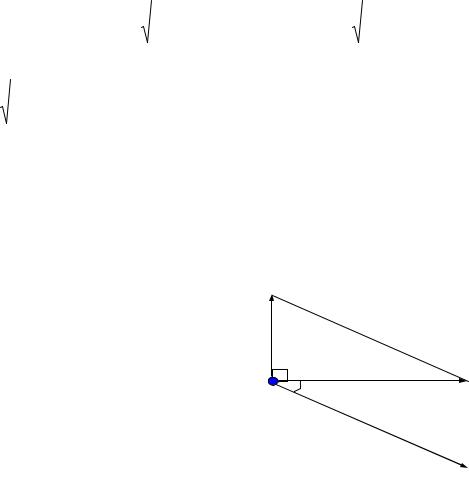
Рекомендуемое задание № 8
Угол рассеяния фотона равен 90 (рис. 4). Угол отдачи электрона ра-
вен 30 . Определите энергию |
падающего |
p |
|
|
||||
фотона. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
Дано: |
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
90 |
|
Закон сохранения им- |
|
|
p |
|||
30 |
|
пульса, |
согласно |
которому |
|
|
||
|
|
|||||||
Е0 = 0,511 МэВ |
|
импульс |
падающего |
фотона |
|
|
||
|
|
|
|
|||||
|
|
р равен |
векторной |
сумме |
|
|
|
|
? |
|
|
|
|
||||
импульсов рассеянного фотона р |
и электро- |
|
|
|
||||
на отдачи ре m : |
|
|
|
Рис. 4 |
m |
|||
70
