2.5. Властивості випадкових похибок

Розглядаючи|розглядувати| властивості випадкових похибок, матимемо на увазі не їх індивідуальні властивості, а найбільш загальні|спільні| інтегральні властивості, які мають достатньо|досить| великі сукупності цих похибок.

У теорії похибок виділяють чотири такі властивості.

Властивість обмеженості. За певних умов вимірів випадкова похибка за абсолютною величиною не може перевищити певну відому межу. Ця межа називається граничною похибкою. Позначивши її Δ_гр, цю властивість можна виразити нерівністю

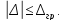(2.10)

Властивість компенсації. Якщо ряд вимірів однієї або декількох величин здійснюється в одних і тих же умовах, то сума випадкових похибок, що ділиться на їх кількість, при необмеженому збільшенні ряду вимірів в границі наближається до нуля, тобто

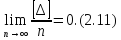
У виразі (2.11) і надалі використовуватимемо символіку К.Ф. Гаусса, де квадратні дужки означають суму однорідних величин. Наприклад,

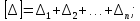
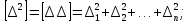
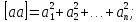(2.12)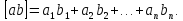

Властивість незалежності. Якщо здійснюється два ряди вимірів з випадковими похибками: 1) Δ'₁, Δ'₂,…, Δ'_n і 2) Δ''₁, Δ''₂,…, Δ''_n, то сума попарних добутків цих похибок, що ділиться на кількість цих добутків, при необмеженому зростанні кількості вимірів в границі наближається до нуля.

Використовуючи символіку К.Ф.Гаусса, цю властивість можна записати формулою

Ця властивість не є|з'являється| всеохоплюючою|усеосяжною|. У геодезичній практиці зустрічаються не часто, але|та| зустрічаються залежні випадкові похибки.

Властивість розсіювання. Якщо ряд вимірів здійснюється за одних і тих же умов, то для випадкових похибок має місце межа

Величина σ називається стандартом. Квадрат стандарту σ² називають дисперсією, а величину

де с – довільне позитивне число називають вагою.

Із|із| співвідношень (2.14) і (2.15) виходить: ряди|лави| вимірів|вимірів|, виконані з|із| більшою точністю, мають менший стандарт та дисперсію і більшу вагу.

Додаткові джерела інформації

1. Википедия [электронный ресурс] / Метрология #. Режим доступа. - http://ru. wikipedia. org/ wiki/ Заголовок с экрана 11.12.09.

2. Галилей [электронный ресурс] / Г. Галилей. - Режим доступа. - http://ru.

wikipedia.org/wiki/ Заголовок с экрана 01.08.09.

3. Рене Декарт. Рассуждение о методе, чтобы верно направлять свой разум и отыскивать истину в науках [электронный ресурс] / Рене Декарт.- Режим доступа. - http://psylib.org.ua/books/dekar01/ Заголовок с экрана 21.09.09.

4. Математика [электронный ресурс] / Сайт Комітету питань науки і освіти. - Режим доступу. - http://ru.wikipedia.org/wiki/ Заголовок с экрана 29.09.09.

5. Гюйгенс, Христиан. Энциклопедия «Кругосвет» [электронный ресурс] / Гюйгенс, Христиан. - Режим доступа. - http://slovari.yandex.ru/dict/

krugosvet/article/3/35/1003945.htm. Заголовок с экрана 17.08.09.

6. Паскаль, Блез [электронный ресурс] / Блез Паскаль. - Режим доступа. - http://ru.wikipedia.org/wiki/ Заголовок с экрана 17.08.09.

7. Ньютон, Исаак [электронный ресурс] / Исаак Ньютон. - Режим доступа. - http://ru.wikipedia.org/wiki/ Заголовок с экрана 09.07.09.

8. Колмогоров, А. Н. Математика XIX века [Текст] / А. Н. Колмогоров, А. П. Юшкевич. - М.: Наука, 1980. – 128 с.

9. Гаусс. Словари и энциклопедии [электронный ресурс] / К.Ф. Гаусс. - Режим доступа. - http://dic.academic.ru/dic.nsf/bse / Заголовок с экрана 19.09.09.

10. Гаусс, Карл Фридрих. Википедия [электронный ресурс] / К.Ф. Гаусс. - Режим доступа. - http://ru.wikipedia.org/wiki / Заголовок с экрана -6.06.09.

11. Войславский, Л.К. Теория математической обработки геодезических измерений. Часть 1. Теория погрешностей измерений [Текст] учебно-методическое пособие (для студентов 2 курса дневной формы обучения спец. 7.070908 «Геоинформационные системы и технологии») / Л.К. Войславский. – Х.: ХНАГХ, 2006. – 64 с.

12. Погрешность измерения [электронный ресурс] / Сайт Комітету питань науки і освіти. - Режим доступу. - http://ru.wikipedia.org/wiki/ Заголовок с экрана - 5.11.09.

13. Кемниц, Ю.В. Теория ошибок измерений [Текст]/ Ю.В.Кемниц. – М.: Недра, 1962. – 175 с.