Додаткові джерела інформації

1. Бурмистров, Г.А. Теория математической обработки геодезических измерений [Текст]: пособие / Г.А. Бурмистров, В.Д. Большаков. – М.: Недра, 1969. – 400 с.

2. Войславский, Л.К. Теория математической обработки геодезических измерений. Часть 1. Теория погрешностей измерений [Текст] учебно-методическое пособие (для студентов 2 курса дневной формы обучения спец. 7.070908 «Геоинформационные системы и технологии») / Л.К. Войславский. – Х.: ХНАГХ, 2006. – 64 с.

3. Зазуляк, П.М. Основи математичного опрацювання геодезичних вимірів [Текст] навчальний посібник / П.М. Зазуляк, В.І. Гавриш, Е.М. Євсєєва, М.Д. Йосипчук. – Львів: Видавництво «Растр-7», 2007. – 408 с.

5. Математична обробка ряду рівноточних результатів вимірів однієї і тієї ж величини

5.1. Проста арифметична середина і її властивості

Якщо – ряд|лава| незалежних результатів рівноточних| вимірів|вимірів| однієї і тієї ж величини Х, то за якнайкраще|щонайкраще| наближення до її дійсного значення зазвичай|звично| приймають просту арифметичну середину, яка обчислюється за елементарною формулою

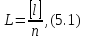
де n – кількість рівноточних| вимірів|вимірів|, а квадратні дужки означають суму результатів вимірів|вимірів| у символах К.Ф. Гаусса.

Такі обчислення|підрахунки| є|з'являються| правомірними, тому що вони враховують властивості арифметичної середини, які розглянемо|розглядуватимемо| нижче.

Властивості простої арифметичної середини

Властивість 1. Якщо результати вимірів вільні від систематичних похибок, то проста арифметична середина цих результатів при збільшенні кількості вимірів в межі наближається до дійсного значення вимірюваної величини, тобто

Враховуючи властивості систематичних похибок можна записати

Використовуючи результати доведення основної теореми теорії похибок, підсумуємо праві і ліві частини|частки| отриманих|одержувати| виразів і розділимо їх на n (див. доведення теореми в п.п. 4.1). Отримаємо

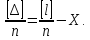
|одержуватимемо|Використовуючи вираз|вираження| (5.1), очевидно, що отриману|одержувати| рівність можна записати у вигляді|виді|

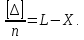
За n→∞ ліва частина цього виразу на підставі властивості компенсації випадкових похибок (2.11) наближається до нуля. Права його частина так само наближається до нуля, що доводить справедливість виразу (5.2).

Отже, проста арифметична середина L є|з'являється| спроможним оцінити величину Х.

Властивість 2. Арифметична середина незалежних рівноточних результатів вимірів має стандарт в раз менший стандарту σ цих вимірів.

Представимо|уявлятимемо| вираз|вираження| (5.1) у вигляді

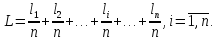
|виді|Скориставшись процедурами доведення основної теореми теорії похибок в отриманому виразі, візьмемо частинні похідні за кожною змінною l_i

тоді формула (4.2) набуває вигляду:

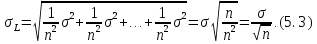
Наочно арифметичну середину рівноточних результатів вимірів можна представити, зобразивши графічно (рис. 5.1) ділянки розсіювання похибок Δ і Δ_L.

Рис. 5.1 – Ілюстрація розподілу похибок відносно арифметичної

середини рівноточних| вимірів|вимірів|

Ділянка можливого розсіювання похибок Δ_L буде тим вужча, чим більша кількість вимірів n. У зв'язку з цим виникає питання, чи є збільшення кількості вимірів ефективною процедурою підвищення їх точності? При n ≤ 10 на це питання можна відповісти позитивно. Але за збільшення кількості вимірів n точність вимірів змінюватиметься повільніше, ніж збільшення n. Так, для підвищення точності в 4 рази буде потрібно 16 вимірів, в 5 разів – 25, в 6 разів – 36, у 10 разів – 100 вимірів.

Крім того, завжди залишаються малі похибки порівняно з випадковими систематичними похибками, які не вдалося цілком виключити. Досягши деякого n вони стають переважаючими|пануючими| у величині L і перешкоджатимуть подальшому|дальшому| підвищенню точності. Таким чином, збільшення кількості вимірів,|вимірів| з одного боку, збільшує їх точність|вимірів|, з іншого боку, велика кількість вимірів|вимірів| вимагає великих витрат часу|затрат|, що може призвести до зміни умов і неминучого порушення рівноточних| вимірів|вимірів|.

Властивість 3. Якщо арифметична середина, отримана з результатів вимірів вільних від систематичних похибок, то і сама вона не містить систематичної похибки.

Припустимо зворотне, тобто результати вимірів містять систематичні похибки θ₁, θ₂,…, θ_i,…, θ_n. Тоді на підставі (2.9) можна записати:

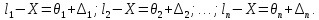
Склавши праві і ліві частини|частки| отриманих|одержувати| рівнянь між собою і розділивши їх на n, отримаємо

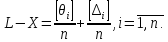
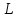|одержуватимемо|Права частина отриманого рівняння складається з двох доданків, що є систематичною і випадковою похибками арифметичної середини. Звідси випливає, що якщо θ₁= θ₂=…= θ_n=0, то і дорівнюватиме 0, що і доводить сформульовану вище властивість.

Таким чином, за відсутності систематичних похибок арифметична середина L є не тільки спроможним, але і незміщеним оцінюванням величини Х. Таку оцінку в геодезії називають найймовірнішим значенням вимірюваної величини.

За наявності систематичних похибок арифметична середина також міститиме|утримуватиме| систематичну похибку

а тому не має властивостей 1 і 3. У цьому випадку арифметична середина L хоча і дасть якнайкраще|щонайкраще| з|із| можливих наближень до Х, але|та| не буде її найймовірнішим| значенням.

Раніше було відзначено, що вплив випадкових похибок можна ослабити належною математичною обробкою. Такого роду обробку називають зрівнюванням результатів вимірів.

Результати вимірів зрівнюють шляхом введення в обчислення поправок. Під точною поправкою 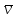розумітимемо величину, додавши яку до результатів вимірювання l отримаємо значення Х, тобто

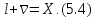
Перетворимо отриманий|одержувати| вираз|вираження| і представимо його у вигляді|виді|:

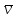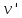З отриманого співвідношення випливає, що точна поправка за абсолютною величиною дорівнює похибці, але протилежна їй за знаком. Відзначимо, що знайти точні поправки у більшості випадків геодезичної практики не є можливим, тому доводиться використовувати наближені поправки. Під наближеною поправкою розумітимемо величину, додавши яку до результату вимірювання l отримаємо деяке наближене до Х значення y, тобто

Додавши наближену поправку до результату l_i отримаємо найймовірніше значення L, яке називається найймовірнішою поправкою, тобто

Графічна інтерпретація розглянутих|розглядувати| вище поправок ілюструється рис. 5.2 і рис. 5.3.

Рис. 5.2 – Ілюстрація зрівнювання результатів вимірів точною поправкою

Наступні|такі| властивості (властивість 4 і 5) арифметичної середини пов'язані з найймовірнішими| поправками.

Властивість 4. Якщо за ймовірніше значення вимірюваної величини прийнята арифметична середина, то сума найймовірніших поправок дорівнює нулю, тобто

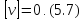
На підставі|основі| (5.6) запишемо наступну|таку| систему лінійних рівнянь

Отримані|одержувати| лінійні рівняння підсумуємо і запишемо їх, використовуючи символіку К.Ф. Гаусса

Порівнюючи рівняння (5.9) з перетвореним рівнянням простої арифметичної середини (5.1), а саме очевидно, що .

Властивість 5. Сума квадратів найймовірніших поправок, отриманих з арифметичної середини, завжди менша суми квадратів наближених поправок, отриманих для будь-якої іншої функції тих же результатів вимірів.

На підставі виразу|вираження| (5.5) і рис.5.3 запишемо систему лінійних рівнянь.

Рис. 5.3 – Ілюстрація зрівнювання результатів вимірів

| найймовірнішою поправкою

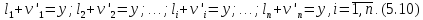
Віднімемо від|із| кожного рівняння отриманої|одержувати| системи лінійних рівнянь (5.10) рівняння системи (5.8) і, зробивши відповідні перетворення, отримаємо|одержуватимемо|:

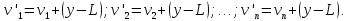
Піднесемо до квадрата праві і ліві частини|частки| отриманих|одержувати| рівнянь

Скориставшись формулами скороченого множення многочленів для квадратів, отримаємо

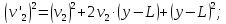|одержуватимемо|

...

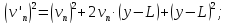
Підсумуємо отримані|одержувати| вирази і запишемо їх в символах К.Ф. Гаусса

У правій частині отриманої рівності середній доданок дорівнює нулю внаслідок того, що 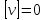(див. формулу 5.7). Тому

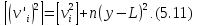
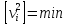Звідси випливає нерівність або яка і доводить сформульовану вище властивість.

Таким чином, розглянуті|розглядувати| властивості простої арифметичної середини є однією з основних характеристик оцінювання точності рівноточних| геодезичних вимірів|вимірів|. Знання властивостей простої арифметичної середини дозволяє правильно організувати математичну обробку рівноточних| геодезичних вимірів|вимірів|.