Додаткові джерела інформації

1. Бурмистров, Г.А. Теория математической обработки геодезических измерений [Текст]: пособие / Г.А. Бурмистров, В.Д.Большаков. – М.: Недра, 1969. – 400 с.

2. Войславский, Л.К. Теория математической обработки геодезических измерений. Часть 1. Теория погрешностей измерений [Текст] учебно-методическое пособие (для студентов 2 курса дневной формы обучения спец. 7.070908 «Геоинформационные системы и технологии») / Л.К. Войславский. – Х.: ХНАГХ, 2006. – 64 с.

3. Зазуляк, П.М. Основи математичного опрацювання геодезичних вимірів [Текст] навчальний посібник / П.М. Зазуляк, В.І. Гавриш, Е.М. Євсєєва, М.Д.Йосипчук. – Лвів: Видавництво «Растр-7», 2007. – 408 с.

4. Кемниц, Ю.В. Теория ошибок измерений [Текст]/ Ю.В.Кемниц. – М.: Недра, 1962. – 175 с.

6. Нерівноточні виміри

6.1. Вага як спеціальна міра відносної точності результатів нерівноточних| вимірів

Наближеними значеннями до стандарту є середня квадратична|з'являються| і емпірична середня квадратична| похибки вимірюваної величини. Вони ж є|з'являються| абсолютними кількісними мірами точності результатів вимірів|вимірів| і їх функцій. При зрівнюванні нерівноточних| вимірів|вимірів| виникає необхідність вводити спеціальну міру точності. Такою мірою є вага, формула обчислення|підрахунку| якої (2.15) наведена в п.п. 2.5. Розглянемо|розглядуватимемо| детально фізичний сенс|зміст| цього поняття.

Вага це спеціальна характеристика відносної точності вимірів і їх функцій, обчислена як величина, обернено пропорційна квадрату стандарта, тобто дисперсії результатів випадкових вимірів.

Якщо існує ряд нерівноточних результатів вимірів l₁, l₂,…, l_n точність яких характеризується стандартами σ₁, σ₂,…, σ_n відповідно, то ваги, що характеризують їх відносну точність, визначаються відношеннями

де с – загальний коефіцієнт пропорційності.

Звідси випливає, що вибір с із рівним квадрату стандарту σ_i² деякого результату виміри (реального або уявного) рівнозначний прийняттю ваги цього результату за одиницю.

Позначимо стандарт результату виміру, що має вагу, рівну одиниці символом .

Тоді рівняння (6.1) можна записати у наступному|слідуючому| вигляді|виді|:

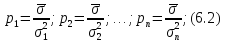
Величину 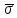прийнято називати стандартом одиниці ваги, а його наближені значення відповідно середньою квадратичною похибкою одиниці ваги і емпіричною середньою квадратичною похибкою одиниці ваги.

Як випливає з наведених вище міркувань і виразів (6.1) і (6.2), результати рівноточних вимірів, що мають однакові стандарти, тобто σ₁=σ₂=…=σ_n матимуть однакову вагу, яку можна прийняти рівною одиниці p₁=p₂=…=p_n=1.

Очевидно, що результати нерівноточних| вимірів|вимірів|, отримані|одержувати| за різних умов, матимуть нерівні ваги. Визначимо значення простої арифметичної середини L незалежних нерівноточних| результатів вимірів|вимірів|. Для цього зробимо наступні|такі| математичні перетворення. На підставі формальних співвідношень (6.1) запишемо пропорцію

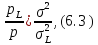
де σ – стандарт окремого виміру; σ_L – стандарт простої арифметичної середини.

Враховуючи результати обґрунтування другої властивості простої арифметичної середини, а саме формальні перетворення (5.3), можна записати

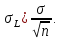
Підставляючи значення σ_L у пропорцію (6.3), отримаємо

Звідси випливає, що вага арифметичної середини незалежних нерівноточних| результатів вимірів|вимірів| в n разів більше ваги окремого результату.

Припустивши|передбачати|, що стандарт одиниці ваги дорівнює середній квадратичній| похибці одиниці ваги (див. формулу (6.2)), формула (6.4) набере вигляду

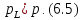
Таким чином, вага арифметичної середини незалежних результатів вимірів одиничної ваги дорівнює кількості цих результатів. При обробці результатів однорідних вимірів їх ваги є безрозмірними величинами. Якщо ж результати вимірів мають різну розмірність, наприклад, довжини лінії виміряні в метрах, а горизонтальні кути в секундах, то вага буде іменованою величиною