10.4. Оцінка точності зрівняних|урівнювати| значень невідомих геодезичних вимірів

Завершальною процедурою зрівнювання геодезичних вимірів параметричним способом, як це відомо|показний| із попереднього підрозділу, є оцінка точності зрівняних|урівнювати| значень невідомих. Розглянемо|розглядуватимемо| цю процедуру детально. Як і в математичній обробці однієї величини оцінюватимемо точність декількох невідомих, тобто визначимо їх середні квадратичні похибки| . Розв’язання даної задачі має деякі особливості, що полягають в тому, що поправки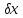, ,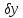, 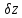…,, 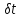– величини залежні. Причому математичному аналізу піддається не одна функція, а декілька.

Оскільки величини , ,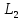…, 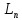(див. п.п. 10.1) виміряні|виміряти| незалежно і рівноточно|, їх середні квадратичні похибки| дорівнюють

.

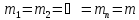Відповідно будуть рівні і їх ваги 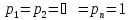, а також середні квадратичні похибки вимірівm і середні квадратичні похибки одиниць ваги μ, .

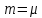Звернемося до рівняння (10.18), де елементи матриць Δ і λ є змінними, а елементами зворотної матриці є безперервні функції (10.10), що диференціюються, і відповідно до основної теореми теорії похибок (див. п.п.4.1) характеризуються стандартами даних функцій. Тоді зворотна матриця 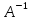може бути представлена функціональним визначником матриці Якобі (Якобіаном), елементи якого, є часткові похідні.

Запишемо:

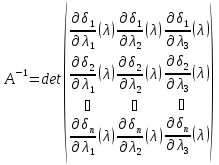. (10.19)

Підставимо отриману матрицю (10.19), а також матриці Δ і λ у вираз (10.18) і враховуючи властивості операцій над матрицями отримаємо наступне співвідношення:

.

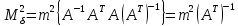Спрощуючи отриману|одержувати| формулу матимемо:

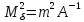. (10.20)

Отримана|одержувати| і записана в матричному вигляді формула для розрахунку середньої квадратичної похибки| сукупності поправок за умови рівноточних| вимірів і незалежності поправок , ,, …,.

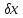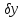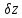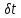Для обчислення точності зрівняних значень невідомих у разі їх залежності виконаємо наступні процедури. Враховуючи, що матриця 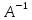симетрична, замінимо в ній діагональні елементи на вагові коефіцієнти, величини яких дорівнюють зворотним вагам невідомих

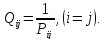
Відмітимо, що діагональні елементи формованої матриці Q завжди позитивні. Недіагональні елементи можуть бути як позитивними, так і негативними. Вони є кореляційними моментами, обумовленими залежністю певних невідомих. Наприклад, елемент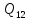і рівний йому елемент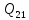слід розглядати як кореляційний момент, обумовлений залежністю величинx і у, тобто .

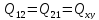Позитивне значення свідчить про те, що збільшення або зменшення похибки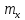неминуче приводить до збільшення або зменшення величини. І, навпаки, негативне значення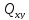свідчить про те, що збільшення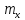тягне за собою зменшен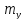ня, а зменшення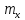– збільшення.

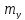Тоді справедливо записати, що, і 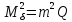. У розгорненому вигляді формула (10.20) набере вигляду

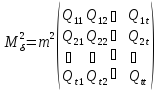. (10.21)

Звідси витікає, що квадрат середньої квадратичної похибки сукупності невідомих x, у, z,…, t є матрицею, яка отримана множенням квадрата середньої квадратичної похибки m виміряних величин 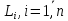на матрицюQ.

При обчисленні середніх квадратичних похибок невідомих x, у, z,…, t враховуватимемо, що ваги функцій результатів вимірів пов'язані із стандартом і стандартом одиниці ваги співвідношенням (6.8). Тоді справедливо записати наступні співвідношення:

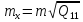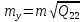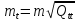, ,…,. (10.22)

З проведеного аналізу виходить, що хоча величини 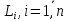виміряні рівноточно і незалежно, отримані в результаті зрівнювання значення незалежних величинx, у, z,…, t є нерівноточними і залежними величинами.

Приклад|зразок| 10.1.

Якщо шуканими невідомими є координати x, y пунктів геодезичної мережі, то сукупна похибка положення пункту в даній системі координат відповідно до виразу (10.21) характеризується матрицею:

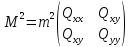. (10.23)

Отримана|одержувати| формула дає можливість|спроможність| розрахувати наступні точності| характеристики положення|становища| точки|точки| на площині|площині|:

1. Середні квадратичні похибки по осях координат 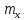і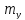, обчислювані за формулами (10.22). Вони залежать від вибору системи координат (рис. 10.1).

2. Кругову середню квадратичну похибку|, обчислювану за формулою:

, (10.24)

яка знайшла широке застосування|вживання| в геодезичній практиці, при цьому виходячи з припущення|гадки|, що розсіювання вимірів по осях X і Y має однакову ймовірність.

Рис. 10.1 – Ілюстрація для прикладу|приміром| 10.1

3. Еліпс похибок, орієнтація і розміри осей якого визначають найбільш вірогідні напрями|направлення| і величину максимальної і мінімальної середньої квадратичної похибки| положення геодезичного пункту.

Для визначення сукупної похибки положення геодезичного пункту скористаємося співвідношенням (10.23) і рис. 10.1, де показано, що поворотом осей навколо точки Р можна підібрати таку систему координат UV, при якій недіагональні елементи матриці Q дорівнюватимуть нулю і даний вираз матиме вигляд:

. (10.25)

Необхідний для такого перетворення кут|ріг| повороту осей обчислюється за формулою:

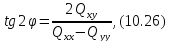
а елементи 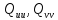на основі рівнянь:

.

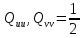
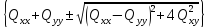Велика і мала піввісь еліпса похибок будуть відповідно дорівнювати:

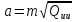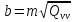, . (10.27)

Таким чином, детально розглянута|розглядувати| процедура (див. п.п.10.3 процедура 12) оцінювання точності зрівняних|урівнювати| значень невідомих. На прикладі|зразку| демонструється послідовність обчислення точнісних|підрахунку| |характеристик.