0 «Трикутник розподілу» Сімпсона р -1

Рис. 3.2 – Ілюстрація розподілу похибки округлень

на інтервалі вимірів [-0,5 – +0,5]

Як приклад|зразок| наведемо табл. 3.2, де в чисельному вигляді|виді| представлені|уявляти| співвідношення похибок округлення і ймовірність їх появи.

У геометричному нівелюванні перевищення на станції вимірюють|виміряють| двічі, за основною (чорною) і додатковою (червоною) сторонами рейки. За остаточний результат виміряного|виміряти| перевищення вважають середнє значення. Для середнього перевищення h можливо N=121²=14641 варіантів випадкової елементарної похибки округлення. Усю множину значень можна об'єднати в 21 інтервал групування, як це показано в правій частині|частці| табл. 3.2. За даними цієї таблиці побудуємо|спорудимо| криву розподілу випадкових похибок вимірів|вимірів| (рис. 3.3.), що виражає|виказує| деяку функцію f (Δ).

Таблиця 3.2 – Приклад|зразок| числових співвідношень ймовірності і величин

похибки округлення

Значення середини інтервалу	Діапазон значень в інтервалі	Обчислене|обчисляти| перевищення на станції			Середнє перевищення на станції
		Кількість випадків h	Вірогідність	Кількість випадків h		Вірогідність
1	2	3	4	5		6
- 1,0	-1,05 – -0,95	1	0,0083	3		0,002
- 0,9	-0,95 – -0,85	2	0,0165	22		0,0015
- 0,8	-0,85 – -0,75	3	0,0248	73		0,0050
- 0,7	-0,75 – -0,65	4	0,0331	172		0,0117
- 0,6	-0,65 – -0,55	5	0,0413	335		0,0229
- 0,5	-0,55 – -0,45	6	0,0496	576		0,0393
- 0,4	-0,45 – -0,35	7	0,0579	879		0,0600
- 0,3	-0,35 – -0,25	8	0,0661	1198		0,0818
- 0,2	-0,25 – -0,15	9	0,0744	1485		0,1014
- 0,1	-0,15 – -0,05	10	0,0826	1612		0,1156
0	-0,05 – +0,05	11	0,0909	1771		0,1210
+ 0,1	+0,05 – +0,15	10	0,0826	1692		0,1156
+ 0,2	+0,15 – +0,25	9	0,0744	1485		0,1014
+ 0,3	+0,25 – +0,35	8	0,0661	1198		0,0818
+ 0,4	+0,35 – +0,45	7	0,0579	879		0,0600
+ 0,5	+0,45 – +0,55	6	0,0496	576		0,0393
+ 0,6	+0,45 – +0,55	5	0,0413	335		0,0229
+ 0,7	+0,55 – +0,65	4	0,0331	172		0,0117
+ 0,8	+0,75 – +0,85	3	0,0248	73		0,0050
+ 0,9	+0,85 – +0,95	2	0,0165	22		0,0015
+ 1,0	+0,95 – +1,05	1	0,0083	3		0,0002
		121	1,0001	14641		0,9998

Відзначимо очевидні властивості цієї функції:

1. Функція завжди позитивна і симетрична щодо|відносно| осі ординат.

2. Функція має максимум у точці Δ = 0, де похідна функції f '(Δ) = 0.

3. Зі збільшенням абсолютної величини Δ функція f (Δ) асимптотично наближається до осі Δ.

4. Позитивним значенням Δ відповідають негативні|заперечні| значення f '(Δ), а негативним|заперечним| – позитивні значення f '(Δ), тобто має місце нерівність f '(Δ)·Δ < 0.

5. Представлені|уявляти| в правій частині|частці| табл. 3.2 ймовірності вичерпують усі можливі значення f (Δ). Отже, площа|майдан| фігури, обмежена віссю Δ і кривою має дорівнювати одиниці.

Перерахованим вище умовам відповідає функція, рівняння якої має вигляд:

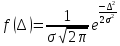(3.1)

Рис. 3.3 – Нормальний закон розподілу

Параметр σ в (3.1) визначає|уявляє| стандарт, який був викладений у попередньому підрозділі. Чим менше σ, тим тісніше групуються значення Δ щодо|відносно| осі f (Δ).

Розподіл випадкових похибок, представлений|уявляти| функцією (3.1), називають нормальним розподілом.

У розглянутому|розглядувати| вище прикладі|зразку| досліджувалося лише одне джерело формування випадкових похибок – похибок округлення відліку. Однак відомо, що на точність вимірювання|виміру| перевищення методом геометричного нівелювання окрім похибок округлення впливають також похибки, зумовлені випадковими коливаннями візирної осі приладу, коливаннями зображення рейки внаслідок|внаслідок| рефракції та інші чинники|факторами|.

Аналогічне явище має місце і в інших видах геодезичних вимірів|вимірах| – горизонтальних і вертикальних кутів|рогів| і напрямів|направлень|, довжин ліній і так далі. Усе це дає підставу|основу| розглядати|розглядувати| нормальний розподіл (3.1) як універсальний закон імовірнісного розподілу випадкових похибок.