11. Корелатний спосіб зрівнювання

11.1. Постановка задачі. Умовні рівняння

Вище (див. п.9.2) було відзначено, що існують два підходи до рішення задач зрівнювання систем виміряних геодезичних величин. Один з них параметричний спосіб, який викладено в п.10. Тепер розглянемо другий спосіб – зрівнювання виміряних величин, пов’язаних умовами (корелатний спосіб).

Ідея корелатного способу полягає в знаходженні поправок до виміряних величин через допоміжні невизначені множники, які називають корелатами. Сутність зрівнювання коре латним способом полягає в тому, що задачу знаходження мінімуму функції рівняння розкладеного в ряд Тейлора вирішують способом Лагранжа з визначенням корелат, у результаті чого отримують корелатні рівняння поправок (вектори поправок). Перетворивши рівняння поправок, отримують нормальні рівняння корелат, через які знаходять вірогідніші значення поправок.

Деталізуємо сказане і будемо вважати, що рівно точно виміряні n величин 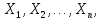пов’язаних незалежними математичними умовами

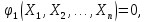
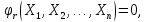(11.1)

де 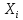,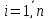–істинні значення виміряних величин.

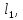
Загальна кількість таких умов дорівнює кількості надлишкових вимірів. Внаслідок неминучих похибок результати рівноточних вимірів 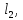…,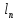небудуть точно задовольняти умовам (11.1). У результаті в правій частині системи рівнянь (11.1) справедливо записати деяку величину, яка відрізняється від нуля. Такі величини прийнято називати нев’язками, тобто

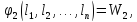
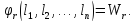(11.2)

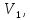
Сутність задачі полягає в тому, щоб знайти такі поправки 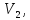…,до виміряних величин 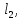…,,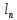які забезпечували б виконання умов (11.1), тобто

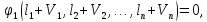
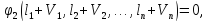
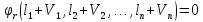(11.3)

Так як кількість невідомих в отриманій системі умовних рівнянь більша за кількість рівнянь, , товона не має однозначного розв’язання і є невизначеною.

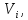
Для того щоб знайти поправки 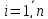,які найкращим чином зрівнювали б виміряні величин, скористаємося вже відомим методом найменших квадратів .

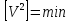Для цього необхідно привести умовні рівняння до лінійного вигляду, розклавши при цьому рівняння (11.3) в ряд Тейлора і обмежуючись при цьому першими членами ступеневого ряду, що мають степінь одиницю, отримаємо:

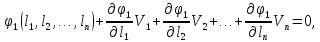
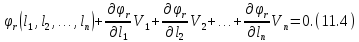
Введемо позначення, як це було зроблено в п.10.1 при постановці задачі зрівнювання поправок параметричним способом.

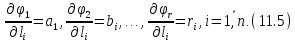
З урахуванням введених позначень (11.5), а також нев’язок, які є складовими перших частин системи рівнянь (11.2) представимо умовні рівняння в лінійному вигляді :

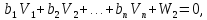
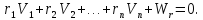
Або в матричному вигляді:

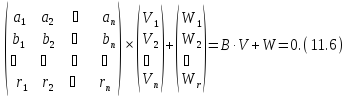
Таким чином, сформульована задача зрівнювання виміряних величин, пов’язаних умовами методом найменших квадратів, а також показаний шлях перетворення рівнянь до лінійного вигляду і представлення їх в матричному вигляді.

11.2. Знаходження умовного мінімуму методом найменших квадратів. Нормальні рівняння корелат і їх розв’язання

Система рівнянь (11.6) так само, як і система рівнянь (11.3) – невизначена 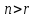. Її будемо розв’язувати методом найменших квадратів, тобто враховуючи умову 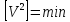.В курсі математичного аналізу доведено, що якщо є функція 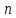змінних 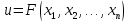,пов’язаних r додатковими умовами

,

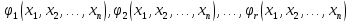причому 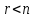,умовний екстремум функції u може бути знайдений методом, який запропонував Ж.Л. Лагранж.

Історична довідка

Використаємо доведення теореми Лагранжа. Для цього розглянемо функцію

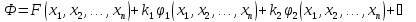
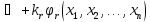, (11.7)

де 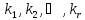–невизначені множники – корелати, які пов’язують між собою умовні змінні .

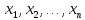Перетворимо функцію Ф в систему рівнянь, прирівнявши послідовно кожну складову формули (11.7) до нуля

,

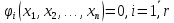а потім прирівняємо до нуля систему з 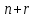рівнянь з невідомими. В скороченому вигляді можна записати:

.

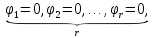
Для складання функції Лагранжа помножимо (11.6) на невизначені множники .Отримані вирази підсумуємо і додамо до функції .

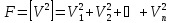В результаті математичних перетворень отримаємо функцію

.

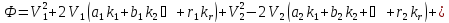
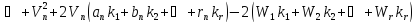Знайдемо локальні мінімуми в цій функції. Для цього візьмемо часткові похідні за змінними 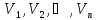і прирівняємо їх до нуля,

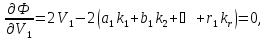
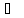
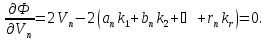
Із отриманої системи рівнянь знаходимо поправки ,,

,

,

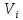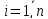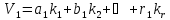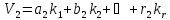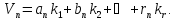
Представимо отриману систему рівнянь в матричному вигляді:

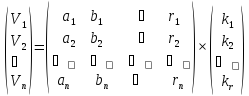
або в скороченому вигляді

(11.8)

Із отриманого співвідношення видно, що для обчислення поправок 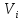до виміряних величин необхідно спочатку визначити матрицю К, яка являє собою вектор невизначених множників Лагранжа, тобто корелат …,

.

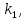
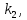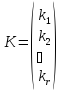Підставимо матрицю 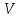із співвідношення (11.8) до формули (11.6) і отримаємо:

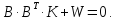(11.9)

Введемо позначення

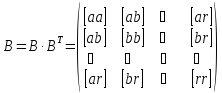. (11.10)

На підставі співвідношення (11.9) і введеного позначення (11.10) можна записати:

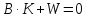. (11.11)

Отриманий вираз являє собою систему нормальних рівнянь, де кількість рівнянь r дорівнює кількості невідомих ,.

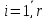Помножимо (11.10) слева на обратную матрицу 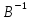, находим столбец коррелат

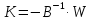. (11.12)

Підставимо значення матриці К у вираз (11.8), знайдемо стовпчик поправок V.

Контроль правильності перетворень здійснюють наступною процедурою. Помножимо вираз (11.8) зліва на транспоновану матрицю-рядок поправок 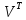.Отримаємо

.

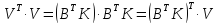Виконавши необхідні перетворення, знайдемо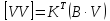, але так як 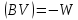, то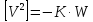,що і підтверджує правильність перетворень.

Упорядкуємо розглянуті вище математичні перетворення і задамо строгий порядок процедур зрівнювання виміряних величин, пов’язаних умовами.

Процедура 1. Визначення кількості і виду умовних рівнянь в системі виміряних геодезичних величин.

Процедура 2. Складання умовних рівнянь з нев’язками 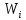,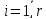та їх обчислення.

Процедура 3. Приведення отриманих рівнянь до лінійного вигляду шляхом розкладення їх у ряд Тейлора (11.4 -11.6).

Процедура 4. Складання матриці коефіцієнтів нормальних рівнянь корелат (11.10).

Процедура 5. Обчислення корелат 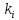,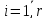з рівняння (11.11).

Процедура 6. Визначення вірогідніших поправок 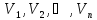підставленням корелат в рівняння (11.8).

Процедура 7. Контроль правильності виконаних математичних перетворень.

Таким чином, розглянута процедура знаходження умовного мінімуму методом найменших квадратів. Приведена послідовність розв’язання нормальних рівнянь корелат.